Bài 47. Lăng kính

Bài 4 trang 234 SGK Vật lí 11 Nâng cao

Khảo sát và vẽ

Đề bài

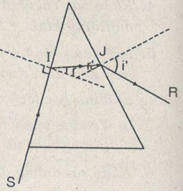
Khảo sát và vẽ đường di tia sáng trong trường hợp tia tới là là trên mặt lăng kính.

Lời giải chi tiết

Trong trường hợp tia tới là là trên mặt lăng kính, ta có góc tới \(i \approx {90^0}\) theo công thức sini = nsinr

\(\Rightarrow {\mathop{\rm s}\nolimits} {\rm{inr}} = {{\sin i} \over n} = {{\sin {{90}^0}} \over n} = {1 \over n}\)

\(\Rightarrow \) r bằng góc giới hạn của lăng kính \(\Rightarrow \) r = i_gh.

Góc tới r' = A - r = A - i_gh

Góc ló i': \(sini'{\rm{ }} = {\rm{ }}nsinr'{\rm{ }} = {\rm{ }}nsin\left( {A{\rm{ }} - {\rm{ }}r} \right){\rm{ }}\)

\(= > {\rm{ }}sin\left( {A{\rm{ }} - {\rm{ }}r} \right){\rm{ }} = {\rm{ }}{1 \over n}{\rm{ }}sini'\)

Dùng công thức lượng giác:

\(\sin A\cos r - \sin {\rm{rcosA = }}{{\sin i'} \over n}\)

\( \Leftrightarrow \sin A.\sqrt {1 - {\mathop{\rm s}\nolimits} {\rm{i}}{{\rm{n}}^2}{\rm{r}}} - \sin r\cos A = {{\sin i'} \over n}\)

\( \Leftrightarrow \sin A.\sqrt {1 - {1 \over {{n^2}}}} - {1 \over n}{\rm{cosA = }}{{\sin i'} \over n}\)

\( \Leftrightarrow \sin A.{{\sqrt {{n^2} - 1} } \over n} - {1 \over n}{\rm{cosA = }}{{\sin i'} \over n}\)

\( \Rightarrow \sin i' = \sin A.\sqrt {{n^2} - 1} - c{\rm{osA}}\)

Từ đây ta tìm dược góc i' và vẽ tia ló.

Loigiaihay.com

👉

Bình luận

Chia sẻ

Bình chọn:

3.5 trên 2 phiếu

>> Xem thêm

Báo lỗi - Góp ý

Các bài khác cùng chuyên mục

TẢI APP ĐỂ XEM OFFLINE