Giải toán 10, giải bài tập toán lớp 10 đầy đủ đại số và hình học
Bài 1. Giá trị lượng giác của một góc bất kỳ từ 0 độ đế..
Bài 4 trang 40 SGK Hình học 10
Chứng minh rằng với mọi góc alpha ta đều có:
Đề bài
Chứng minh rằng với mọi góc \(α \, (0^0≤ α ≤ 180^0)\) ta đều có \(\sin ^2\alpha + {\cos ^2}\alpha = 1.\)
Video hướng dẫn giải
Lời giải chi tiết
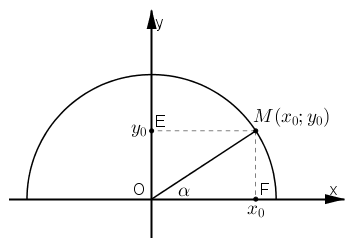
Vẽ nửa đường tròn đơn vị tâm O, bán kính 1 : (O; 1).
Lấy góc α bất kì (0º ≤ α ≤ 180º), luôn tồn tại điểm M(x0; y0) thuộc nửa đường tròn sao cho \(\widehat {xOM} = \alpha \)
Khi đó ta có: \(\sin \alpha = \frac{{MF}}{{OM}}= MF\) \(\cos \alpha = \frac{{OF}}{{OM}} = OF\); .
(\(OM = 1\) do \(M \in O\;(0,1)\)).
Ta có:
\({{{\sin }^2}\alpha + {{\cos }^2}\alpha = M{F^2} + O{F^2} = O{M^2} = {1^2} = 1}\)
\({ \Rightarrow {{\sin }^2}\alpha + {{\cos }^2}\alpha = 1}\)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 5 trang 40 SGK Hình học 10
- Bài 6 trang 40 SGK Hình học 10
- Bài 3 trang 40 SGK Hình học 10
- Bài 2 trang 40 SGK Hình học 10
- Bài 1 trang 40 SGK Hình học 10
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
