Toán 11, giải toán lớp 11 cánh diều Bài 1. Các số đặc trưng xu thế trung tâm cho mẫu số liệ..

Bài 3 trang 14 SGK Toán 11 tập 2 - Cánh Diều


Bảng 15 cho ta bảng tần số ghép nhóm số liệu thống kê chiều cao 40 mẫu cây

Đề bài

Bảng 15 cho ta bảng tần số ghép nhóm số liệu thống kê chiều cao 40 mẫu cây ở một vườn thực vật (đơn vị: centimet).

 

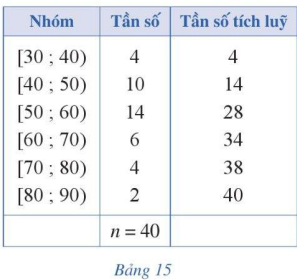
a) Xác định số trung bình cộng, trung vị, tứ phân vị của mẫu số liệu ghép nhóm trên.

b) Mốt của mẫu số liệu ghép nhóm trên là bao nhiêu?

Phương pháp giải - Xem chi tiết

- Áp dụng các công thức vừa được học để xác định các đại lượng tiêu biểu

Lời giải chi tiết

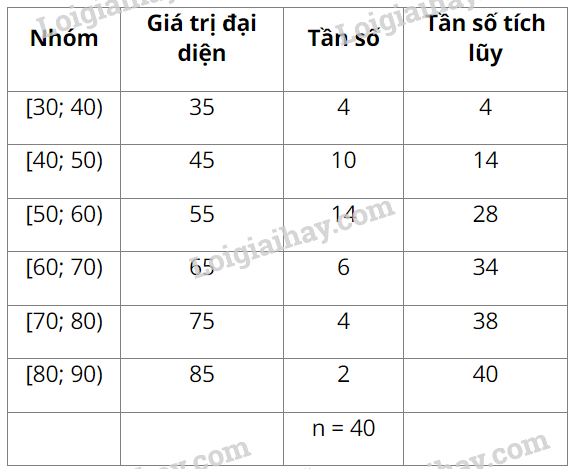
a) Số trung bình cộng của mẫu số liệu ghép nhóm đã cho là:

\(\overline x  = \frac{{35.4 + 45.10 + 55.14 + 65.6 + 75.4 + 85.2}}{{40}} = 55,5\)

⦁ Số phần tử của mẫu là n = 40. Ta có: \(\frac{n}{2} = \frac{{40}}{2} = 20\)

Mà \(14 < 20 < 28\) nên nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 20.

Xét nhóm 3 là nhóm \(\left[ {50;60} \right)\)có \(r = 50,d = 10,{n_3} = 14\) và nhóm 2 là nhóm \(\left[ {40;50} \right)\)có \(c{f_2} = 14\).

Áp dụng công thức, ta có trung vị của mẫu số liệu là:

\({M_e} = 50 + \frac{{20 - 14}}{{14}}.10 \approx 54,29\,(cm)\)

Do đó tứ phân vị thứ hai là \({Q_2} = {M_e} \approx 54,29\,\,(cm)\)

⦁ Ta có: \(\frac{n}{4} = \frac{{40}}{4} = 10\). Mà \(4 < 10 < 14\)nên nhóm 2 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 10.

Xét nhóm 2 là nhóm \(\left[ {40;50} \right)\)có \(s = 40,h = 10,{n_2} = 10\)và nhóm 1 là nhóm \(\left[ {30;40} \right)\)có \(c{f_1} = 4\).

Áp dụng công thức, ta có tứ phân vị thứ nhất là:

\({Q_1} = 40 + \frac{{10 - 4}}{{10}}.10 = 46\,(cm)\)

⦁ Ta có: \(\frac{{3n}}{4} = \frac{{3.40}}{4} = 30\). Mà \(28 < 30 < 34\)nên nhóm 4 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 30.

Xét nhóm 4 là nhóm \(\left[ {60;70} \right)\)có \(t = 60,l = 10,{n_4} = 6\)và nhóm 3 là nhóm \(\left[ {50;60} \right)\)có \(c{f_3} = 28\).

Áp dụng công thức, ta có tứ phân vị thứ ba là:

\({Q_3} = 60 + \frac{{30 - 28}}{6}.10 \approx 63,33\,(cm)\)

b) Nhóm 3 là nhóm \(\left[ {50;60} \right)\)có tần số lớn nhất với \(u = 50,g = 10,{n_3} = 14\)và nhóm 2 có tần số \({n_2} = 10\), nhóm 4 có tần số \({n_4} = 6\).

Áp dụng công thức, ta có mốt của mẫu số liệu là:

\({M_O} = 50 + \frac{{14 - 10}}{{2.14 - 10 - 6}}.10 \approx 53,33\,(cm)\)


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 11 - Cánh diều - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store