-
Toán 9 tập 1 - Cánh diều
-
Toán 9 tập 2 - Cánh diều
Toán 9 cánh diều | Giải toán lớp 9 cánh diều
Bài 4. Một số phép biến đổi căn thức bậc hai của biểu t..
Lý thuyết Một số phép biến đổi căn thức bậc hai của biểu thức đại số Toán 9 Cánh diều
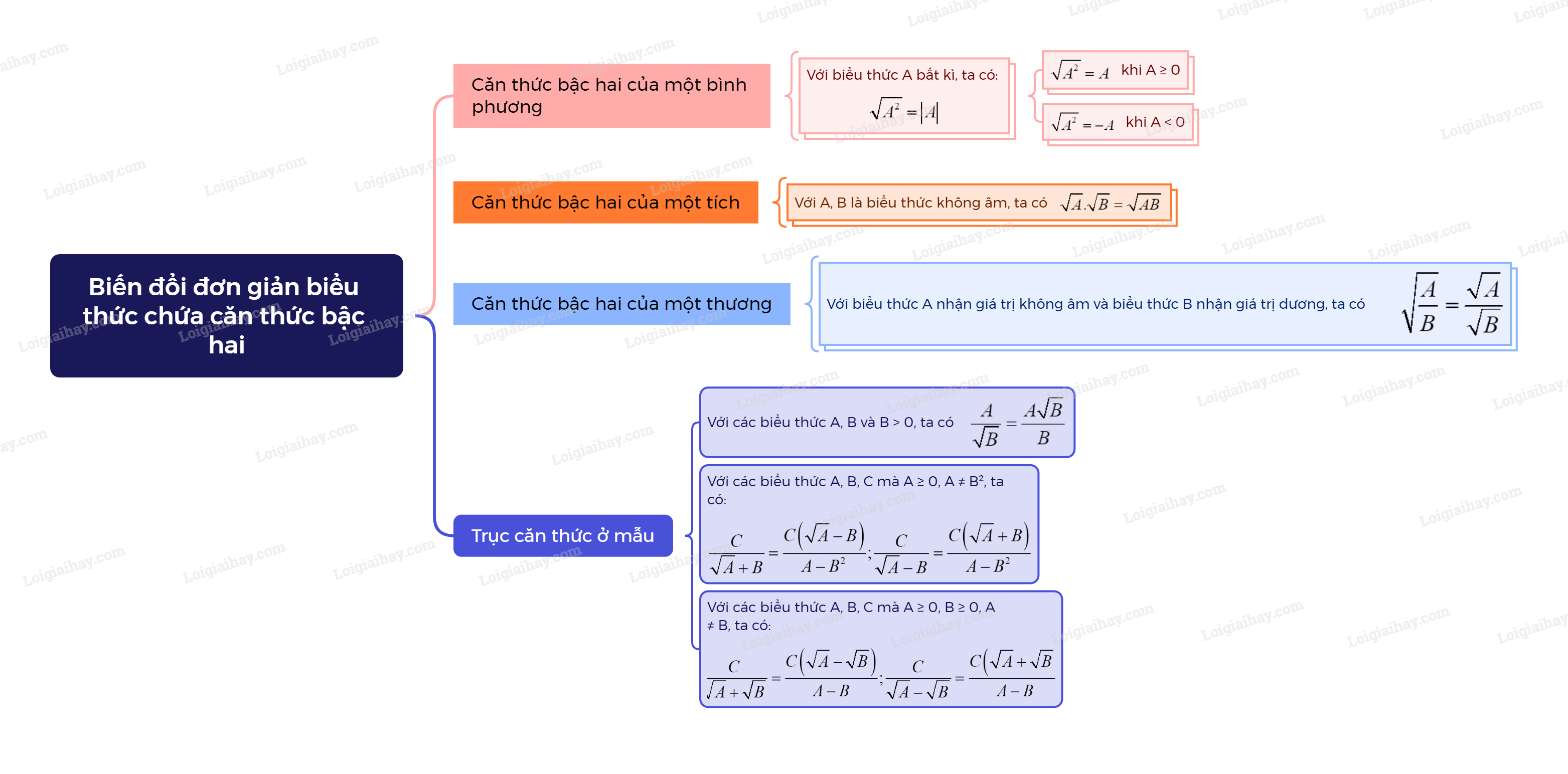
1. Căn thức bậc hai của một bình phương Quy tắc về căn thức bậc hai của một bình phương: Với mỗi biểu thức A, ta có: (sqrt {{A^2}} = left| A right|), tức là: (sqrt {{A^2}} = left| A right| = left{ begin{array}{l}A,khi,A ge 0\ - A,khi,A < 0end{array} right.)
Tổng hợp đề thi giữa kì 1 lớp 9 tất cả các môn - Cánh diều
Toán - Văn - Anh - Khoa học tự nhiên
1. Căn thức bậc hai của một bình phương
Quy tắc về căn thức bậc hai của một bình phương:
|
Với mỗi biểu thức A, ta có: \(\sqrt {{A^2}} = \left| A \right|\), tức là: \(\sqrt {{A^2}} = \left| A \right| = \left\{ \begin{array}{l}A\,khi\,A \ge 0\\ - A\,khi\,A < 0\end{array} \right.\) |
Ví dụ:\(\sqrt {{{\left( {x - 2} \right)}^2}} = \left| {x - 2} \right| = \left\{ \begin{array}{l}x - 2\,khi\,x \ge 2\\2 - x\,khi\,x \le 2\end{array} \right.\)
2. Căn thức bậc hai của một tích
Quy tắc về căn thức bậc hai của một tích:
|
Với các biểu thức A, B không âm, ta có: \(\sqrt {A.B} = \sqrt A .\sqrt B \). |
Ví dụ:
\(\sqrt {4{a^2}} = \sqrt 4 .\sqrt {{a^2}} = 2\left| a \right|\);
\(\sqrt {2a} .\sqrt {8a} = \sqrt {2a.8a} = \sqrt {16{a^2}} = \sqrt {16} .\sqrt {{a^2}} = 4\left| a \right|\).
3. Căn thức bậc hai của một thương
Quy tắc về căn bậc hai của một thương
|
Với các biểu thức A không âm và biểu thức B dương, ta có: \(\sqrt {\frac{A}{B}} = \frac{{\sqrt A }}{{\sqrt B }}\). |
Ví dụ:
\(\sqrt {\frac{{4{a^2}}}{{25}}} = \frac{{\sqrt {4{a^2}} }}{{\sqrt {25} }} = \frac{{2\left| a \right|}}{5}\);
\(\frac{{\sqrt {125a} }}{{\sqrt {5a} }} = \sqrt {\frac{{125a}}{{5a}}} = \sqrt {25} = 5\).
4. Trục căn thức ở mẫu
Nhận xét: Phép biến đổi làm mất căn thức bậc hai ở mẫu thức của một biểu thức được gọi là trục căn thức ở mẫu của biểu thức đó.
|
- Với các biểu thức A, B và B > 0, ta có \(\frac{A}{{\sqrt B }} = \frac{{A\sqrt B }}{B}\). - Với các biểu thức A, B, C mà \(B \ge 0,{A^2} \ne B\), ta có: \(\frac{C}{{A + \sqrt B }} = \frac{{C\left( {A - \sqrt B } \right)}}{{{A^2} - B}};\frac{C}{{A - \sqrt B }} = \frac{{C\left( {A + \sqrt B } \right)}}{{{A^2} - B}}\). (\(A - \sqrt B \) được gọi là biểu thức liên hợp của \(A + \sqrt B \) và ngược lại). - Với các biểu thức A, B, C mà \(A \ge 0,B \ge 0,A \ne B\), ta có: \(\frac{C}{{\sqrt A + \sqrt B }} = \frac{{C\left( {\sqrt A - \sqrt B } \right)}}{{A - B}};\frac{C}{{\sqrt A - \sqrt B }} = \frac{{C\left( {\sqrt A + \sqrt B } \right)}}{{A - B}}\). (\(\sqrt A - \sqrt B \) được gọi là biểu thức liên hợp của \(\sqrt A + \sqrt B \) và ngược lại). |
Ví dụ:
\(\frac{2}{{3\sqrt 5 }} = \frac{{2\sqrt 5 }}{{3{{\left( {\sqrt 5 } \right)}^2}}} = \frac{{2\sqrt 5 }}{{3.5}} = \frac{{2\sqrt 5 }}{{15}}\);
\(\frac{a}{{3 - 2\sqrt 2 }} = \frac{{a\left( {3 + 2\sqrt 2 } \right)}}{{\left( {3 - 2\sqrt 2 } \right).\left( {3 + 2\sqrt 2 } \right)}} = \frac{{a\left( {3 + 2\sqrt 2 } \right)}}{{{3^2} - {{\left( {2\sqrt 2 } \right)}^2}}} = \frac{{a\left( {3 + 2\sqrt 2 } \right)}}{{9 - 8}} = \left( {3 + 2\sqrt 2 } \right)a\).
Bình luận
Chia sẻ
- Giải câu hỏi khởi động trang 67 SGK Toán 9 tập 1 - Cánh diều
- Giải mục 1 trang 67 SGK Toán 9 tập 1 - Cánh diều
- Giải mục 2 trang 68 SGK Toán 9 tập 1 - Cánh diều
- Giải mục 3 trang 68, 69 SGK Toán 9 tập 1 - Cánh diều
- Giải mục 4 trang 69, 70 SGK Toán 9 tập 1 - Cánh diều
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 9 - Cánh diều - Xem ngay
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
