Lý thuyết Hàm số y = ax² (a ≠ 0) Toán 9 Cánh diều

1. Hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) Hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) xác định với mọi giá trị x thuộc \(\mathbb{R}\).

1. Hàm số \(y = a{x^2}\left( {a \ne 0} \right)\)

Hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) xác định với mọi giá trị x thuộc \(\mathbb{R}\).

Ví dụ: Hàm số \(y = 2{x^2},y = - \frac{3}{2}{x^2}\) là các hàm số có dạng \(y = a{x^2}\left( {a \ne 0} \right)\).

2. Đồ thị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\)

Đồ thị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\)

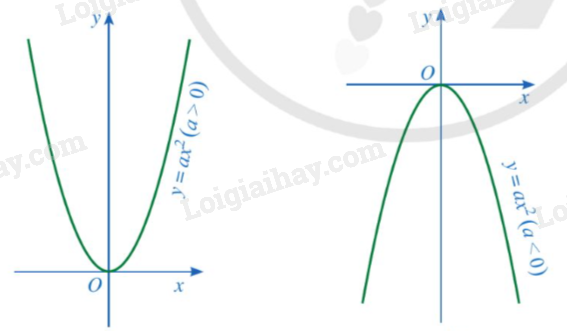
- Đồ thị của hàm số \(y = a{x^2}\) \(\left( {a \ne 0} \right)\) là một đường cong được gọi là parabol. Parabol đó luôn đi qua gốc tọa độ và có dạng như sau:

- Nếu a > 0 thì đồ thị đó nằm phía trên trục hoành.

- Nếu a < 0 thì đồ thị đó nằm phía dưới trục hoành.

Cách vẽ đồ thị hàm số \(y = a{x^2}\left( {a \ne 0} \right)\)

Bước 1. Lập bảng giá trị để tìm giá trị của y tương ứng với một số giá trị cụ thể của x.

Bước 2. Căn cứ vào bảng giá trị, về một số điểm cụ thể thuộc đồ thị của hàm số đó.

Bước 3. Vẽ parabol đi qua gốc tọa độ và các điểm đã xác định ở Bước 2, ta nhận được đồ thị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\).

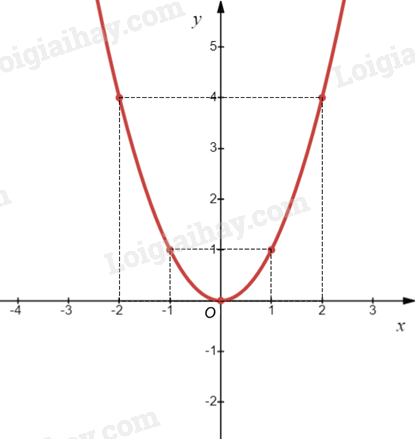
Ví dụ: Vẽ đồ thị của hàm số \(y = {x^2}\).

Bảng giá trị của hàm số:

Biểu diễn các điểm \(\left( { - 2;4} \right)\), \(\left( { - 1;1} \right)\), \(\left( {0;0} \right)\), \(\left( {1;1} \right)\), \(\left( {2;4} \right)\) trên mặt phẳng tọa độ Oxy và nối chúng lại với nhau, ta được đồ thị hàm số \(y = {x^2}\) như hình vẽ sau:

Tính chất

Đồ thị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) là một parabol đi qua gốc tọa độ và nhận trục Oy làm trục đối xứng.

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải mục 1 trang 46, 47 SGK Toán 9 tập 2 - Cánh diều
Xét hàm số (y = 5{x^2}) trong tình huống mở đầu. Hàm số có dạng (y = a{x^2}(a ne 0)) hay không? Nếu có, hãy xác định hệ số a của ({x^2}).
Giải mục 2 trang 49 SGK Toán 9 tập 2 - Cánh diều
a) Nêu khái niệm đồ thị của hàm số (y = f(x)). b) Xét hàm số (y = 2{x^2}). Hãy thực hiện các hoạt động sau: - Tìm giá trị của y tương ứng với giá trị của x trong bảng sau: - Trên mặt phẳng tọa độ Oxy, xác định các điểm có hoành độ và tung độ như trong bảng giá trị trên. - Quan sát Hình 1, vẽ đường cong như ở Hình 1 đi qua 5 điểm A, B, O, C, D. Đường cong đó được gọi là đường parabol và đường parabol đó là đồ thị của hàm số(y = 2{x^2}).
Giải bài tập 1 trang 51 SGK Toán 9 tập 2 - Cánh diều
Cho hàm số (y = a{x^2}). Tìm a, biết rằng khi (x = - 3) thì (y = 5).
Giải bài tập 2 trang 51 SGK Toán 9 tập 2 - Cánh diều
Cho hàm số (y = frac{1}{3}{x^2}). a) Tìm giá trị của y tương ứng với giái trị của x trong bảng sau: b) Dựa vào bảng giá trị trên, vẽ đồ thị của hàm số đó. c) Tìm những điểm thuộc đồ thị của hàm số có hoành độ lần lượt bằng -6; 10. d) Tìm những điểm thuộc đồ thị của hàm số có tung độ bằng 27.
Giải bài tập 3 trang 51 SGK Toán 9 tập 2 - Cánh diều
Trên mặt phẳng tọa độ Oxy, điểm M(2;-1) thuộc đồ thị hàm số (y = a{x^2}). a) Tìm hệ số a. b) Điểm A(4;-4) có thuộc đồ thị hàm số hay không? c) Hãy tìm một số điểm (không kể điểm O) thuộc đồ thị hàm số, rồi vẽ đồ thị của hàm số.
Giải bài tập 4 trang 51 SGK Toán 9 tập 2 - Cánh diều
Cho hàm số (y = a{t^2}) biểu thị quãng đường (đơn vị: mét) mà một chiếc xe đua đi được trong khoảng thời gian t (giây). Giả sử một chiếc xe đua đi được 125m sau khoảng thời gian là 5 giây. a) Tìm hệ số a. b) Vẽ đồ thị của hàm số.
Giải bài tập 5 trang 51 SGK Toán 9 tập 2 - Cánh diều
Cá heo có thể nhảy cao tới 25 feet và thực hiện các thủ thuật như nhảy qua vòng, lộn nhào trong không trung. Giả sử quỹ đạo nhảy của cá heo là parabol (y = a{x^2}), với gốc tọa độ là vị trí cao nhất mà cá heo đạt được, cách mặt nước 25 feet, trong đó y được tính theo đơn vị feet và x được tính theo đơn vị giây (Hình 6). Biết rằng sau 2 giây kể từ vị trí cao nhất đó, cá heo rơi chạm mặt nước. tìm hàm số biểu thị quỹ đạo nhảy của cá heo.