Toán 12 Cùng khám phá | Giải toán lớp 12 Cùng khám phá Bài 2. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số - ..

Lý thuyết Giá trị lớn nhất và giá trị nhỏ nhất của hàm số Toán 12 Cùng khám phá


1. Định nghĩa

1. Định nghĩa

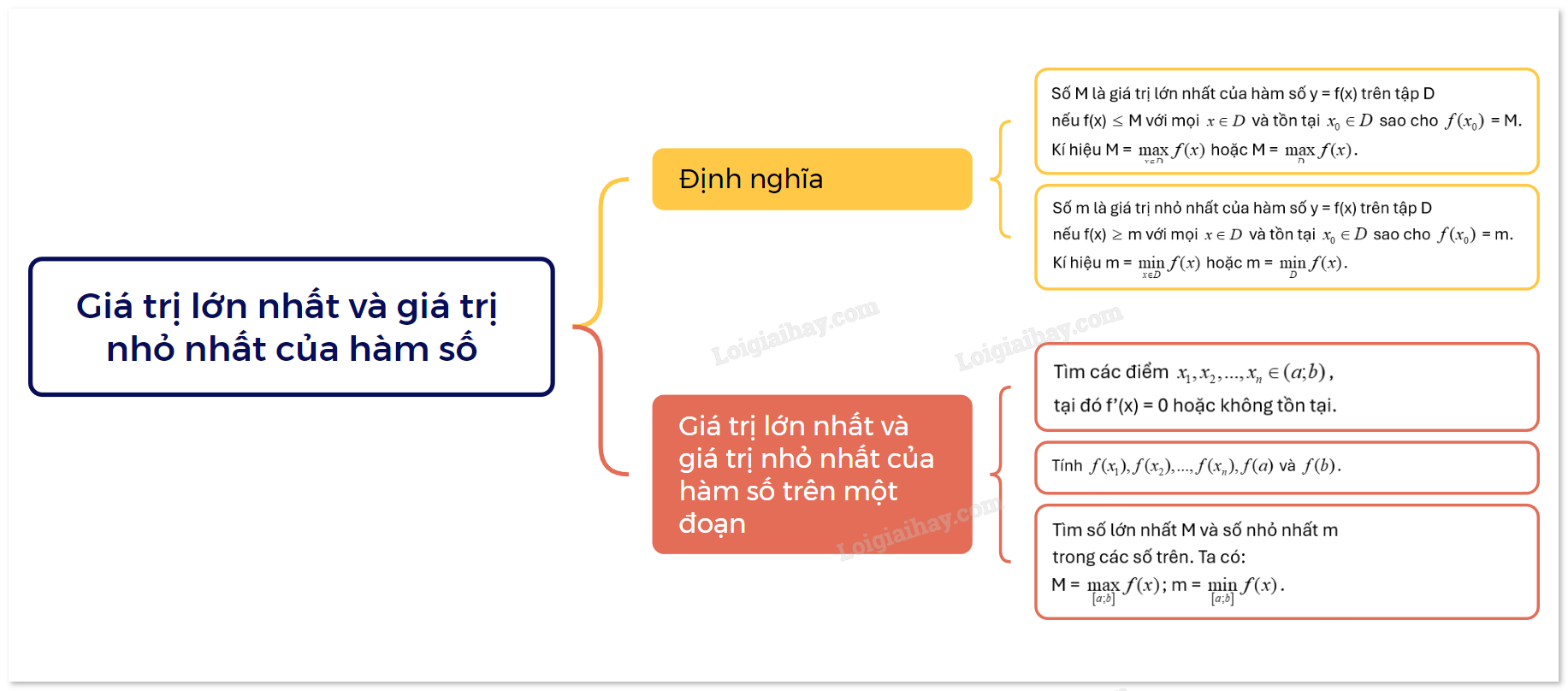
Cho hàm số y = f(x) xác định trên tập D.

+) Số M là giá trị lớn nhất của hàm số y = f(x) trên tập D nếu f(x) \( \le \) M với mọi \(x \in D\) và tồn tại \({x_0} \in D\) sao cho \(f({x_0})\) = M. Kí hiệu M = \(\mathop {\max }\limits_{x \in D} f(x)\) hoặc M = \(\mathop {\max }\limits_D f(x)\).

+) Số m là giá trị nhỏ nhất của hàm số y = f(x) trên tập D nếu f(x) \( \ge \) m với mọi \(x \in D\) và tồn tại \({x_0} \in D\) sao cho \(f({x_0})\) = m. Kí hiệu m = \(\mathop {\min }\limits_{x \in D} f(x)\) hoặc m = \(\mathop {\min }\limits_D f(x)\).

Ví dụ: Tìm GTLN, GTNN của hàm số \(y = f(x) = \sqrt {1 - {x^2}} \).

Tập xác định của hàm số là \(\left[ { - 1;1} \right]\).

Ta có:

  • \(f(x) = \sqrt {1 - {x^2}} \) \( \ge \) 0; dấu bằng xảy ra khi \(1 - {x^2} = 0\), tức x = -1 hoặc x = 1.

Do đó \(\mathop {\min }\limits_{x \in \left[ { - 1;1} \right]} f(x) = f( - 1) = f(1) = 0\).

  • \(f(x) = \sqrt {1 - {x^2}} \) \( \le 1\); dấu bằng xảy ra khi \(1 - {x^2} = 1\), tức x = 0.

Do đó \(\mathop {\max }\limits_{x \in \left[ { - 1;1} \right]} f(x) = f(0) = 1\).

2. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên một đoạn

Các bước tìm GTLN và GTNN của hàm số f(x) trên đoạn \(\left[ {a;b} \right]\):

  1. Tìm các điểm \({x_1},{x_2},...,{x_n} \in (a;b)\), tại đó f’(x) = 0 hoặc không tồn tại.
  2. Tính \(f({x_1}),f({x_2}),...,f({x_n}),f(a)\) và \(f(b)\).
  3. Tìm số lớn nhất M và số nhỏ nhất m trong các số trên. Ta có:
  4. M = \(\mathop {\max }\limits_{\left[ {a;b} \right]} f(x)\); m = \(\mathop {\min }\limits_{\left[ {a;b} \right]} f(x)\).

Ví dụ: Tìm GTLN và GTNN của hàm số \(y = {x^4} - 4{x^2} + 3\) trên đoạn \(\left[ {0;4} \right]\).

Ta có: \(y' = 4{x^3} - 8x = 4x({x^2} - 2);y' = 0 \Leftrightarrow x = 0\) hoặc \(x = \sqrt 2 \) (vì \(x \in \left[ {0;4} \right]\)).

y(0) = 3; y(4) = 195; y(\(\sqrt 2 \)) = -1.

Do đó: \(\mathop {\max }\limits_{\left[ {0;4} \right]} y = y(4) = 195\); \(\mathop {\min }\limits_{\left[ {0;4} \right]} y = y(\sqrt 2 ) =  - 1\).


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo
  • Giải mục 1 trang 10,11,12 SGK Toán 12 tập 1 - Cùng khám phá

    Định nghĩa

  • Giải mục 2 trang 12,13,14 SGK Toán 12 tập 1 - Cùng khám phá

    Giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên một đoạn

  • Giải bài tập 1.9 trang 14 SGK Toán 12 tập 1 - Cùng khám phá

    Cho hàm số \(y = f(x) = 3{x^4} - 16{x^3} + 18{x^2}\) có 1 phần đồ thị như hình 1.10. Tìm giá trị lớn nhất, giá trị nhỏ nhất( nếu có) đã cho trên: a) Nửa khoảng \(( - 1;4]\) b) Đoạn \([ - 1;1]\)

  • Giải bài tập 1.10 trang 14 SGK Toán 12 tập 1 - Cùng khám phá

    Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau a) \(y = f(x) = \frac{{{x^3}}}{3} + 2{x^2} + 3x - 4\) trên đoạn \([ - 4;1]\) b) \(y = f(x) = x + \frac{1}{x} - 2\) trên khoảng \(( - \infty ;0)\) c) \(y = f(x) = \frac{{x - 2}}{{2x - 3}}\)trên nửa khoảng \([2;6)\) d) \(y = f(x) = \sqrt {4 - {x^2}} \) e) \(y = f(x) = {e^x} - x\)trên đoạn \([ - 1;2]\) f) \(y = f(x) = x\ln x\)trên đoạn \([{e^{ - 2}};e]\)

  • Giải bài tập 1.11 trang 14 SGK Toán 12 tập 1 - Cùng khám phá

    Một thùng chứa nhiên liệu gồm một phần ở giữa là một hình trụ có chiều dài h mét( h>0)và 2 đầu là các nữa hình cầu bán kính r (r>0)(Hình 1.11). Biết rằng thể tích của thùng chứa là 144 000 \({m^3}\). Để sơn mắt ngoài phần hình cầu cần 20 000cho 1 \({m^2}\) , còn sơn phần ngoài phần hình trụ cần 10 000 đồng cho 1 \({m^2}\).Xác định r để chi phí cho việc sơn diện tích mắt ngoài thùng chứa( bao gồm diện tích xung quanh hình trụ và diện tích 2 nữa hình cầu) là nhỏ nhất, biết rằng bán kính r không đư

>> Xem thêm

Báo lỗi - Góp ý

Group Ôn Thi ĐGNL & ĐGTD Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store