Giải bài tập 1.11 trang 14 SGK Toán 12 tập 1 - Cùng khám phá

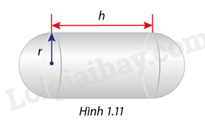
Một thùng chứa nhiên liệu gồm một phần ở giữa là một hình trụ có chiều dài h mét( h>0)và 2 đầu là các nữa hình cầu bán kính r (r>0)(Hình 1.11). Biết rằng thể tích của thùng chứa là 144 000 ({m^3}). Để sơn mắt ngoài phần hình cầu cần 20 000cho 1 ({m^2}) , còn sơn phần ngoài phần hình trụ cần 10 000 đồng cho 1 ({m^2}).Xác định r để chi phí cho việc sơn diện tích mắt ngoài thùng chứa( bao gồm diện tích xung quanh hình trụ và diện tích 2 nữa hình cầu) là nhỏ nhất, biết rằng bán kính r không đư

Đề bài

Một thùng chứa nhiên liệu gồm một phần ở giữa là một hình trụ có chiều dài h mét (h > 0) và 2 đầu là các nửa hình cầu bán kính r (r > 0) (Hình 1.11). Biết rằng thể tích của thùng chứa là 144 000 \({m^3}\). Để sơn mắt ngoài phần hình cầu cần 20 000 cho 1 \({m^2}\), còn sơn phần ngoài phần hình trụ cần 10 000 đồng cho 1 \({m^2}\). Xác định r để chi phí cho việc sơn diện tích mắt ngoài thùng chứa (bao gồm diện tích xung quanh hình trụ và diện tích 2 nửa hình cầu) là nhỏ nhất, biết rằng bán kính r không được vượt quá 50m.

Phương pháp giải - Xem chi tiết

Bước 1: Lập công thức tính chi phí sơn.

Bước 2: Lập bảng biến thiên của hàm số.

Bước 3: Tính chi phí nhỏ nhất để sơn là tìm giá trị nhỏ nhất của hàm số.

Quảng cáo

Lời giải chi tiết

Ta có thể tích thùng nhiên liệu là:

\(V = \frac{4}{3}{r^3}\pi + {r^2}\pi h \Leftrightarrow 144000\pi = \frac{4}{3}{r^3}\pi + {r^2}\pi h \Leftrightarrow h = \frac{{144000 - \frac{4}{3}{r^3}}}{{{r^2}}}\).

DIện tích xung quanh thùng nhiên liệu là là: \(S = 4{r^2}\pi + 2rh\pi \).

Số tiền cần để sơn xung quanh thùng nhiên liệu là:

\(T = 20000.4{r^2}\pi + 10000.2rh\pi = 80000{r^2}\pi + 20000rh\pi \left( {\frac{{144000 - \frac{4}{3}{r^3}}}{{{r^2}}}} \right)\)

\( = 80000{r^2}\pi + 2880000000\frac{\pi }{r} - \frac{{80000}}{3}{r^2}\pi = \frac{{160000}}{3}{r^2}\pi + 2880000000\frac{\pi }{r}\).

Bài toán trở thành tìm r để để hàm số T nhỏ nhất.

Ta có:

\(T' = \frac{{160000}}{3}\left( {2r} \right)\pi - 2880000000\frac{\pi }{{{r^2}}} = 0 \Leftrightarrow {r^3} = 27000 \Leftrightarrow r = 30\).

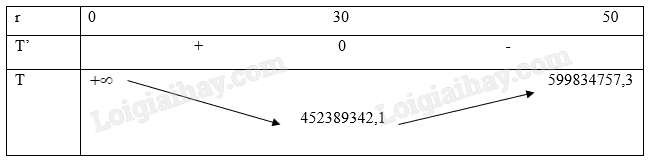
Vậy để chi phí sơn là nhỏ nhất thì r = 30.

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài tập 1.12 trang 14 SGK Toán 12 tập 1 - Cùng khám phá
Trong các hình chữ nhật có chu vi bằng 18cm. Hãy tìm hình chữ nhật có diện tích lớn nhất
Giải bài tập 1.13 trang 14 SGK Toán 12 tập 1 - Cùng khám phá
Một doạnh nghiệp tư nhân A chuyên kinh doanh xe gắn máy các loại. Hiện tại doạnh nghiệp đang tập trung vào chiến lược kinh doanh xe X với chi phi mua vào 27 triệu dộng và bán ra với giá 31 triệu đồng. với giá bán này, số lượng xe khách hàng đã mua trong 1 năm là 600 chiếc. Nhằm mục tiêu đẩy mạnh hơn nữa lượng tiêu thụ dòng xe đang bán chạy này, doanh nghiệp dự định sẽ giảm giá bán. Bộ phận nghiên cứu rằng nếu giảm 1 triệu đồng mỗi chiếu xe thì trong một năm số lượng xe bán ra trong một năm tăng
Giải bài tập 1.10 trang 14 SGK Toán 12 tập 1 - Cùng khám phá
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau a) \(y = f(x) = \frac{{{x^3}}}{3} + 2{x^2} + 3x - 4\) trên đoạn \([ - 4;1]\) b) \(y = f(x) = x + \frac{1}{x} - 2\) trên khoảng \(( - \infty ;0)\) c) \(y = f(x) = \frac{{x - 2}}{{2x - 3}}\)trên nửa khoảng \([2;6)\) d) \(y = f(x) = \sqrt {4 - {x^2}} \) e) \(y = f(x) = {e^x} - x\)trên đoạn \([ - 1;2]\) f) \(y = f(x) = x\ln x\)trên đoạn \([{e^{ - 2}};e]\)
Giải bài tập 1.9 trang 14 SGK Toán 12 tập 1 - Cùng khám phá
Cho hàm số \(y = f(x) = 3{x^4} - 16{x^3} + 18{x^2}\) có 1 phần đồ thị như hình 1.10. Tìm giá trị lớn nhất, giá trị nhỏ nhất( nếu có) đã cho trên: a) Nửa khoảng \(( - 1;4]\) b) Đoạn \([ - 1;1]\)
Giải mục 2 trang 12,13,14 SGK Toán 12 tập 1 - Cùng khám phá
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên một đoạn
Giải mục 1 trang 10,11,12 SGK Toán 12 tập 1 - Cùng khám phá
Định nghĩa
Lý thuyết Giá trị lớn nhất và giá trị nhỏ nhất của hàm số Toán 12 Cùng khám phá
1. Định nghĩa