 Toán 12 Cùng khám phá | Giải toán lớp 12 Cùng khám phá
Toán 12 Cùng khám phá | Giải toán lớp 12 Cùng khám phá
 Bài 2. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số - ..
Bài 2. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số - ..
Giải bài tập 1.12 trang 14 SGK Toán 12 tập 1 - Cùng khám phá
Trong các hình chữ nhật có chu vi bằng 18cm. Hãy tìm hình chữ nhật có diện tích lớn nhất
Đề bài
Trong các hình chữ nhật có chu vi bằng 18cm. Hãy tìm hình chữ nhật có diện tích lớn nhất
Phương pháp giải - Xem chi tiết
Bước 1: Lập công thức tính diện tích hình chữ nhật dưới dạng hàm số
Bước 2: Lập bảng biến thiên của hàm số
Bước 3: Tính diện tích lớn nhất của hình chữ nhật là tìm gía trị lớn nhất của hàm số
Lời giải chi tiết
Gọi x là chiều dài hình chữ nhật (0<x<9)
Khi đó chiều rộng hình chữ nhật là 9 - x ( > 0)
Diện tích hình chữ nhật là S(x) = x( 9 - x )
Ta có \({\rm{S'(x) = 9 - 2x}}\)
Xét \({\rm{S'(x) = 0}}\) \( \Rightarrow {\rm{x = }}\frac{{\rm{9}}}{{\rm{2}}}\)
Ta có bảng biến thiên là
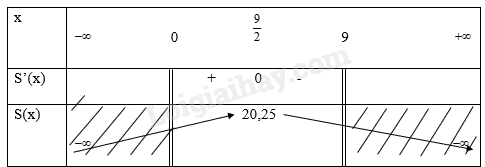
Vậy diện tích lớn nhất của hình chữ nhật là 20,25 khi chiều dài và chiều rộng bằng nhau và bằng \(\frac{{\rm{9}}}{{\rm{2}}}\)
- Giải bài tập 1.13 trang 14 SGK Toán 12 tập 1 - Cùng khám phá
- Giải bài tập 1.11 trang 14 SGK Toán 12 tập 1 - Cùng khám phá
- Giải bài tập 1.10 trang 14 SGK Toán 12 tập 1 - Cùng khám phá
- Giải bài tập 1.9 trang 14 SGK Toán 12 tập 1 - Cùng khám phá
- Giải mục 2 trang 12,13,14 SGK Toán 12 tập 1 - Cùng khám phá
>> Xem thêm
Các bài khác cùng chuyên mục
- Giải bài tập 6.20 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.19 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.18 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.17 trang 107 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.16 trang 107 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.20 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.19 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.18 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.17 trang 107 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.16 trang 107 SGK Toán 12 tập 2 - Cùng khám phá












Danh sách bình luận