-
Toán 9 tập 1 - Cùng khám phá
-
Toán 9 tập 2 - Cùng khám phá
Lý thuyết Bất đẳng thức Toán 9 Cùng khám phá
1. Bất đẳng thức Khi so sánh hai số thực a, b bất kì, luôn xảy ra một trong ba trường hợp sau:
1. Bất đẳng thức
Khi so sánh hai số thực a, b bất kì, luôn xảy ra một trong ba trường hợp sau:
- Số a bằng số b, kí hiệu \(a = b\);
- Số a lớn hơn số b, kí hiệu \(a > b\);
- Số a nhỏ hơn số b, kí hiệu \(a < b\).
Nếu số a không lớn hơn số b thì phải có hoặc \(a < b\), hoặc \(a = b\). Khi đó ta nói gọn là a nhỏ hơn hoặc bằng b và kí hiệu \(a \le b\).
Nếu số a không nhỏ hơn số b thì ta phải có hoặc \(a > b\), hoặc \(a = b\). Khi đó, ta nói a lớn hơn hoặc bằng b và kí hiệu \(a \ge b\).
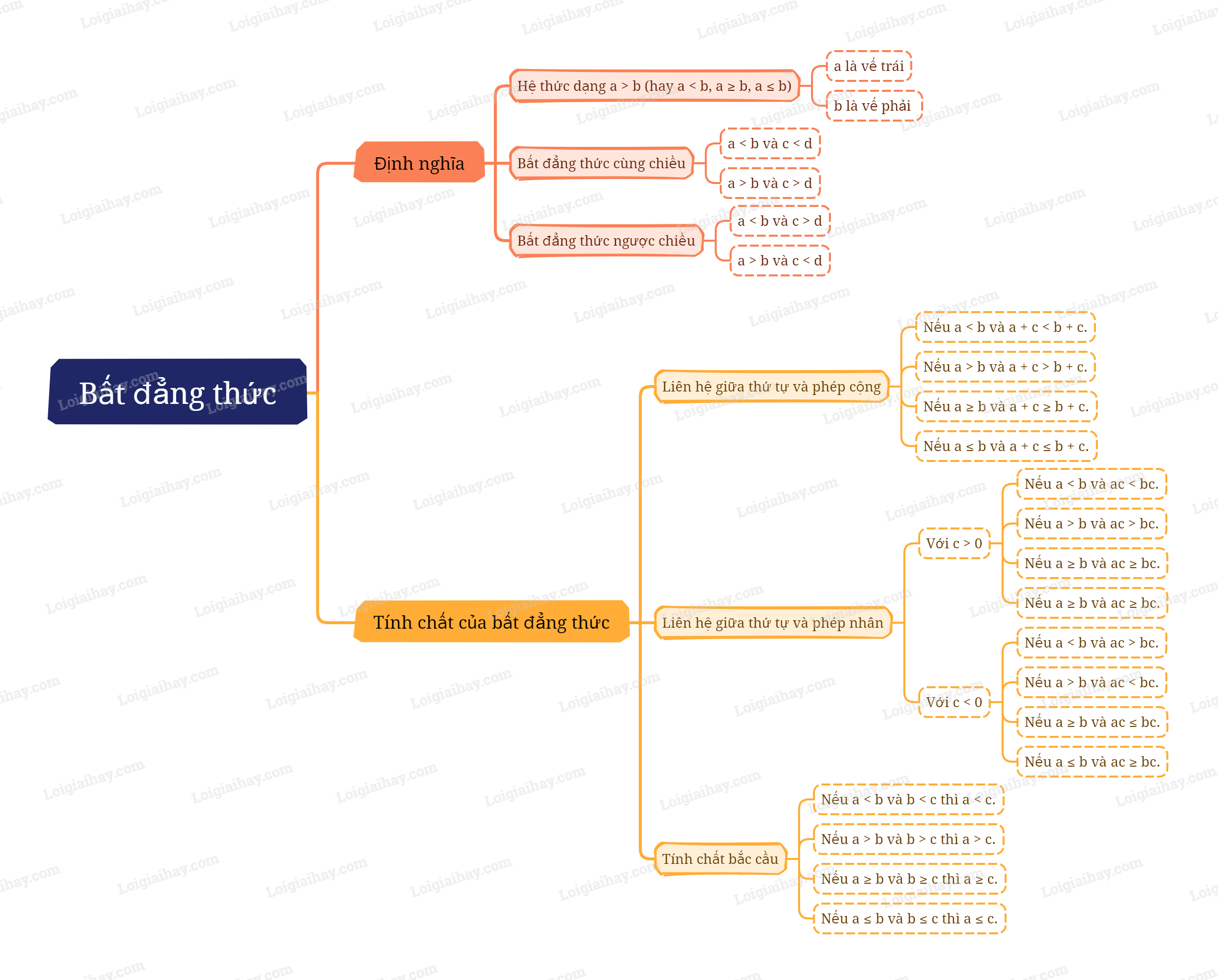
Định nghĩa bất đẳng thức
|
Hệ thức dạng \(a > b\) (hay \(a < b\), \(a \ge b\), \(a \le b\)) được gọi là bất đẳng thức. Khi đó a được gọi là vế trái và b được gọi là vế phải của bất đẳng thức. |
Lưu ý:
Bất đẳng thức a > b còn được viết là b < a.
Nếu đồng thời có hai bất đẳng thức a > b và a < c thì ta viết gộp lại thành b < a < c (đọc là a lớn hơn b, nhỏ hơn c)
Hai bất đẳng thức \(a > b\) và \(c > d\) (hay \(a \ge b\) và \(c \ge d\)) được gọi là hai bất đẳng thức cùng chiều.
Hai bất đẳng thức \(a > b\) và \(c < d\) (hay \(a \ge b\) và \(c \le d\)) được gọi là hai bất đẳng thức ngược chiều.
2. Liên hệ giữa thứ tự và phép cộng
Với ba số a, b, c, ta có:
|
Nếu \(a < b\) thì \(a + c < b + c\). Nếu \(a > b\) thì \(a + c > b + c\). Nếu \(a \le b\) thì \(a + c \le b + c\). Nếu \(a \ge b\) thì \(a + c \ge b + c\). Khi cộng cùng một số vào hai vế của bất đẳng thức, ta được bất đẳng thức mới cùng chiều với bất đẳng thức ban đầu. |
Ví dụ: Vì \(2023 < 2024\) nên \(2023 + \left( { - 19} \right) < 2024 + \left( { - 19} \right)\)
Lưu ý:
Tính chất trên vẫn đúng khi ta trừ vào hai vế của bất đẳng thức với cùng một số. Chẳng hạn, nếu \(a < b\) thì \(a - c < b - c\).
Ta có thể sử dụng tính chất trên để so sánh hai số hoặc chứng minh một bất đẳng thức.
3. Liên hệ giữa thứ tự và phép nhân
a) Liên hệ giữa thứ tự và phép nhân với số dương
|
Với ba số a, b, c bất kì, trong đó c > 0, ta có: - Nếu \(a < b\) thì \(ac < bc\). - Nếu \(a > b\) thì \(ac > bc\). - Nếu \(a \le b\) thì \(ac \le bc\). - Nếu \(a \ge b\) thì \(ac \ge bc\). Khi nhân cả hai vế của một bất đẳng thức với cùng một số dương, ta được bất đẳng thức mới cùng chiều với bất đẳng thức đã cho. |
Lưu ý:
Tính chất trên vẫn đúng khi ta chia hai vế của bất đẳng thức cho cùng một số dương.
Chẳng hạn, nếu \(a < b\) thì \(\frac{a}{c} < \frac{b}{c}\) với c là số dương bất kì.
b) Liên hệ giữa thứ tự và phép nhân với số âm
|
Với ba số a, b, c, trong đó c < 0, ta có: Nếu \(a < b\) thì \(ac > bc\). Nếu \(a > b\) thì \(ac < bc\). Nếu \(a \le b\) thì \(ac \ge bc\). Nếu \(a \ge b\) thì \(ac \le bc\). Khi nhân cả hai vế của một bất đẳng thức với cùng một số âm ta được bất đẳng thức mới ngược chiều với bất đẳng thức đã cho. |
Lưu ý:
Tính chất trên vẫn đúng khi ta chia hai vế của bất đẳng thức cho cùng một số âm.
Chẳng hạn, nếu \(a < b\) thì \(\frac{a}{c} > \frac{b}{c}\) với c là số âm bất kì.
Ví dụ:
Vì \( - 7 < - 5\) và \(3 > 0\) nên \(3.\left( { - 7} \right) < 3.\left( { - 5} \right)\).
Vì \( - 7 < - 5\) và \( - 3 < 0\) nên \(\left( { - 3} \right).\left( { - 7} \right) > \left( { - 3} \right).\left( { - 5} \right)\).
4. Tính chất bắc cầu của thứ tự
|
Nếu \(a < b\) và \(b < c\) thì \(a < c\). Tính chất này gọi là tính chất bắc cầu của thứ tự. |
Tính chất bắc cầu cũng đúng với các thứ tự lớn hơn (>), lớn hơn hoặc bằng (\( \ge \)), nhỏ hơn hoặc bằng (\( \le \)).
Ví dụ: Vì \(\frac{{2024}}{{2023}} = 1 + \frac{1}{{2023}} > 1\) và \(\frac{{2021}}{{2022}} = 1 - \frac{1}{{2022}} < 1\) nên \(\frac{{2024}}{{2023}} > \frac{{2021}}{{2022}}\).
Lưu ý:
Các tính chất của thứ tự cũng chính là tính chất của bất đẳng thức.
Bình luận
Chia sẻ
- Giải mục 1 trang 29, 30 SGK Toán 9 tập 1 - Cùng khám phá
- Giải mục 2 trang 31, 32 SGK Toán 9 tập 1 - Cùng khám phá
- Giải mục 3 trang 32, 33, 34 SGK Toán 9 tập 1 - Cùng khám phá
- Giải mục 4 trang 35 SGK Toán 9 tập 1 - Cùng khám phá
- Giải bài tập 2.1 trang 36 SGK Toán 9 tập 1 - Cùng khám phá
>> Xem thêm
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
Các bài khác cùng chuyên mục
- Lý thuyết Cách tính xác suất của biến cố trong một số mô hình đơn giản Toán 9 Cùng khám phá
- Lý thuyết Phép thử ngẫu nhiên. Không gian mẫu Toán 9 Cùng khám phá
- Lý thuyết Tần số ghép nhóm, tần số tương đối ghép nhóm Toán 9 Cùng khám phá
- Lý thuyết Tần số tương đối Toán 9 Cùng khám phá
- Lý thuyết Tần số Toán 9 Cùng khám phá
- Lý thuyết Cách tính xác suất của biến cố trong một số mô hình đơn giản Toán 9 Cùng khám phá
- Lý thuyết Phép thử ngẫu nhiên. Không gian mẫu Toán 9 Cùng khám phá
- Lý thuyết Tần số ghép nhóm, tần số tương đối ghép nhóm Toán 9 Cùng khám phá
- Lý thuyết Tần số tương đối Toán 9 Cùng khám phá
- Lý thuyết Tần số Toán 9 Cùng khám phá
