Copyright © 2021 loigiaihay.com
CHƯƠNG 1. SỐ HỮU TỈ
Bài 1. Tập hợp các số hữu tỉ
Bài 2. Cộng, trừ, nhân, chia số hữu tỉ
Luyện tập chung trang 14
Bài 3. Lũy thừa với số mũ tự nhiên của một số hữu tỉ
Bài 4. Thứ tự thực hiện các phép tính. Quy tắc chuyển vế
Luyện tập chung trang 23
Bài tập cuối chương 1
CHƯƠNG 2. SỐ THỰC
Bài 5. Làm quen với số thập phân vô hạn tuần hoàn
Bài 6. Số vô tỉ. Căn bậc hai số học
Bài 7. Tập hợp các số thực
Luyện tập chung trang 37
Bài tập cuối chương 2
CHƯƠNG 3. GÓC VÀ ĐƯỜNG THẲNG SONG SONG
Bài 8. Góc ở vị trí đặc biệt. Tia phân giác của một góc
Bài 9. Hai đường thẳng song song và dấu hiệu nhận biết
Luyện tập chung trang 50
Bài 10. Tiên đề Euclid. Tính chất của hai đường thẳng song song
Bài 11. Định lí và chứng minh định lí
Luyện tập chung trang 58
Bài tập cuối chương 3
CHƯƠNG 4. TAM GIÁC BẰNG NHAU
Bài 12. Tổng các góc trong một tam giác
Bài 13. Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác
Luyện tập chung trang 61
Bài 14. Trường hợp bằng nhau thứ hai và thứ ba của tam giác
Luyện tập chung trang 74
Bài 15. Các trường hợp bằng nhau của tam giác vuông
Bài 16. Tam giác cân. Đường trung trực của đoạn thẳng
Luyện tập chung trang 85
Bài tập cuối chương 4
CHƯƠNG 5. THU THẬP VÀ BIỂU DIỄN DỮ LIỆU
Bài 17. Thu thập và phân loại dữ liệu
Bài 18. Biểu đồ hình quạt tròn
Bài 19. Biểu đồ đoạn thẳng
Luyện tập chung trang 106
Bài tập cuối chương 5
HOẠT ĐỘNG THỰC HÀNH TRẢI NGHIỆM
Vẽ hình đơn giản với phần mềm GeoGebra
Dân số và cơ cấu dân số Việt Nam
Đại lượng tỉ lệ trong đời sống
CHƯƠNG 6. TỈ LỆ THỨC VÀ ĐẠI LƯỢNG TỈ LỆ
Bài 20. Tỉ lệ thức
Bài 21. Tính chất của dãy tỉ số bằng nhau
Luyện tập chung trang 10
Bài 22. Đại lượng tỉ lệ thuận
Bài 23. Đại lượng tỉ lệ nghịch
Luyện tập chung trang 19
Bài tập cuối chương 6
CHƯƠNG 7. BIỂU THỨC ĐẠI SỐ VÀ ĐA THỨC MỘT BIẾN
Bài 24. Biểu thức đại số
Bài 25. Đa thức một biến
Bài 26. Phép cộng và phép trừ đa thức một biến
Luyện tập chung trang 34
Bài 27. Phép nhân đa thức một biến
Bài 28. Phép chia đa thức một biến
Luyện tập chung trang 44
Bài tập cuối chương 7
CHƯƠNG 8. LÀM QUEN VỚI BIẾN CỐ VÀ XÁC SUẤT CỦA BIẾN CỐ
Bài 29. Làm quen với biến cố
Bài 30. Làm quen với xác suất của biến cố
Luyện tập chung trang 56
Bài tập cuối chương 8
CHƯƠNG 9. QUAN HỆ GIỮA CÁC YẾU TỐ TRONG TAM GIÁC
Bài 31. Quan hệ giữa góc và cạnh đối diện trong một tam giác
Bài 32. Quan hệ giữa đường vuông góc và đường xiên
Bài 33. Quan hệ giữa ba cạnh của một tam giác
Luyện tập chung trang 70
Bài 34. Sự đồng quy của ba đường trung tuyến, ba đường phân giác trong một tam giác
Bài 35. Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác
Luyện tập chung trang 82
Bài tập cuối chương 9
CHƯƠNG 10. MỘT SỐ HÌNH KHỐI TRONG THỰC TIỄN
Bài 36. Hình hộp chữ nhật và hình lập phương
Luyện tập trang 92
Bài 37. Hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác
Luyện tập trang 100
Bài tập cuối chương 10
ÔN TẬP CUỐI NĂM
Ôn tập cuối năm
Trắc nghiệm Tính số đo của một góc Toán 7 có đáp án
Trắc nghiệm Tính số đo của một góc
8 câu hỏi
Trắc nghiệm
Câu 1 :
Cho tam giác ABC có \(\widehat A = 86^\circ ;\widehat B = 62^\circ \). Số đo góc C là:
-
A.
\({32^0}\)
-
B.
\({35^0}\)
-
C.
\(24^\circ \)
-
D.
\({90^0}\)
-
A.
\({40^0}\)
-
B.
\({50^0}\)
-
C.
\({60^0}\)
-
D.
\({100^0}\)
Câu 3 :
Cho tam giác ABC có \(\widehat A = {50^0},\widehat B = {70^0}\). Tia phân giác của góc C cắt cạnh AB tại M. Số đo góc BMC là:
-
A.
\({50^0}\)
-
B.
\(80^\circ \)
-
C.
\({100^0}\)
-
D.
\({90^0}\)
Câu 4 :
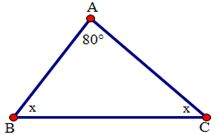
Tam giác ABC có \(\widehat A = {80^0},\widehat B - \widehat C = {50^0}\). Số đo góc B và góc C lần lượt là:
-
A.
\(\widehat B = {65^0},\widehat C = {15^0}\)
-
B.
\(\widehat B = {75^0},\widehat C = {25^0}\)
-
C.
\(\widehat B = {70^0},\widehat C = {20^0}\)
-
D.
\(\widehat B = {80^0},\widehat C = {30^0}\)
-
A.
\({40^0}\)
-
B.
\({50^0}\)
-
C.
\({60^0}\)
-
D.
\({70^0}\)
Câu 6 :
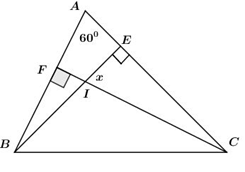
Cho hai đoạn thẳng AB và CD cắt nhau ở E. Các tia phân giác của các góc ACE và DBE cắt nhau ở K. Tính số đo góc BKC?
-
A.
90\(^\circ \)
-
B.
\(\widehat {BDC} - \widehat {BAC}\)
-
C.
\(\frac{{\widehat {BAC} + \widehat {BDC}}}{2}\)
-
D.
\(\widehat {BDC} + \widehat {BAC}\)
Câu 7 :
Tam giác ABC có \(\widehat B + \widehat C = \widehat A\) và \(\widehat C = 2\widehat B\). Tia phân giác của góc C cắt AB ở D. Tính \(\widehat {ADC}\)
-
A.
60\(^\circ \)
-
B.
90\(^\circ \)
-
C.
120\(^\circ \)
-
D.
30\(^\circ \)
-
A.
\({90^0}\)
-
B.
\({100^0}\)
-
C.
\({120^0}\)
-
D.
\({130^0}\)
CÁC BÀI TẬP KHÁC
