Toán 11, giải toán lớp 11 cánh diều Bài 6. Hình lăng trụ đứng. Hình chóp đều. Thể tích của ..

Giải mục 3 trang 112, 113, 114 SGK Toán 11 tập 2 - Cánh Diều


Hãy nêu lại công thức tính thể tích của khối lăng trụ đứng tam giác, khối lăng trụ đứng tứ giác.

Lựa chọn câu để xem lời giải nhanh hơn

Hoạt động 4

Hãy nêu lại công thức tính thể tích của khối lăng trụ đứng tam giác, khối lăng trụ đứng tứ giác. 

Phương pháp giải:

Nhớ lại công thức để nêu ra.

Lời giải chi tiết:

Thể tích của khối lăng trụ đứng tam giác, khối lăng trụ đứng tứ giác bằng diện tích đáy nhân với chiều cao.

V = B.h với B là diện tích đáy, h là chiều cao khối lăng trụ.

Luyện tập 4

Tính thể tích của khối lăng trụ \(ABC.A'B'C'\)' biết tất cả các cạnh bằng \(a\) và hình chiếu của \(A'\) trên mặt phẳng \(\left( {ABC} \right)\) là trung điểm của \(AB\).

Phương pháp giải:

Sử dụng công thức tính thể tích khối lăng trụ: \(V = Sh\).

Lời giải chi tiết:

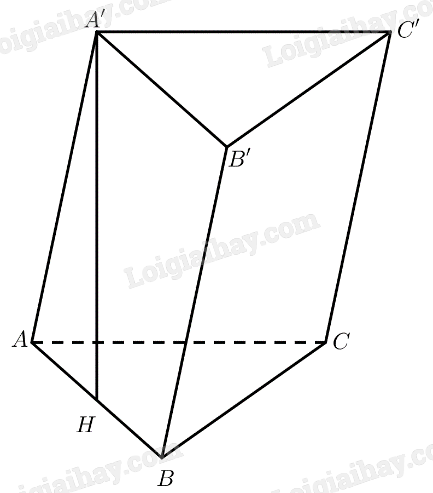
Gọi \(H\) là trung điểm của \(AB\)\( \Rightarrow A'H \bot \left( {ABC} \right)\)

\(AH = \frac{1}{2}AB = \frac{a}{2}\)

\(\Delta AA'H\) vuông tại \(H\)\( \Rightarrow A'H = \sqrt {AA{'^2} - A{H^2}}  = \frac{{a\sqrt 3 }}{2}\)

\(\begin{array}{l}{S_{\Delta ABC}} = \frac{{A{B^2}\sqrt 3 }}{4} = \frac{{{a^2}\sqrt 3 }}{4}\\{V_{ABC.A'B'C'}} = {S_{\Delta ABC}}.A'H = \frac{{3{a^3}}}{8}\end{array}\)

Luyện tập 5

Cho khối tứ diện đều \(ABCD\) cạnh \(a\). Chứng minh rằng thể tích của khối tứ diện đó bằng \(\frac{{{a^3}\sqrt 2 }}{{12}}\).

Phương pháp giải:

Sử dụng công thức tính thể tích khối chóp: \(V = \frac{1}{3}Sh\).

Lời giải chi tiết:

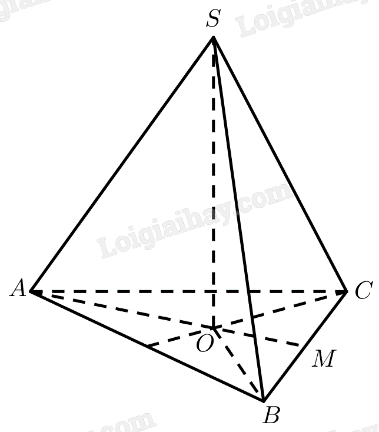
Gọi \(M\) là trung điểm của \(BC\), \(O\) là trọng tâm tam giác \(ABC\).

\( \Rightarrow SO \bot \left( {ABC} \right)\)

Tam giác \(ABC\) đều

\( \Rightarrow AM = \frac{{AB\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{2} \Rightarrow AO = \frac{2}{3}AM = \frac{{a\sqrt 3 }}{3}\)

Tam giác \(SAO\) vuông tại \(O \Rightarrow SO = \sqrt {S{A^2} - A{O^2}}  = \frac{{a\sqrt 6 }}{3}\)

\(\begin{array}{l}{S_{\Delta ABC}} = \frac{{A{B^2}\sqrt 3 }}{4} = \frac{{{a^2}\sqrt 3 }}{4}\\{V_{S.ABC}} = \frac{1}{3}{S_{\Delta ABC}}.SO = \frac{{{a^3}\sqrt 2 }}{{12}}\end{array}\)

Luyện tập 6

Một thùng đựng rác có dạng khối chóp cụt tứ giác đều với hai cạnh đáy lần lượt dài 2 dm và 3 dm, chiều cao bằng 4 dm. Tính thể tích của thùng đựng rác.

Phương pháp giải:

Sử dụng công thức tính thể tích khối chóp cụt đều: \(V = \frac{1}{3}h\left( {S + \sqrt {SS'}  + S'} \right)\).

Lời giải chi tiết:

Diện tích đáy lớn là: \(S = A{B^2} = {3^2} = 9\)

Diện tích đáy bé là: \(S' = {2^2} = 4\)

Thể tích hình chóp cụt là:

\(V = \frac{1}{3}h\left( {S + \sqrt {SS'}  + S'} \right) = \frac{1}{3}.4\left( {9 + \sqrt {9.4}  + 4} \right) = \frac{{76}}{3} \approx 25,3\left( {d{m^3}} \right)\)


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 11 - Cánh diều - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store