Giải mục 2 trang 9, 10, 11 SGK Toán 12 tập 1 - Kết nối tri thức

HĐ4

Trả lời câu hỏi Hoạt động 4 trang 9 SGK Toán 12 Kết nối tri thức

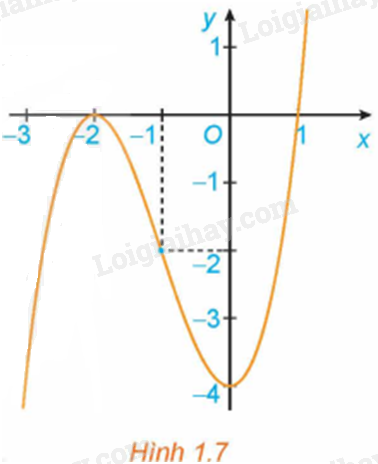
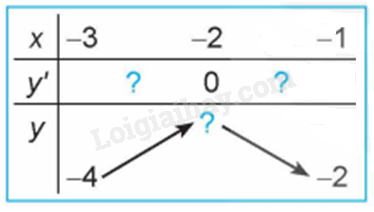
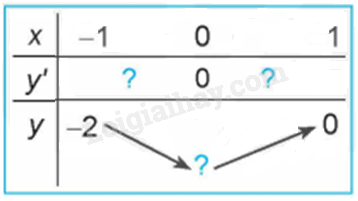
Quan sát đồ thị của hàm số \(y = {x^3} + 3{x^2} - 4\) (H.1.7). Xét dấu đạo hàm của hàm số đã cho và hoàn thành các bảng sau vào vở:

Phương pháp giải:

- Sử dụng kiến thức về định lí về tính đồng biến, nghịch biến của hàm số để tìm khoảng đồng biến, nghịch biến: Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên khoảng K.

+ Nếu \(f'\left( x \right) > 0\) với mọi \(x \in K\) thì hàm số \(f\left( x \right)\) đồng biến trên khoảng K.

+ Nếu \(f'\left( x \right) < 0\) với mọi \(x \in K\) thì hàm số \(f\left( x \right)\) nghịch biến trên khoảng K.

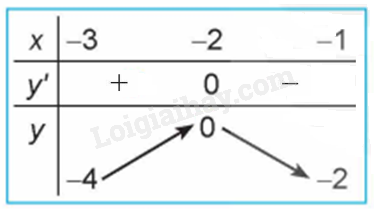
Lời giải chi tiết:

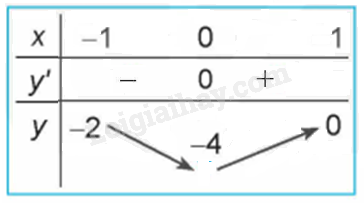
LT4

Trả lời câu hỏi Luyện tập 4 trang 10 SGK Toán 12 Kết nối tri thức

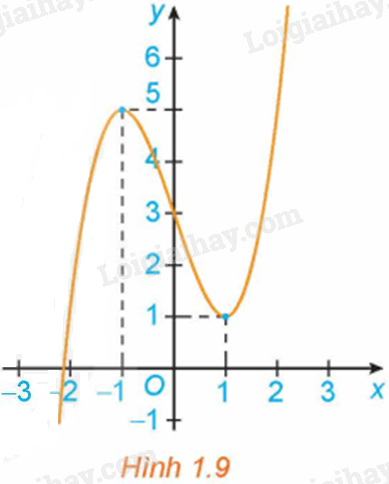
Hình 1.9 là đồ thị của hàm số \(y = f\left( x \right)\). Hãy tìm các cực trị của hàm số.

Phương pháp giải:

Sử dụng kiến thức về định nghĩa cực đại, cực tiểu của hàm số để tìm cực đại, cực tiểu của hàm số: Cho hàm số \(y = f\left( x \right)\) xác định và liên tục trên khoảng (a; b) (a có thể là \( - \infty \), b có thể là \( + \infty \)) và điểm \({x_0} \in \left( {a;b} \right)\).

+ Nếu tồn tại số \(h > 0\) sao cho \(f\left( x \right) < f\left( {{x_0}} \right)\) với mọi \(x \in \left( {{x_0} - h;{x_0} + h} \right) \subset \left( {a;b} \right)\) và \(x \ne {x_0}\) thì ta nói hàm số f(x) đạt cực đại tại \({x_0}\).

+ Nếu tồn tại số \(h > 0\) sao cho \(f\left( x \right) > f\left( {{x_0}} \right)\) với mọi \(x \in \left( {{x_0} - h;{x_0} + h} \right) \subset \left( {a;b} \right)\) và \(x \ne {x_0}\) thì ta nói hàm số f(x) đạt cực tiểu tại \({x_0}\).

Lời giải chi tiết:

Từ đồ thị hàm số, ta có:

Hàm số đạt cực tiểu tại \(x = 1\) và \({y_{CT}} = y\left( 1 \right) = 1\).

Hàm số đạt cực đại tại \(x =  - 1\) và \({y_{C{\rm{D}}}} = y( - 1) = 5\)      

HĐ5

Trả lời câu hỏi Hoạt động 5 trang 10 SGK Toán 12 Kết nối tri thức

Cho hàm số \(y = \frac{1}{3}{x^3} - 3{x^2} + 8x + 1\).

a) Tính đạo hàm \(f'\left( x \right)\) và tìm các điểm mà tại đó đạo hàm \(f'\left( x \right)\) bằng 0.

b) Lập bảng biến thiên của hàm số.

c) Từ bảng biến thiên suy ra các điểm cực trị của hàm số.

Phương pháp giải:

Sử dụng kiến thức về định nghĩa cực đại, cực tiểu của hàm số để tìm cực đại, cực tiểu của hàm số: Cho hàm số \(y = f\left( x \right)\) xác định và liên tục trên khoảng (a; b) (a có thể là \( - \infty \), b có thể là \( + \infty \)) và điểm \({x_0} \in \left( {a;b} \right)\).

+ Nếu tồn tại số \(h > 0\) sao cho \(f\left( x \right) < f\left( {{x_0}} \right)\) với mọi \(x \in \left( {{x_0} - h;{x_0} + h} \right) \subset \left( {a;b} \right)\) và \(x \ne {x_0}\) thì ta nói hàm số f(x) đạt cực đại tại \({x_0}\).

+ Nếu tồn tại số \(h > 0\) sao cho \(f\left( x \right) > f\left( {{x_0}} \right)\) với mọi \(x \in \left( {{x_0} - h;{x_0} + h} \right) \subset \left( {a;b} \right)\) và \(x \ne {x_0}\) thì ta nói hàm số f(x) đạt cực tiểu tại \({x_0}\).

Lời giải chi tiết:

a) Tập xác định: \(D = \mathbb{R}\).

\(y' = {x^2} - 6x + 8\), \(y' = 0 \Leftrightarrow {x^2} - 6x + 8 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 4\\x = 2\end{array} \right.\)

Vậy \(x = 4;x = 2\) thì \(f'\left( x \right) = 0\)

b) Bảng biến thiên:

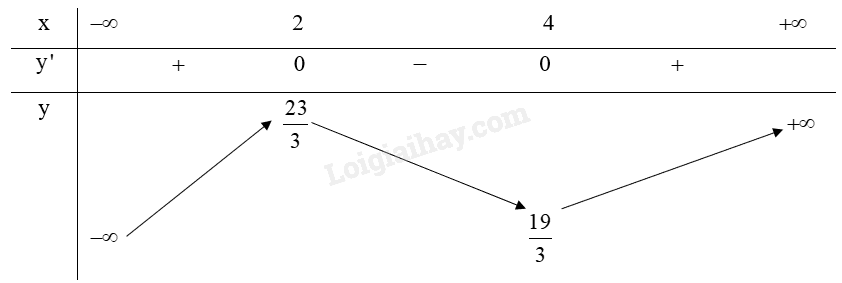
c) Từ bảng biến thiên ta có:

Hàm số \(y = \frac{1}{3}{x^3} - 3{x^2} + 8x + 1\) có điểm cực đại là \(\left( {2;\frac{{23}}{3}} \right)\).

Hàm số \(y = \frac{1}{3}{x^3} - 3{x^2} + 8x + 1\) có điểm cực tiểu là \(\left( {4;\frac{{19}}{3}} \right)\). 

CH

Trả lời câu hỏi trang 11 SGK Toán 12 Kết nối tri thức

Giải thích vì sao nếu f’(x) không đổi dấu qua \({x_0}\) thì \({x_0}\) không phải là điểm cực trị của hàm số f(x)?

Phương pháp giải:

Sử dụng kiến thức về định lí cực trị hàm số để chứng minh: Giả sử hàm số \(y = f\left( x \right)\) liên tục trên khoảng (a; b) chứa điểm \({x_0}\) và có đạo hàm trên các khoảng \(\left( {a;{x_0}} \right)\) và \(\left( {{x_0};b} \right)\). Khi đó:

+ Nếu \(f'\left( x \right) < 0\) với mọi \(x \in \left( {a;{x_0}} \right)\) và \(f'\left( x \right) > 0\) với mọi \(x \in \left( {{x_0};b} \right)\) thì điểm \({x_0}\) là một điểm cực tiểu của hàm số f(x).

+ Nếu \(f'\left( x \right) > 0\) với mọi \(x \in \left( {a;{x_0}} \right)\) và \(f'\left( x \right) < 0\) với mọi \(x \in \left( {{x_0};b} \right)\) thì điểm \({x_0}\) là một điểm cực đại của hàm số f(x).d

Lời giải chi tiết:

Giả sử hàm số \(y = f\left( x \right)\) liên tục trên khoảng (a; b) chứa điểm \({x_0}\) và có đạo hàm trên các khoảng \(\left( {a;{x_0}} \right)\) và \(\left( {{x_0};b} \right)\). Nếu f’(x) không đổi dấu qua \({x_0}\) thì:

TH1: \(f'\left( x \right) < 0\) với mọi \(x \in \left( {a;{x_0}} \right)\) và \(f'\left( x \right) < 0\) với mọi \(x \in \left( {{x_0};b} \right)\), ta có bảng biến thiên:

Giả sử hàm số \(y = f\left( x \right)\) liên tục trên khoảng (a; b) chứa điểm \({x_0}\) và có đạo hàm trên các khoảng \(\left( {a;{x_0}} \right)\) và \(\left( {{x_0};b} \right)\). Nếu f’(x) không đổi dấu qua \({x_0}\) thì:

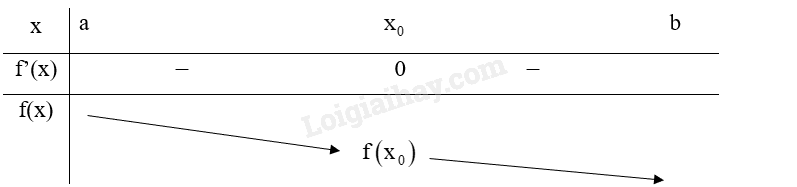
TH1: \(f'\left( x \right) < 0\) với mọi \(x \in \left( {a;{x_0}} \right)\) và \(f'\left( x \right) < 0\) với mọi \(x \in \left( {{x_0};b} \right)\), ta có bảng biến thiên:

Do đó, \({x_0}\) không phải là điểm cực trị của hàm số f(x).

LT5

Trả lời câu hỏi Luyện tập 5 trang 12 SGK Toán 12 Kết nối tri thức

Tìm cực trị của các hàm số sau:

a) \(y = {x^4} - 3{x^2} + 1\);                                            

b) \(y = \frac{{ - {x^2} + 2x - 1}}{{x + 2}}\).

Phương pháp giải:

Sử dụng kiến thức về cách tìm cực trị của hàm số \(y = f\left( x \right)\) để tìm cực trị của hàm số:

1. Tìm tập xác định của hàm số.

2. Tính đạo hàm f’(x). Tìm các điểm mà tại đó đạo hàm f’(x) bằng 0 hoặc đạo hàm không tồn tại.

3. Lập bảng biến thiên của hàm số.

4. Từ bảng biến thiên suy ra các cực trị của hàm số.

Lời giải chi tiết:

a) Tập xác định của hàm số là \(\mathbb{R}\).

Ta có: \(y' = 4{x^3} - 6x,y' = 0 \Leftrightarrow 4{x^3} - 6x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x =  \pm \frac{{\sqrt 6 }}{2}\end{array} \right.\);

Bảng biến thiên:

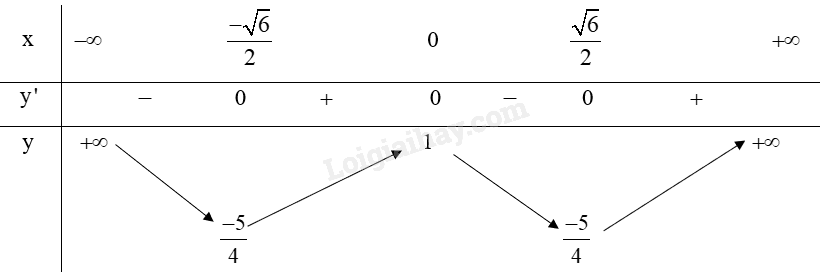
Từ bảng biến thiên ta có:

Hàm số đạt cực đại tại \(x = 0\) và .

Hàm số đạt cực tiểu tại \(x =  \pm \frac{{\sqrt 6 }}{2}\) và \({y_{CT}} = \frac{{ - 5}}{4}\).

b) Tập xác định: \(D = \mathbb{R}\backslash \left\{ { - 2} \right\}\).

Ta có: \(y' = \frac{{\left( { - 2x + 2} \right)\left( {x + 2} \right) - \left( { - {x^2} + 2x - 1} \right)}}{{{{\left( {x + 2} \right)}^2}}} = \frac{{ - {x^2} - 4x + 5}}{{{{\left( {x + 2} \right)}^2}}}\)

\(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x =  - 5\\x = 1\end{array} \right.\) (thỏa mãn)

Lập bảng biến thiên của hàm số:

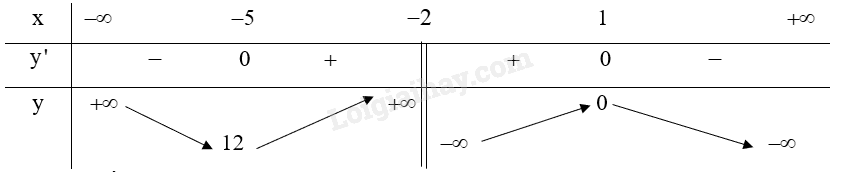
Từ bảng biến thiên ta có:

Hàm số đạt cực đại tại \(x = 1\) và .

Hàm số đạt cực tiểu tại \(x =  - 5\) và \({y_{CT}} = 12\).

VD2

Trả lời câu hỏi Vận dụng 2 trang 12 SGK Toán 12 Kết nối tri thức

Một vật được phóng thẳng đứng lên trên từ độ cao 2m với vận tốc ban đầu là 24,5m/s. Trong Vật lí, ta biết rằng khi bỏ qua sức cản của không khí thì độ cao h (mét) của vật sau t (giây) được cho bởi công thức: \(h\left( t \right) = 2 + 24,5t - 4,9{t^2}\). Hỏi tại thời điểm nào thì vật đạt độ cao lớn nhất?

Phương pháp giải:

Sử dụng kiến thức về cách tìm cực trị của hàm số \(y = f\left( x \right)\) để tìm thời điểm vật đạt độ cao lớn nhất:

1. Tìm tập xác định của hàm số.

2. Tính đạo hàm f’(x). Tìm các điểm mà tại đó đạo hàm f’(x) bằng 0 hoặc đạo hàm không tồn tại.

3. Lập bảng biến thiên của hàm số.

4. Từ bảng biến thiên suy ra các cực trị của hàm số.

Lời giải chi tiết:

Xét hàm số: \(h\left( t \right) = 2 + 24,5t - 4,9{t^2}\).

Tập xác định của hàm số là \(\mathbb{R}\).

Ta có: \[h'\left( t \right) =  - 9,8t + 24,5;h'\left( t \right) = 0 \Leftrightarrow  - 9,8t + 24,5 = 0 \Leftrightarrow t = \frac{5}{2}\].

Bảng biến thiên:

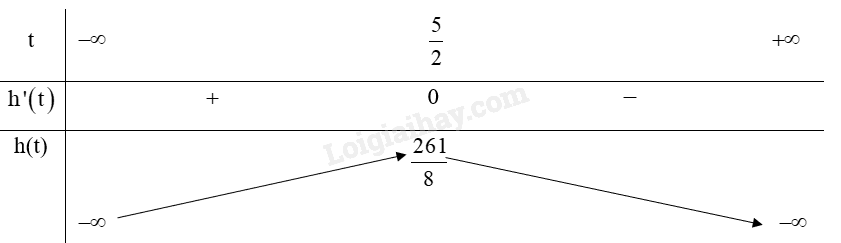
Từ bảng biến thiên ta có:

Hàm số đạt cực đại tại \(t = \frac{5}{2}\),

Vậy thời điểm vật đạt độ cao lớn nhất là \(t = \frac{5}{2}\) giây