Giải mục 1 trang 5,6,7 SGK Toán 12 tập 1 - Kết nối tri thức

HĐ1

Trả lời câu hỏi Hoạt động 1 trang 6 SGK Toán 12 Kết nối tri thức

Quan sát đồ thị của hàm số \(y = {x^2}\)  (H.1.2)

a) Hàm số đồng biến trên khoảng nào?

b) Hàm số nghịch biến trên khoảng nào?

Phương pháp giải:

Sử dụng kiến thức về tính đồng biến, nghịch biến của hàm số để tìm khoảng đồng biến, nghịch biến: Giả sử K là một khoảng, một đoạn hoặc một nửa khoảng và \(y = f\left( x \right)\) là hàm số xác định trên K.

+ Hàm số \(y = f\left( x \right)\) được gọi là đồng biến trên K nếu \(\forall {x_1},{x_2} \in K,{x_1} < {x_2} \Rightarrow f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\)

+ Hàm số \(y = f\left( x \right)\) được gọi là nghịch biến trên K nếu \(\forall {x_1},{x_2} \in K,{x_1} < {x_2} \Rightarrow f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\)

Lời giải chi tiết:

Từ đồ thị ta thấy:

+ Xét khoảng \(\left( {0; + \infty } \right)\): \(\forall {x_1},{x_2} \in \left( {0; + \infty } \right),{x_1} < {x_2}\) thì \(x_1^2 < x_2^2\) hay \(f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\).

Suy ra, hàm số \(y = {x^2}\) đồng biến trên \(\left( {0; + \infty } \right)\).

+ Xét khoảng \(\left( { - \infty ;0} \right)\): \(\forall {x_1},{x_2} \in \left( { - \infty ;0} \right),{x_1} < {x_2}\) thì \(x_1^2 > x_2^2\)hay \(f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\).

Suy ra, hàm số \(y = {x^2}\) nghịch biến trên \(\left( { - \infty ;0} \right)\).

LT1

Trả lời câu hỏi Luyện tập 1 trang 6 SGK Toán 12 Kết nối tri thức

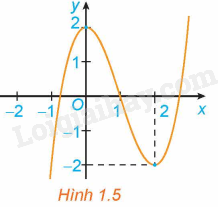
Hình 1.5 là đồ thị của hàm số \(y = {x^3} - 3{x^2} + 2\). Hãy tìm các khoảng đồng biến, khoảng nghịch biến của hàm số.

Phương pháp giải:

Sử dụng kiến thức về tính đồng biến, nghịch biến của hàm số để tìm khoảng đồng biến, nghịch biến:

+ Nếu hàm số đồng biến trên K thì đồ thị của hàm số đi lên từ trái sang phải.

+ Nếu hàm số nghịch biến trên K thì đồ thị của hàm số đi xuống từ trái sang phải.

Lời giải chi tiết:

Tập xác định của hàm số là \(\mathbb{R}\).

Trong khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {2; + \infty } \right)\) thì đồ thị hàm số \(y = {x^3} - 3{x^2} + 2\) đi lên từ trái sang phải nên hàm số \(y = {x^3} - 3{x^2} + 2\) đồng biến trên khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {2; + \infty } \right)\).

Trong khoảng \(\left( {0;2} \right)\) thì đồ thị hàm số \(y = {x^3} - 3{x^2} + 2\) đi xuống từ trái sang phải nên hàm số \(y = {x^3} - 3{x^2} + 2\) nghịch biến trên khoảng \(\left( {0;2} \right)\).

HĐ2

Trả lời câu hỏi Hoạt động 2 trang 6 SGK Toán 12 Kết nối tri thức

a) Xét dấu đạo hàm của hàm số trên các khoảng \(\left( { - \infty ; - 1} \right)\), \(\left( {1; + \infty } \right)\). Nêu nhận xét về mối quan hệ giữa tính đồng biến, nghịch biến và dấu của đạo hàm trên mỗi khoảng này.

b) Có nhận xét gì về đạo hàm y’ của hàm số y trên khoảng \(\left( { - 1;1} \right)\)?

Phương pháp giải:

Sử dụng kiến thức về tính đồng biến, nghịch biến của hàm số để tìm nhận xét:

+ Nếu hàm số đồng biến trên K thì đồ thị của hàm số đi lên từ trái sang phải.

+ Nếu hàm số nghịch biến trên K thì đồ thị của hàm số đi xuống từ trái sang phải.

Lời giải chi tiết:

a) + Xét khoảng \(\left( { - \infty ; - 1} \right)\) ta có: \(y' = \left( { - x} \right)' =  - 1 < 0\)

Trong khoảng \(\left( { - \infty ; - 1} \right)\) ta thấy hàm số y nghịch biến và đạo hàm \(y' < 0\).

+ Xét khoảng \(\left( {1; + \infty } \right)\) ta có: \(y' = x' = 1 > 0\)

Trong khoảng \(\left( {1; + \infty } \right)\) ta thấy hàm số y đồng biến và đạo hàm \(y' > 0\).

b) Trong khoảng \(\left( { - 1;1} \right)\) ta có: \(y' = \left( 1 \right)' = 0\)

Trong khoảng \(\left( { - 1;1} \right)\) ta thấy hàm số y không đổi và đạo hàm \(y' = 0\).

LT2

Trả lời câu hỏi Luyện tập 2 trang 7 SGK Toán 12 Kết nối tri thức

Tìm các khoảng đồng biến, khoảng nghịch biến của hàm số \(y =  - {x^2} + 2x + 3\).

Phương pháp giải:

Sử dụng kiến thức về định lí về tính đồng biến, nghịch biến của hàm số để tìm khoảng đồng biến, nghịch biến: Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên khoảng K.

+ Nếu \(f'\left( x \right) > 0\) với mọi \(x \in K\) thì hàm số \(f\left( x \right)\) đồng biến trên khoảng K.

+ Nếu \(f'\left( x \right) < 0\) với mọi \(x \in K\) thì hàm số \(f\left( x \right)\) nghịch biến trên khoảng K.

Lời giải chi tiết:

Tập xác định của hàm số là \(\mathbb{R}\).

Ta có: \(y' =  - 2x + 2,y' > 0\) với \(x \in \left( { - \infty ;1} \right)\); \(y < 0\) với \(x \in \left( {1; + \infty } \right)\).

Do đó, hàm số đồng biến trên khoảng \(\left( { - \infty ;1} \right)\) và nghịch biến trên khoảng \(\left( {1; + \infty } \right)\).

HĐ3

Trả lời câu hỏi Hoạt động 3 trang 7 SGK Toán 12 Kết nối tri thức

Cho hàm số \(y = f\left( x \right) = {x^3} - 3{x^2} + 2x + 1\).

a) Tính đạo hàm \(f'\left( x \right)\) và tìm các điểm x mà \(f'\left( x \right) = 0\).

b) Lập bảng biến thiên của hàm số, tức là lập bảng thể hiện dấu của đạo hàm và sự đồng biến, nghịch biến của hàm số trên các khoảng tương ứng.

c) Nếu kết luận về khoảng đồng biến, nghịch biến của hàm số.

Phương pháp giải:

Cho hàm số \(y = f\left( x \right) = {x^3} - 3{x^2} + 2x + 1\).

a) Tính đạo hàm \(f'\left( x \right)\) và tìm các điểm x mà \(f'\left( x \right) = 0\).

b) Lập bảng biến thiên của hàm số, tức là lập bảng thể hiện dấu của đạo hàm và sự đồng biến, nghịch biến của hàm số trên các khoảng tương ứng.

c) Nếu kết luận về khoảng đồng biến, nghịch biến của hàm số.

Lời giải chi tiết:

a) \(f'\left( x \right) = \left( {{x^3} - 3{x^2} + 2x + 1} \right)' = 3{x^2} - 6x + 2\)

\(f'\left( x \right) = 0 \Leftrightarrow 3{x^2} - 6x + 2 = 0 \Leftrightarrow \left[ \begin{array}{l}x = \frac{{3 - \sqrt 3 }}{3}\\x = \frac{{3 + \sqrt 3 }}{3}\end{array} \right.\)

Vậy \(x = \frac{{3 - \sqrt 3 }}{3},x = \frac{{3 + \sqrt 3 }}{3}\) thì \(f'\left( x \right) = 0\)

b) Bảng biến thiên:

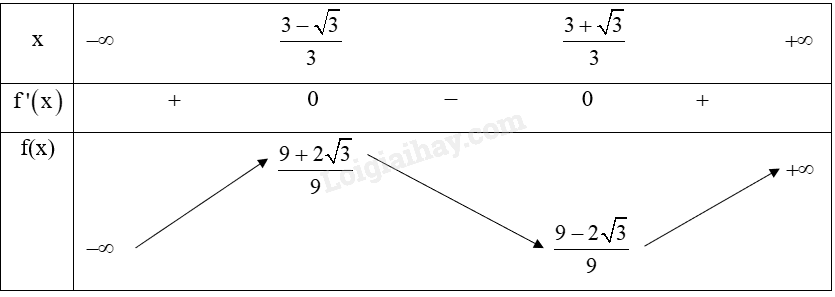
c) Hàm số \(y = f\left( x \right) = {x^3} - 3{x^2} + 2x + 1\) đồng biến trên khoảng \(\left( { - \infty ;\frac{{3 - \sqrt 3 }}{3}} \right)\) và \(\left( {\frac{{3 + \sqrt 3 }}{3}; + \infty } \right)\).

Hàm số \(y = f\left( x \right) = {x^3} - 3{x^2} + 2x + 1\) nghịch biến trên khoảng \(\left( {\frac{{3 - \sqrt 3 }}{3};\frac{{3 + \sqrt 3 }}{3}} \right)\).

LT3

Trả lời câu hỏi Luyện tập 3 trang 9 SGK Toán 12 Kết nối tri thức

Tìm các khoảng đơn điệu của các hàm số sau:

a) \(y = \frac{1}{3}{x^3} + 3{x^2} + 5x + 2\);

b) \(y = \frac{{ - {x^2} + 5x - 7}}{{x - 2}}\).

Phương pháp giải:

- Sử dụng kiến thức về các bước để xét tính đơn điệu của hàm số để tìm khoảng đơn điệu của hàm số: Các bước để xét tính đơn điệu của hàm số \(y = f\left( x \right)\):

1. Tìm tập xác định của hàm số.

2. Tính đạo hàm \(f'\left( x \right)\). Tìm các điểm \({x_i}\left( {i = 1,2,...} \right)\) mà tại đó đạo hàm bằng 0 hoặc không tồn tại.

3. Sắp xếp các điểm \({x_i}\) theo thứ tự tăng dần và lập bảng biến thiên của hàm số.

4. Nêu kết luận về khoảng đồng biến, nghịch biến của hàm số.

Lời giải chi tiết:

a) Tập xác định: \(D = \mathbb{R}\).

Ta có: \(y' = {x^2} + 6x + 5,y' = 0 \Leftrightarrow {x^2} + 6x + 5 = 0 \Leftrightarrow \left[ \begin{array}{l}x =  - 1\\x =  - 5\end{array} \right.\)

Lập bảng biến thiên của hàm số:

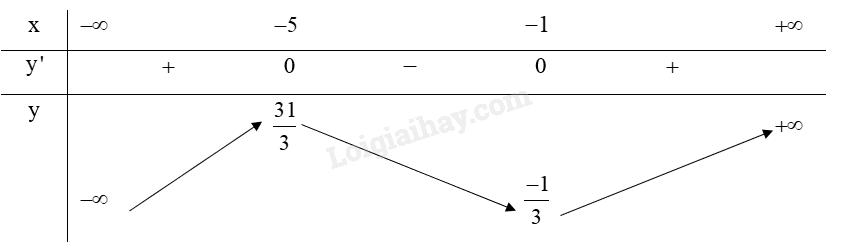
Hàm số \(y = \frac{1}{3}{x^3} + 3{x^2} + 5x + 2\) đồng biến trên khoảng \(\left( { - \infty ; - 5} \right)\) và \(\left( { - 1; + \infty } \right)\).

Hàm số \(y = \frac{1}{3}{x^3} + 3{x^2} + 5x + 2\) nghịch biến trên khoảng \(\left( { - 5; - 1} \right)\).

b) Tập xác định: \(D = \mathbb{R}\backslash \left\{ 2 \right\}\).

Ta có: \(y' = \frac{{\left( { - 2x + 5} \right)\left( {x - 2} \right) - \left( { - {x^2} + 5x - 7} \right)}}{{{{\left( {x - 2} \right)}^2}}} = \frac{{ - {x^2} + 4x - 3}}{{{{\left( {x - 2} \right)}^2}}}\)

\(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = 1\end{array} \right.\) (thỏa mãn)

Lập bảng biến thiên của hàm số:

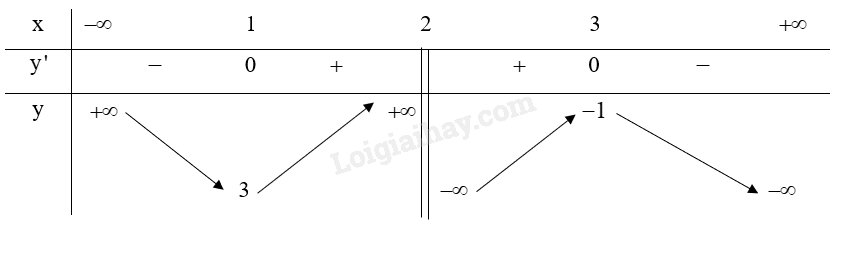Hàm số \(y = \frac{{ - {x^2} + 5x - 7}}{{x - 2}}\) đồng biến trên khoảng \(\left( {1;2} \right)\) và \(\left( {2;3} \right)\).

Hàm số \(y = \frac{{ - {x^2} + 5x - 7}}{{x - 2}}\) nghịch biến trên khoảng \(\left( { - \infty ;1} \right)\) và \(\left( {3; + \infty } \right)\).

VD1

Trả lời câu hỏi Vận dụng 1 trang 9 SGK Toán 12 Kết nối tri thức

Giải bài toán trong tình huống mở đầu bằng cách thực hiện lần lượt các yêu cầu sau:

a) Theo ý nghĩa cơ học của đạo hàm, vận tốc v(t) là đạo hàm của s(t). Hãy tìm vận tốc v(t).

b) Xét dấu của hàm v(t), từ đó suy ra câu trả lời.

Bài toán mở đầu:

Xét một chất điểm chuyển động trên một trục số nằm ngang, chiều dương từ trái sang phải (H.1.1). Giả sử vị trí s(t) (mét) của chất điểm trên trục số đã chọn tại thời điểm t (giây) được cho bởi công thức \(s\left( t \right) = {t^3} - 9{t^2} + 15t,t \ge 0\). Hỏi trong khoảng thời gian nào thì chất điểm chuyển động sang phải, trong khoảng thời gian nào thì chất điểm chuyển động sang trái?

Phương pháp giải:

a) Sử dụng kiến thức về ý nghĩa cơ học của đạo hàm để tìm hàm vận tốc: Theo ý nghĩa cơ học, vận tốc v(t) là đạo hàm của hàm số s(t).

b) Chất điểm chuyển động theo chiều dương khi \(v\left( t \right) > 0\).

Chất điểm chuyển động theo chiều âm khi \(v\left( t \right) < 0\)

Lời giải chi tiết:

a) Ta có: \(v\left( t \right) = s'\left( t \right) = \left( {{t^3} - 9{t^2} + 15t} \right)' = 3{t^2} - 18t + 15\)

b) Tập xác định: \(D = \mathbb{R}\).

Ta có: \(v\left( t \right) > 0 \Leftrightarrow 3{t^2} - 18t + 15 > 0 \Leftrightarrow \left( {t - 1} \right)\left( {t - 5} \right) > 0 \Leftrightarrow \left[ \begin{array}{l}t < 1\\t > 5\end{array} \right.\)

\(v\left( t \right) < 0 \Leftrightarrow 3{t^2} - 18t + 15 < 0 \Leftrightarrow \left( {t - 1} \right)\left( {t - 5} \right) < 0 \Leftrightarrow 1 < t < 5\)

Chất điểm chuyển động theo chiều dương (sang bên phải) khi \(v\left( t \right) > 0\), tức là \(t \in \left( { - \infty ;1} \right) \cup \left( {5; + \infty } \right)\).

Chất điểm chuyển động theo chiều âm (sang bên trái) khi \(v\left( t \right) < 0\), tức là \(1 < t < 5\).