Giải mục 2 trang 54 SGK Toán 11 tập 2 - Cùng khám phá
Ta biết hình hộp chữ nhật có 6 mặt là các hình chữ nhật. Quan sát một bể nuôi cá cảnh hình hộp chữ nhật (Hình 8.3).
Hoạt động 2
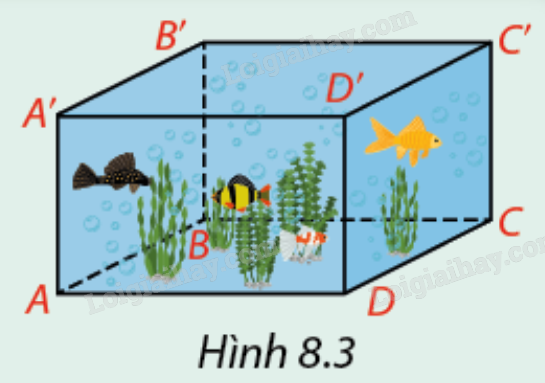
Ta biết hình hộp chữ nhật có 6 mặt là các hình chữ nhật. Quan sát một bể nuôi cá cảnh hình hộp chữ nhật (Hình 8.3). Xem mỗi cạnh của bể nuôi cá là hình ảnh thể hiện một đường thẳng. Hãy chỉ ra những đường thẳng tạo với \(AA'\) một góc \({90^o}\). Trong mỗi trường hợp, hãy cho biết vị trí tương đối của \(AA'\) và đường thẳng đã chỉ ra.
Phương pháp giải:
Để xác định góc giữa hai đường thẳng \(a,b\) ta có thể lấy điểm \(O\) thuộc đường thẳng \(a\) kẻ đường thẳng \(b'\) song song với \(b\). Khi đó \(\left( {a,b} \right) = \left( {a,b'} \right)\)
Dựa vào hình chữ nhật để tìm ra các góc vuông liên quan đến cạnh \(AA'\)
Lời giải chi tiết:
+) Ta có \(AA' \bot AB,AA' \bot AD,AA' \bot A'B',AA' \bot A'D'\) và \(AA'\) cắt các đường thẳng \(AB,AD,A'B',A'D'\)
+) Ta có \(AA' \bot CD,C'D',BC,B'C'\) và \(AA'\) chéo nhau với \(CD,C'D',BC,B'C'\)
Luyện tập 2
Cho tứ diện \(ABCD\) và điểm \(M\) thuộc cạnh \(AD\). Mặt phẳng \(\left( \alpha \right)\) đi qua \(M\), song song với \(AB\) và \(CD\). Mặt phẳng \(\left( \alpha \right)\) cắt các cạnh \(BD,CB,AC\) lần lượt tại \(N,P,Q\) (Hình 8.5). Biết \(MNPQ\) là một hình chữ nhật. Chứng minh rằng \(AB \bot CD\).

Phương pháp giải:
Để xác định góc giữa hai đường thẳng \(a,b\) ta có thể lấy điểm \(O\) thuộc đường thẳng \(a\) kẻ đường thẳng \(b'\) song song với \(b\). Khi đó \(\left( {a,b} \right) = \left( {a,b'} \right)\)
Định nghĩa: Góc giữa hai đường thẳng \(a,b\) là góc giữa hai đường thẳng \(a',b'\) cùng đi qua một điểm và lần lượt song song hoặc trùng với \(a,b\).
Chứng minh \(AB//PQ,CD//MQ\). Suy ra \(\left( {AB,CD} \right) = \left( {PQ,MQ} \right)\)
Lời giải chi tiết:
Ta có \(\left\{ \begin{array}{l}AB//\left( \alpha \right)\\\left( \alpha \right) \cap \left( {ABC} \right) = PQ\end{array} \right. \Rightarrow AB//PQ\)
Tương tự \(CD//MQ\)
Suy ra \(\left( {AB,CD} \right) = \left( {PQ,MQ} \right)\). Mà \(MNPQ\) là một hình chữ nhật nên \(\widehat {MQP} = {90^o}\)
Vậy \(\left( {AB,CD} \right) = {90^o} \Rightarrow AB \bot CD\)
Các bài khác cùng chuyên mục
- Bài 4.20 trang 114 SGK Toán 11 tập 1 - Cùng khám phá
- Lý thuyết Công thức nhân xác suất - SGK Toán 11 Cùng khám phá
- Lý thuyết Công thức cộng xác suất - SGK Toán 11 Cùng khám phá
- Lý thuyết Thể tích khối lăng trụ, khối chóp và khối chóp cụt đều - SGK Toán 11 Cùng khám phá
- Lý thuyết Khoảng cách - SGK Toán 11 Cùng khám phá
- Lý thuyết Công thức nhân xác suất - SGK Toán 11 Cùng khám phá
- Lý thuyết Công thức cộng xác suất - SGK Toán 11 Cùng khám phá
- Lý thuyết Thể tích khối lăng trụ, khối chóp và khối chóp cụt đều - SGK Toán 11 Cùng khám phá
- Lý thuyết Khoảng cách - SGK Toán 11 Cùng khám phá
- Lý thuyết Hai mặt phẳng vuông góc - SGK Toán 11 Cùng khám phá













Danh sách bình luận