Lý thuyết Hai mặt phẳng vuông góc - SGK Toán 11 Cùng khám phá
A. Lý thuyết 1. Góc nhị diện
A. Lý thuyết
1. Góc nhị diện
|
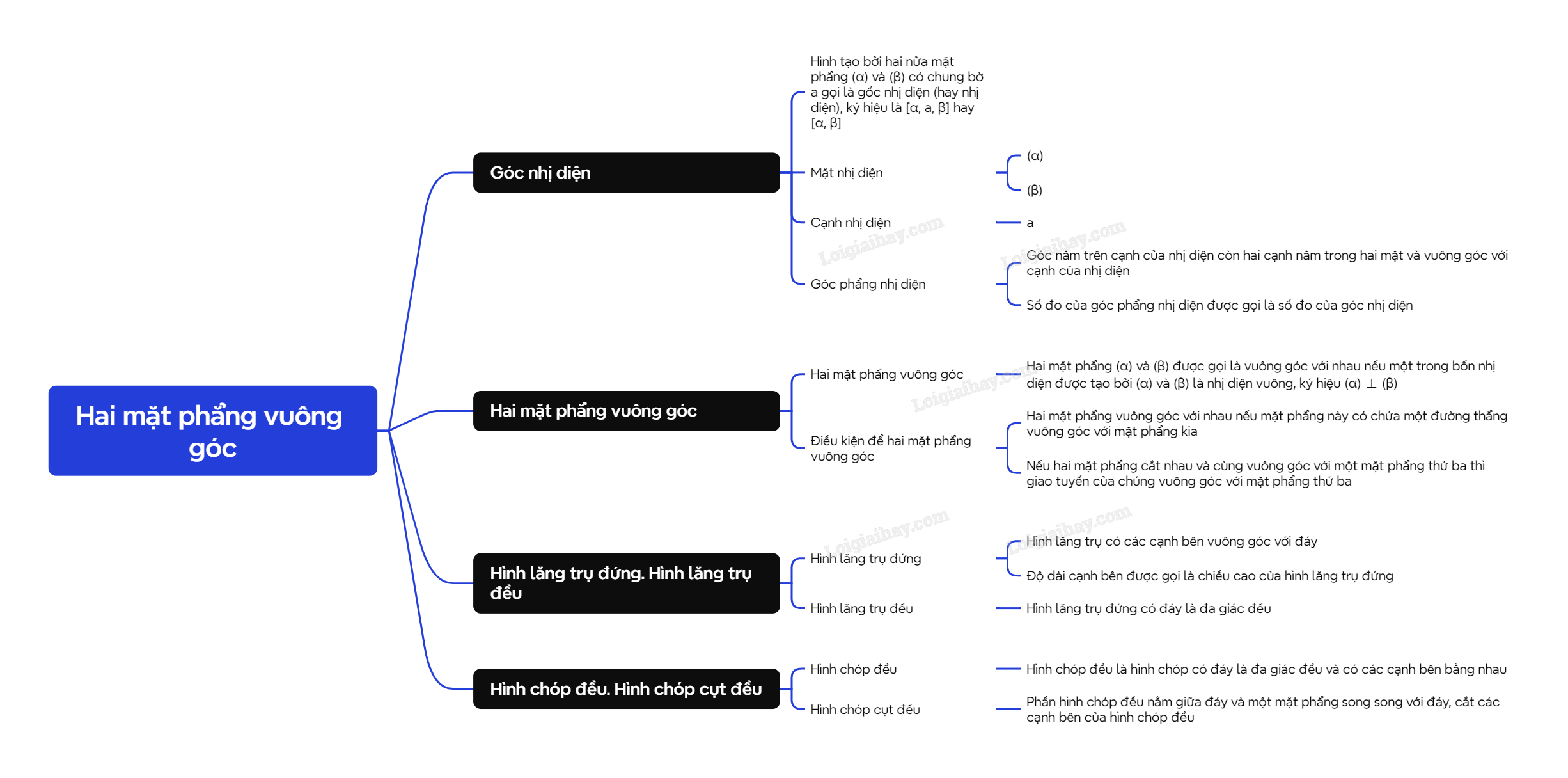
Hình tạo bởi hai nửa mặt phẳng \((\alpha )\) và \((\beta )\) có chung bờ a gọi là góc nhị diện (hay nhị diện), kí hiệu là \([\alpha ,a,\beta ]\) hay \([\alpha ,\beta ]\). Mỗi nửa mặt phẳng \((\alpha )\) và \((\beta )\) gọi là một mặt của nhị diện. Đường thẳng a gọi là cạnh của nhị diện. |
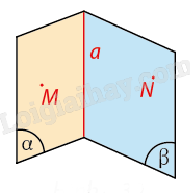
Lưu ý: Nếu trên \((\alpha )\) ta lấy điểm M, trên \((\beta )\) ta lấy điểm N (M và N đều không nằm trên a thì nhị diện đó còn được kí hiệu là [M,a,N].
|
Góc có định nghĩa nằm trên cạnh của nhị diện còn hai cạnh nằm trong hai mặt và vuông góc với cạnh của nhị diện được gọi là góc phẳng nhị diện. Số đo của góc phẳng nhị diện được gọi là số đo của góc nhị diện. |
- Nếu φ là số đo của góc nhị diện thì \({0^o} < \varphi < {180^o}\).
- Nếu số đo của góc nhị diện bằng \({90^o}\) thì hai mặt của nhị diện vuông nhau, ta có nhị diện vuông.
- Hai mặt phẳng cắt nhau tạo thành bốn nhị diện, nếu một nhị diện vuông thì ba nhị diện còn lại cũng vuông.
2. Hai mặt phẳng vuông góc
a) Hai mặt phẳng vuông góc
| Hai mặt phẳng \((\alpha )\) và \((\beta )\) được gọi là vuông góc với nhau nếu một trong bốn nhị diện được tạo bởi \((\alpha )\) và \((\beta )\) là nhị diện vuông, kí hiệu \((\alpha ) \bot (\beta )\). |
b) Điều kiện để hai mặt phẳng vuông góc
|
Hai mặt phẳng vuông góc với nhau nếu mặt phẳng này có chứa một đường thẳng vuông góc với mặt phẳng kia. Nếu hai mặt phẳng cắt nhau và cùng vuông góc với một mặt phẳng thứ ba thì giao tuyến của chúng vuông góc với mặt phẳng thứ ba. |
3. Hình lăng trụ đứng. Hình lăng trụ đều
|
Hình lăng trụ đứng là hình lăng trụ có các cạnh bên vuông góc với đáy. Độ dài cạnh bên được gọi là chiều cao của hình lăng trụ đứng. Hình lăng trụ đứng có đáy là đa giác đều được gọi là hình lăng trụ đều. |
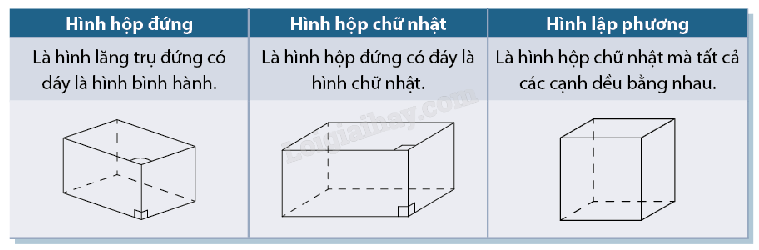
Một số tinh chất cơ bản:
- Trong hình lăng trụ đứng, các mặt bên là các hình chữ nhật và chung vuông góc với mặt đáy.
- Trong hình lăng trụ đều, các mặt bên là các hình chữ nhật có kích thước bằng nhau.
- Trong hình hộp đứng, bốn mặt bên là các hình chữ nhật.
- Trong hình hộp chữ nhật, hai mặt bên kế nhau vuông góc nhau; sáu mặt là sáu hình chữ nhật. Ngược lại, nếu sáu mặt của hình hộp là các hình chữ nhật thì hình hộp đó là hình hộp chữ nhật.
- Trong hình lập phương, sáu mặt là các hình vuông.
4. Hình chóp đều. Hình chóp cụt đều
a) Hình chóp đều
| Hình chóp đều là hình chóp có đáy là đa giác đều và có các cạnh bên bằng nhau. |
Lưu ý:
- Các mặt bên của hình chóp đều là những tam giác cân bằng nhau.
- Đường cao của hình chóp đều đi qua đỉnh và tâm của đáy.
- Độ dài đoạn thẳng nối đỉnh và tâm của đáy là chiều cao của hình chóp đều.
- Tên của hình chóp đều được gọi theo tên của đa giác đáy. Ví dụ: hình chóp tam giác đều, hình chóp tứ giác đều, hình chóp ngũ giác đều,...
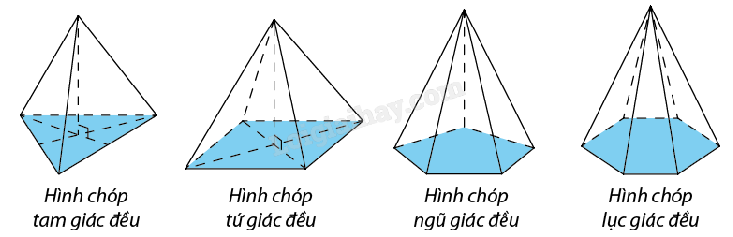
b) Hình chóp cụt đều
|
Phần hình chóp đều nằm giữa đáy và một mặt phẳng song song với đáy, cắt các cạnh bên của hình chóp đều được gọi là hình chóp cụt đều. Đáy của hình chóp đều gọi là đáy lớn của hình chóp cụt đều, còn đa giác tạo bởi mặt phẳng cắt các cạnh của hình chóp gọi là đáy nhỏ của hình chóp cụt đều đó.Các mặt còn lại gọi là mặt bên của hình chóp cụt đều. Cạnh chung của hai mặt kề nhau gọi là cạnh bên của hình chóp cụt đều. |
Lưu ý:
- Hai đáy của hình chóp cụt đều là hai đa giác đều.
- Đường thẳng nối tâm của hai đáy là đường cao của hình chóp cụt đều.
- Độ dài đoạn thẳng nối tâm của hai đáy là chiều cao của hình chóp cụt đều.
- Các mặt bên của hình chóp đều là các hình thang cân.
- Tên của hình chóp cụt đều được gợi theo hình dạng đáy của nó. Ví dụ: hình chóp cụt tứ giác đều, hình chóp cụt lục giác đều,...
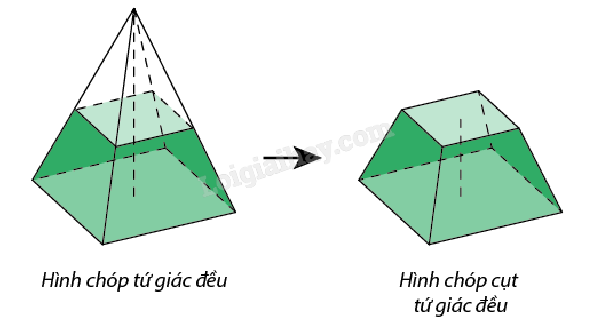
B. Bài tập
Bài 1: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt phẳng (ABC), \(SA = \frac{a}{2}\). Gọi (P) là mặt phẳng qua A và vuông góc với BC. Tính số đo của góc phẳng nhị diện [S,BC,A].
Giải:
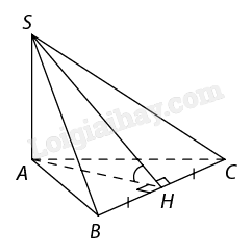
Gọi H là trung điểm BC. Ta có \(BC \bot AH\) và \(SA \bot (SAH)\).
Vậy mặt phẳng (P) chính là mặt phẳng (SAH).
Ta có giao tuyến của mặt phẳng (SAH) với mặt phẳng (SBC) và (ABC) lần lượt là SH và AH.
Vậy góc phẳng nhị diện [S,BC,A] là \(\widehat {SHA}\).
Ta có \(SA \bot AH\) (do \(SA \bot (ABC)\)) nên tam giác SAH vuông tại A.
Suy ra \(\tan \widehat {SHA} = \frac{{SA}}{{AH}} = \frac{1}{{\sqrt 3 }} \Rightarrow \widehat {SHA} = {30^o}\). Vậy số đo của góc phẳng nhị diện [S,BC,A] bằng \({30^o}\).
Bài 2: Cho tứ diện ABCD, biết ABC và DBC là hai tam giác cân có chung cạnh đáy BC. Gọi I là trung điểm của cạnh BC. Chứng minh \((DBC) \bot (ADI)\).
Giải:
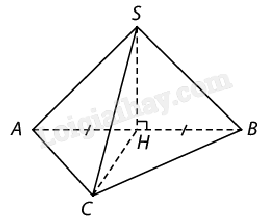
Ta có: \(BC \bot AI\) (do tam giác ABC cân tại A) và \(BC \bot DI\) (do tam giác DBC cân tại D).
Mà hai đường thẳng AI và DI cắt nhau cùng thuộc (ADI) nên \(BC \bot (ADI)\).
Mặt phẳng (BDC) chứa BC, nên \((DBC) \bot (ADI)\).
Bài 3: Cho hình chóp S.ABC có mặt phẳng (SAB) và (SAC) cùng vuông góc với đáy. Chứng minh SA vuông góc với BC.
Giải:
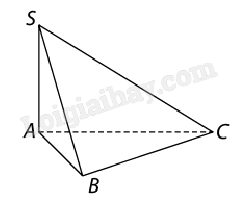
Theo giả thiết, ta có \((SAB) \bot (ABC)\) và \((SAC) \bot (ABC)\).
Mà \((SAB) \cap (SAC) = SA\).
Áp dụng định lí, suy ra \(SA \bot (ABC)\). Do đó, \(SA \bot BC\).
Bài 4: Cho hình chóp tam giác đều S.ABC. Gọi O là tâm của đường tròn ngoại tiếp tam giác ABC. Chứng minh \(SO \bot (ABC)\).
Giải:
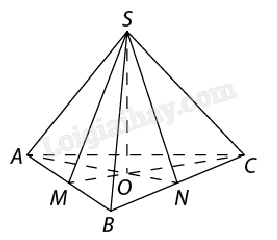
Gọi M, N lần lượt là trung điểm của AB và BC. Do O là tâm của đường tròn ngoại tiếp tam giác đều ABC nên O là giao điểm của AN và CM.
Ta có:
Tam giác SBC cân tại S, suy ra \(BC \bot SN\). Mặt khác, tam giác ABC đều, suy ra \(BC \bot AN\).
Vậy \(BC \bot (SAN)\). Mà (SAN) chứa SO nên \(BC \bot SO\) (1).
Tam giác SBA cân tại S, suy ra \(AB \bot SM\). Mặt khác, tam giác ABC đều, suy ra \(AB \bot CM\).
Từ (1) và (2) suy ra \(SA \bot (ABC)\).
Bài 5: Cho hình chóp tam giác đều S.ABC có đáy và cạnh bên đều bằng 2a, mặt phẳng (P) song song với mặt đáy (ABC) và cắt các cạnh bên SA, SB, SC lần lượt tại các trung điểm A’, B’, C’ của chúng. Tính chiều cao của hình chóp cụt đều ABC.A’B’C’.
Giải:

Gọi G và G’ lần lượt là trọng tâm các tam giác đều ABC và A’B’C’.
Ta có \(\frac{{SG'}}{{SG}} = \frac{{SA'}}{{SA}} = \frac{1}{2}\). Suy ra G’ là trung điểm của SG.
Chiều cao của hình chóp cụt đều ABC.A’B’C’ là GG’.
Tam giác ABC đều cạnh ạ, nên \(AG = \frac{{2\sqrt 3 }}{3}a\).
Ta có \(SG = \sqrt {S{A^2} - A{G^2}} = \frac{{2\sqrt 6 }}{3}a\).
Vậy chiều cao của hình chóp cụt ABC.A’B’C’ là \(G'G = \frac{{\sqrt 6 }}{3}a\).
- Giải mục 1 trang 64, 65 SGK Toán 11 tập 2 - Cùng khám phá
- Giải mục 2 trang 65, 66, 67, 68 SGK Toán 11 tập 2 - Cùng khám phá
- Giải mục 3 trang 68, 69 SGK Toán 11 tập 2 - Cùng khám phá
- Giải mục 4 trang 69, 70, 71, 72 SGK Toán 11 tập 2 - Cùng khám phá
- Bài 8.13 trang 72 SGK Toán 11 tập 2 - Cùng khám phá
>> Xem thêm
Các bài khác cùng chuyên mục
- Bài 4.20 trang 114 SGK Toán 11 tập 1 - Cùng khám phá
- Lý thuyết Công thức nhân xác suất - SGK Toán 11 Cùng khám phá
- Lý thuyết Công thức cộng xác suất - SGK Toán 11 Cùng khám phá
- Lý thuyết Thể tích khối lăng trụ, khối chóp và khối chóp cụt đều - SGK Toán 11 Cùng khám phá
- Lý thuyết Khoảng cách - SGK Toán 11 Cùng khám phá
- Lý thuyết Công thức nhân xác suất - SGK Toán 11 Cùng khám phá
- Lý thuyết Công thức cộng xác suất - SGK Toán 11 Cùng khám phá
- Lý thuyết Thể tích khối lăng trụ, khối chóp và khối chóp cụt đều - SGK Toán 11 Cùng khám phá
- Lý thuyết Khoảng cách - SGK Toán 11 Cùng khám phá
- Lý thuyết Hai mặt phẳng vuông góc - SGK Toán 11 Cùng khám phá













Danh sách bình luận