-
Toán 11 tập 1 - Cùng khám phá
-
Giải Toán 11 tập 2 - Cùng khám phá
Bài 8.13 trang 72 SGK Toán 11 tập 2 - Cùng khám phá
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, \(SA = \sqrt 3 a\), \(SA \bot \left( {ABCD} \right)\). Tính số đo của góc nhị diện \(\left[ {S,CD,A} \right]\).
Đề bài
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, \(SA = \sqrt 3 a\), \(SA \bot \left( {ABCD} \right)\). Tính số đo của góc nhị diện \(\left[ {S,CD,A} \right]\).
Phương pháp giải - Xem chi tiết
Cách tìm số đo của góc nhị diện \(\left[ {S,CD,A} \right]\):
+ Tìm giao tuyến d của (SCD) và (ACD).
+ Tìm \(a \subset \left( {SCD} \right)\) vuông góc với CD. Tìm \(b \subset \left( {ACD} \right)\) vuông góc với CD.
+ Tính \(\left( {a,b} \right)\).
Lời giải chi tiết
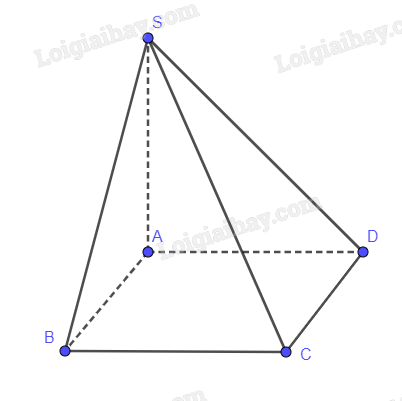
SA vuông góc với CD (Vì \(SA \bot \left( {ABCD} \right)\))
AD vuông góc với CD
Nên (SAD) vuông góc với CD
Suy ra SD vuông góc với CD
Vậy góc phẳng nhị diện \(\left[ {S,CD,A} \right]\) là góc SDA
\(\tan \widehat {SDA} = \frac{{SA}}{{AD}} = \frac{{\sqrt 3 a}}{a} = \sqrt 3 \Rightarrow \widehat {SDA} = {60^0}\)
Bình luận
Chia sẻ
- Bài 8.14 trang 72 SGK Toán 11 tập 2 - Cùng khám phá
- Bài 8.16 trang 72 SGK Toán 11 tập 2 - Cùng khám phá
- Bài 8.17 trang 72 SGK Toán 11 tập 2 - Cùng khám phá
- Bài 8.18 trang 72 SGK Toán 11 tập 2 - Cùng khám phá
- Bài 8.19 trang 72 SGK Toán 11 tập 2 - Cùng khám phá
>> Xem thêm
Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
