-
Toán 11 tập 1 - Cùng khám phá
-
Giải Toán 11 tập 2 - Cùng khám phá
Giải mục 1 trang 64, 65 SGK Toán 11 tập 2 - Cùng khám phá
Quan sát Hình 8.28, trả lời các câu hỏi:
Hoạt động 1
Quan sát Hình 8.28, trả lời các câu hỏi:
a) Bốn cánh cửa kính 1, 2, 3, 4 (Hình 8.28) chia không gian thành bao nhiêu phần?
b) Bạn An (nữ, áo vàng) và bạn Bình (nam, áo xanh) ở phần không gian nào?
Phương pháp giải:
Quan sát hình ảnh.
Lời giải chi tiết:
a) Bốn cánh cửa kính chia không gian thành 4 phần.
b) Bạn An ở phần không gian chứa cánh cửa số 1 và 4, Bình ở phần không gian chứa cánh cửa số 1 và 2.
Hoạt động 2
Cho nhị diện \(\left[ {\alpha ,a,\beta } \right]\) và điểm O thuộc a. Vẽ mặt phẳng (P) qua O và vuông góc a. Gọi giao tuyển của (P) với các nửa mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) lần lượt là các tia Ox, Oy. Hỏi số đo góc xOy thay đổi như thế nào khi điểm O thay đổi trên a?
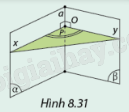
Phương pháp giải:
Quan sát hình vẽ.
Lời giải chi tiết:
Số đo góc xOy không thay đổi khi điểm O thay đổi trên A.
Luyện tập 1
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD), \(SA = \frac{{\sqrt 2 }}{2}a\). Tính số đo của các góc nhị diện \(\left[ {S,BD,A} \right]\), \(\left[ {S,BD,C} \right]\).
Phương pháp giải:
Cách tìm số đo của góc nhị diện \(\left[ {S,CD,A} \right]\):
+ Tìm giao tuyến d của (SCD) và (ACD).
+ Tìm \(a \subset \left( {SCD} \right)\) vuông góc với d. Tìm \(b \subset \left( {ACD} \right)\) vuông góc với d.
+ Tính \(\left( {a,b} \right)\).
Lời giải chi tiết:
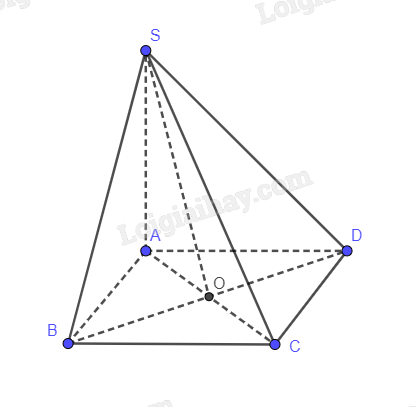
SA vuông góc với BD (Vì SA vuông góc với (ABCD))
AC vuông với BD (Vì ABCD là hình vuông)
Nên (SAC) vuông với BD
Trong (ABCD), gọi O là giao điểm của AC và BD
Suy ra SO vuông góc với BD
Mà: AO vuông góc với BD
Suy ra góc phẳng nhị diện \(\left[ {S,BD,A} \right]\) là góc SOA
ABCD là hình vuông cạnh a nên AC bằng \(\sqrt 2 a\). Suy ra AO = \(\frac{{\sqrt 2 }}{2}a\)
\(\tan \widehat {SOA} = \,\frac{{SA}}{{AO}} = \frac{{\frac{{\sqrt 2 }}{2}a}}{{\frac{{\sqrt 2 }}{2}a}} = 1 \Rightarrow \widehat {SOA} = {45^0}\)
Ta có: SO vuông góc với BD, CO vuông góc với BD nên góc phẳng nhị diện \(\left[ {S,BD,C} \right]\) là góc SOC
\(\widehat {SOC} = {180^0} - {45^0} = {135^0}\)
Bình luận
Chia sẻ
- Giải mục 2 trang 65, 66, 67, 68 SGK Toán 11 tập 2 - Cùng khám phá
- Giải mục 3 trang 68, 69 SGK Toán 11 tập 2 - Cùng khám phá
- Giải mục 4 trang 69, 70, 71, 72 SGK Toán 11 tập 2 - Cùng khám phá
- Bài 8.13 trang 72 SGK Toán 11 tập 2 - Cùng khám phá
- Bài 8.14 trang 72 SGK Toán 11 tập 2 - Cùng khám phá
>> Xem thêm
Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
