-
Toán 11 tập 1 - Cùng khám phá
-
Giải Toán 11 tập 2 - Cùng khám phá
Lý thuyết Thể tích khối lăng trụ, khối chóp và khối chóp cụt đều - SGK Toán 11 Cùng khám phá
A. Lý thuyết 1. Thể tích khối lăng trụ
A. Lý thuyết
1. Thể tích khối lăng trụ
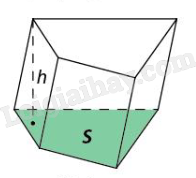
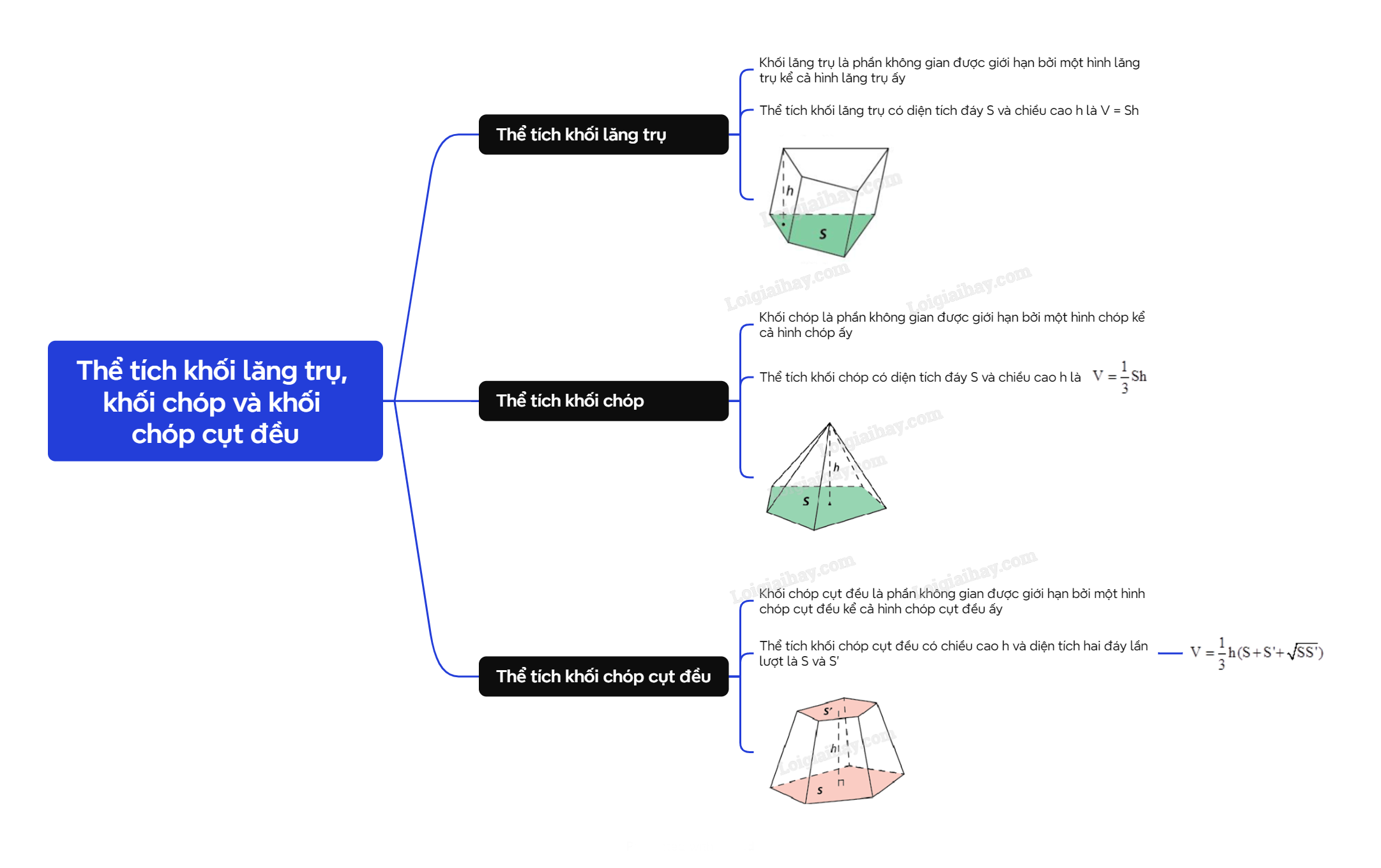
| Khối lăng trụ là phần không gian được giới hạn bởi một hình lăng trụ kể cả hình lăng trụ ấy. |
Lưu ý: Tên của khối lăng trụ được đặt theo tên của hình lăng trụ giới hạn nó.
| Thể tích khối lăng trụ có diện tích đáy S và chiều cao h là V = Sh. |
2. Thể tích khối chóp
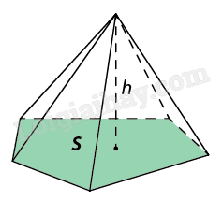
| Khối chóp là phần không gian được giới hạn bởi một hình chóp kể cả hình chóp ấy. |
Lưu ý: Tên của khối chóp được đặt theo tên của hình chóp giới hạn nó.
| Thể tích khối chóp có diện tích đáy S và chiều cao h là \(V = \frac{1}{3}Sh\). |
3. Thể tích khối chóp cụt đều
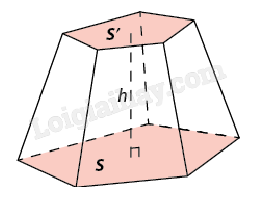
| Khối chóp cụt đều là phần không gian được giới hạn bởi một hình chóp cụt đều kể cả hình chóp cụt đều ấy. |
Lưu ý: Tên của khối chóp cụt dều được đặt theo tên của hình chóp cụt đều giới hạn nó.
|
Thể tích khối chóp cụt đều có chiều cao h và diện tích hai đáy lần lượt là S và S’: \(V = \frac{1}{3}h(S + S' + \sqrt {SS'} )\). |
B. Bài tập
Bài 1: Cho hình lăng trụ ABCD.A’B’C’D’ có cạnh bên bằng 2a, đáy là hình vuông ABCD cạnh a. Hình chiếu của A’ trên mặt phẳng (ABCD) là giao điểm O của AC và BD. Tính thể tích khối lăng trụ này.
Giải:
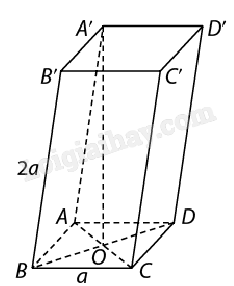
ABCD là hình vuông cạnh a nên diện tích hình vuông ABCD là \({S_{ABCD}} = {a^2}\).
Hình chiếu của A’ trên (ABCD) là O nên chiều cao hình lăng trụ là A’O.
Ta có: \(A'{O^2} = A'{A^2} - A{O^2} = 4{a^2} - {\left( {\frac{{\sqrt 2 }}{2}a} \right)^2} = \frac{{14{a^2}}}{4} \Rightarrow A'O = \frac{{\sqrt {14} }}{2}a\).
Vậy thể tích khối lăng trụ đã cho là \(V = A'O.{S_{ABCD}} = \frac{{\sqrt {14} }}{2}{a^3}\).
Bài 2: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, cạnh bên SA vuông góc với mặt phẳng đáy và SA = a. Biết rằng \(AB = \sqrt 2 a\), \(AC = \sqrt 3 a\). Tính thể tích của khối chóp này.
Giải:
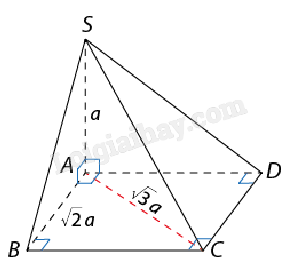
Ta có A là hình chiếu của A trên mặt đáy (ABCD) nên chiều cao của hình chóp S.ABCD là SA = a.
Vì ABCD là hình chữ nhật nên \(B{C^2} = A{C^2} - A{B^2} = {a^2} \Rightarrow BC = a\) nên diện tích ABCD là \({S_{ABCD}} = AB.BC = \sqrt 2 {a^2}\).
Vậy thể tích khối chóp S.ABCD là \({V_{S.ABCD}} = \frac{1}{3}SA.{S_{ACBD}} = \frac{{\sqrt 2 }}{3}{a^3}\).
Bài 3: Một phòng ngủ ngoài trời có hình dạng hình chóp cụt đều, cạnh đáy lớn bằng 150 cm, cạnh đáy nhỏ bằng 120 cm, chiều cao 180 cm. Tính thể tích phần không gian bên trong phòng ngủ.
Giải:
Cạnh đáy lớn bằng 150 cm nên diện tích đáy lớn là \(S = {150^2} = 22500\) \((c{m^2})\).
Cạnh đáy nhỏ bằng 120 cm nên diện tích đáy nhỏ là \(S' = {120^2} = 14400\) \((c{m^2})\).
Chiều cao chóp cụt là h = 180 cm.
Thể tích phòng ngủ là \(V = \frac{1}{3}h(S + S' + \sqrt {SS'} ) = 3294000\) \((c{m^3})\).
Bình luận
Chia sẻ
- Giải mục 1 trang 80 SGK Toán 11 tập 2 - Cùng khám phá
- Giải mục 2 trang 81, 82 SGK Toán 11 tập 2 - Cùng khám phá
- Giải mục 3 trang 83 SGK Toán 11 tập 2 - Cùng khám phá
- Bài 8.29 trang 83 SGK Toán 11 tập 2 - Cùng khám phá
- Bài 8.30 trang 83 SGK Toán 11 tập 2 - Cùng khám phá
>> Xem thêm
Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
Các bài khác cùng chuyên mục
- Lý thuyết Công thức nhân xác suất - SGK Toán 11 Cùng khám phá
- Lý thuyết Công thức cộng xác suất - SGK Toán 11 Cùng khám phá
- Lý thuyết Thể tích khối lăng trụ, khối chóp và khối chóp cụt đều - SGK Toán 11 Cùng khám phá
- Lý thuyết Khoảng cách - SGK Toán 11 Cùng khám phá
- Lý thuyết Hai mặt phẳng vuông góc - SGK Toán 11 Cùng khám phá
- Lý thuyết Công thức nhân xác suất - SGK Toán 11 Cùng khám phá
- Lý thuyết Công thức cộng xác suất - SGK Toán 11 Cùng khám phá
- Lý thuyết Thể tích khối lăng trụ, khối chóp và khối chóp cụt đều - SGK Toán 11 Cùng khám phá
- Lý thuyết Khoảng cách - SGK Toán 11 Cùng khám phá
- Lý thuyết Hai mặt phẳng vuông góc - SGK Toán 11 Cùng khám phá
