Bài 1. Tính đơn điệu và cực trị của hàm số - Toán 12 Ch..

Giải mục 2 trang 10, 11, 12 SGK Toán 12 tập 1 - Chân trời sáng tạo

Cực trị của hàm số

Lựa chọn câu để xem lời giải nhanh hơn

KP2

Trả lời câu hỏi Khám phá 2 trang 10 SGK Toán 12 Chân trời sáng tạo

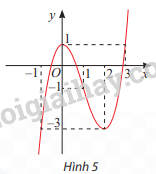
Quan sát đồ thị của hàm số \(y = f\left( x \right) = {x^3}-3{x^2} + 1{\rm{ }}\) trong Hình 5.

a) Tìm khoảng (a; b) chứa điểm x = 0 mà trên đó f(x) < f(0) với mọi \(x \ne 0\).

b) Tìm khoảng (a; b) chứa điểm x = 2 mà trên đó f(x) > f(2) với mọi \(x \ne 2\).

c) Tồn tại hay không khoảng (a; b) chứa điểm x = 1 mà trên đó f(x) > f(1) với mọi \(x \ne 1\) hoặc f(x) < f(1) với mọi \(x \ne 1\)?

Phương pháp giải:

Quan sát đồ thị.

Lời giải chi tiết:

a) Trên khoảng (-1; 2), f(x) < f(0) với mọi \(x \ne 0\).

b) Trên khoảng (0; 3), f(x) > f(2) với mọi \(x \ne 2\).

c) Không tồn tại khoảng (a; b) chứa điểm x = 1 mà trên đó f(x) > f(1) với mọi \(x \ne 1\) hoặc f(x) < f(1) với mọi \(x \ne 1\).

TH4

Trả lời câu hỏi Thực hành 4 trang 11 SGK Toán 12 Chân trời sáng tạo

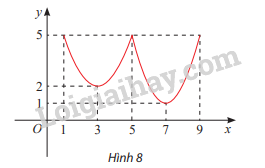
Tìm các điểm cực trị của đồ thị hàm số y = f(x) cho ở Hình 8.

Phương pháp giải:

Quan sát đồ thị.

Lời giải chi tiết:

Các điểm cực trị của đồ thị hàm số là (3;2), (5;5) và (7;1).

KP3

Trả lời câu hỏi Khám phá 3 trang 11 SGK Toán 12 Chân trời sáng tạo

Đồ thị của hàm số \(y = \left\{ \begin{array}{l}{x^2}\,\,\,khi\,\,\,x \le 1\\2 - x\,\,\,khi\,\,\,x > 1\end{array} \right.\) được cho ở Hình 9.

a) Tìm điểm cực đại và điểm cực tiểu của hàm số.

b) Tại x = 1, hàm số có đạo hàm không?

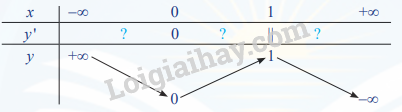
c) Thay mỗi dấu ? bằng kí hiệu (+, –) thích hợp để hoàn thành bảng biến thiên dưới đây. Nhận xét về dấu của y' khi x đi qua điểm cực đại và điểm cực tiểu.

Phương pháp giải:

Quan sát đồ thị.

Lời giải chi tiết:

a) Hàm số y = f(x) có:

x = 1 là điểm cực đại vì f (x) < f(1) với mọi \(x \in \left( {0;{\rm{ + }}\infty } \right)\backslash \left\{ 0 \right\}\).

x = 0 là điểm cực tiểu vì f(x) > f(0) với mọi \(x \in \left( { + \infty ;{\rm{ 1}}} \right)\backslash \left\{ 0 \right\}\).

b) Tại x = 1, hàm số không có đạo hàm vì đồ thị bị gấp khúc.

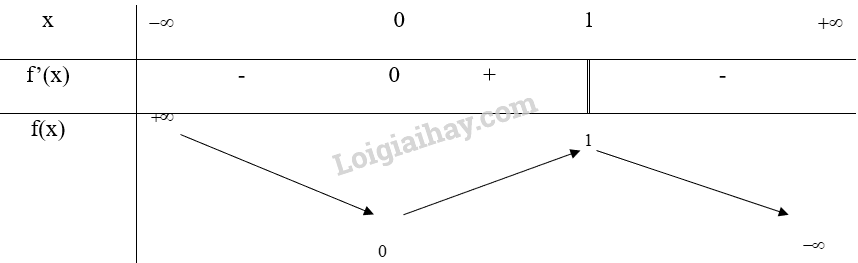
Nhận xét: Khi đi qua các điểm cực đại và cực tiểu thì y’ đổi dấu.

TH5

Trả lời câu hỏi Thực hành 5 trang 12 SGK Toán 12 Chân trời sáng tạo

Tìm cực trị của hàm số \(g\left( x \right) = \frac{{{x^2} + x + 4}}{{x + 1}}\)

Phương pháp giải:

Tìm tập xác định, g’(x) và lập bảng biến thiên

Lời giải chi tiết:

Tập xác định: \(D = \mathbb{R}\backslash \{ - 1\} \)

\(g'(x) = \frac{{{x^2} + 2x - 3}}{{{x^2} + 2x + 1}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 3\end{array} \right.\)

Bảng biến thiên:

Vậy hàm số đạt cực tiểu tại x = -3, \({y_{ct}} = f( - 3) = - 5\), đạt cực đại tại x = 1, \({y_{cd}} = f(1) = 3\)

VD2

Trả lời câu hỏi Vận dụng 2 trang 12 SGK Toán 12 Chân trời sáng tạo

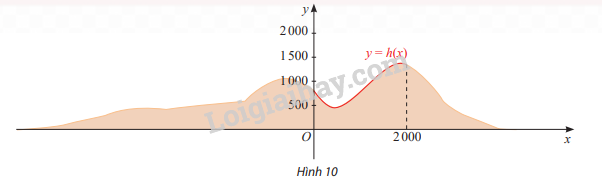
Một phần lát cắt của dãy núi có độ cao tính bằng mét được mô tả bởi hàm số \(y = h\left( x \right) = - \frac{1}{{1320000}}{x^3} + \frac{9}{{3520}}{x^2} - \frac{{81}}{{44}}x + 840\) với \(0 \le x \le 2000\).

Tìm toạ độ các đỉnh của lát cắt dãy núi trên đoạn [0; 2000].

Phương pháp giải:

Tìm h’(x) và lập bảng biến thiên.

Lời giải chi tiết:

Tập xác định: \(D = [0;2000]\).

\(h'(x) = - \frac{1}{{440000}}{x^2} + \frac{9}{{1760}}x - \frac{{81}}{{44}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1800\\x = 450\end{array} \right.\)

Bảng biến thiên:

Vậy trên đoạn [0; 2000]:

Tọa độ đỉnh cực tiểu của dãy núi là (450; 460,3125).

Tọa độ đỉnh cực đại của dãy núi là (1800; 1392,27).

👉

Giải bài nhanh với AI Hay:

Bình luận

Chia sẻ

Bình chọn:

3.7 trên 7 phiếu

Bài tiếp theo

Giải bài tập 1 trang 13 SGK Toán 12 tập 1 - Chân trời sáng tạo
Tìm các khoảng đơn điệu và cực trị của các hàm số có đồ thị cho ở Hình 11.
Giải bài tập 2 trang 13 SGK Toán 12 tập 1 - Chân trời sáng tạo
Xét tính đơn điệu và tìm điểm cực trị của các hàm số sau: a) (y = 4{x^3} + 3{x^2}--36x + 6) b) (y = frac{{{x^2} - 2x - 7}}{{x - 4}})
Giải bài tập 3 trang 13 SGK Toán 12 tập 1 - Chân trời sáng tạo
Tìm cực trị của các hàm số sau: a) (y = 2{x^3} + 3{x^2}--36x + 1) b) (y = frac{{{x^2} - 8x + 10}}{{x - 2}}) c) (y = sqrt { - {x^2} + 4} )
Giải bài tập 4 trang 13 SGK Toán 12 tập 1 - Chân trời sáng tạo
Chứng minh rằng hàm số (y = frac{{2x + 1}}{{x - 3}}) nghịch biến trên từng khoảng xác định của nó
Giải bài tập 5 trang 13 SGK Toán 12 tập 1 - Chân trời sáng tạo
Kim ngạch xuất khẩu rau quả của Việt Nam trong các năm từ 2010 đến 2017 có thể được tính xấp xỉ bằng công thức (fleft( x right) = 0,01{x^3}--0,04{x^2} + 0,25x + 0,44) (tỉ USD) với x là số năm tính từ 2010 đến 2017 ((0 le x le 7)). a) Tính đạo hàm của hàm số y = f(x). b) Chứng minh rằng kim ngạch xuất khẩu rau quả của Việt Nam tăng liên tục trong các năm từ 2010 đến 2017.
Giải bài tập 6 trang 13 SGK Toán 12 tập 1 - Chân trời sáng tạo
Xét một chất điểm chuyển động dọc theo trục (Ox). Toạ độ của chất điểm tại thời điểm (t) được xác định bởi hàm số (x(t) = {t^3} - 6{t^2} + 9t) với (t ge 0). Khi đó (x'(t)) là vận tốc của chất điểm tại thời điểm (t), kí hiệu (v(t)); (v'(t)) là gia tốc chuyển động của chất điểm tại thời điểm (t), kí hiệu (a(t)). a) Tìm các hàm (v(t))và (a(t)) b) Trong khoảng thời gian nào vận tốc của chất điểm tăng, trong khoảng thời gian nào vận tốc của chất điểm giảm?
Giải bài tập 7 trang 13 SGK Toán 12 tập 1 - Chân trời sáng tạo
Đạo hàm f '(x) của hàm số y = f(x) có đồ thị như Hình 12. Xét tính đơn điệu và tìm điểm cực trị của hàm số y = f(x).
Giải mục 1 trang 6, 7, 8 SGK Toán 12 tập 1 - Chân trời sáng tạo
Tính đơn điệu của hàm số
Giải câu hỏi mở đầu trang 6 SGK Toán 12 tập 1 - Chân trời sáng tạo
Trong 8 phút đầu kể từ khi xuất phát, độ cao h (tính bằng mét) của khinh khí cầu vào thời điểm t phút được cho bởi công thức \(h\left( t \right) = 6{t^3} - 81{t^2} + 324t\). Đồ thị của hàm số h(t) được biểu diễn trong hình bên. Trong các khoảng thời gian nào khinh khí cầu tăng dần độ cao, giảm dần độ cao? Độ cao của khinh khí cầu vào các thời điểm 3 phút và 6 phút sau khi xuất phát có gì đặc biệt?
Lý thuyết Tính đơn điệu và cực trị của hàm số Toán 12 Chân trời sáng tạo
Bài 1. Tính đơn điệu và cực trị của hàm số 1. Tính đơn điệu của hàm số