Bài 1. Đường tròn - Toán 9 Cùng khám phá

Giải mục 1 trang 98, 99, 100 SGK Toán 9 tập 1 - Cùng khám phá

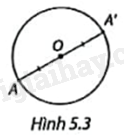
Lấy điểm A bất kì trên đường tròn và xác định điểm A’ sao cho O là trung điểm của đoạn thẳng AA’ (Hình 5.3). Điểm A’ có nằm trên đường tròn không? Vì sao?

Lựa chọn câu để xem lời giải nhanh hơn

HĐ1

Trả lời câu hỏi Hoạt động 1 trang 98 SGK Toán 9 Cùng khám phá

Lấy điểm A bất kì trên đường tròn và xác định điểm A’ sao cho O là trung điểm của đoạn thẳng AA’ (Hình 5.3). Điểm A’ có nằm trên đường tròn không? Vì sao?

Phương pháp giải:

Đường tròn tâm O, bán kính R \(\left( {R > 0} \right)\) là hình gồm tất cả các điểm trên mặt phẳng cách O một khoảng bằng R.

Lời giải chi tiết:

Vì O là trung điểm của đoạn thẳng AA’ nên \(OA = OA'\).

Do đó, điểm A’ nằm trên đường tròn tâm O, bán kính OA.

LT1

Trả lời câu hỏi Luyện tập 1 trang 99 SGK Toán 9 Cùng khám phá

Đường tròn có đường kính AB. Xác định tâm đối xứng của đường tròn.

Phương pháp giải:

Tâm của đường tròn là tâm đối xứng của đường tròn đó.

Lời giải chi tiết:

Gọi O là trung điểm của AB. Khi đó, O là tâm đường tròn đường kính AB.

Suy ra, O là tâm đối xứng của đường tròn đường kính AB.

HĐ2

Trả lời câu hỏi Hoạt động 2 trang 99 SGK Toán 9 Cùng khám phá

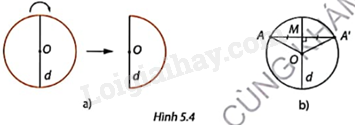
1. Cắt một hình tròn có tâm O bằng giấy và kẻ một đường kính d bất kì. Gấp đôi hình tròn theo đường kính vừa vẽ (Hình 5.4a). Hai nửa đường tròn có chồng khít lên nhau không?

2. Lấy điểm A bất kì trên đường tròn và xác định điểm A’ sao cho đường kính d là đường trung trực của đoạn thẳng AA’. So sánh OA và OA’ và cho biết điểm A’ có nằm trên đường tròn không?

Phương pháp giải:

1. Làm theo yêu cầu của đề bài, ta thấy hai nửa đường tròn chồng khít lên nhau.

2. Vì đường kính d là đường trung trực của đoạn thẳng AA’ nên \(OA = OA'\). Do đó, A’ nằm trên đường tròn tâm O.

Lời giải chi tiết:

1. Hai nửa đường tròn chồng khít lên nhau.

2. Vì đường kính d là đường trung trực của đoạn thẳng AA’ nên \(OA = OA'\).

Do đó, A’ nằm trên đường tròn tâm O.

LT2

Trả lời câu hỏi Luyện tập 2 trang 99 SGK Toán 9 Cùng khám phá

Vẽ đường tròn (O) và vẽ bốn trục đối xứng khác nhau của (O). Đường tròn (O) có bao nhiêu trục đối xứng?

Phương pháp giải:

+ Bốn trục đối xứng khác nhau của (O) là bốn đường kính của đường tròn (O).

+ Đường tròn có vô số trục đối xứng.

Lời giải chi tiết:

Bốn trục đối xứng khác nhau của (O) là bốn đường kính khác nhau của đường tròn (O) nên ta có như sau:

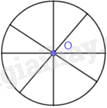
Vì đường tròn có vô số đường kính nên đường tròn có vô số trục đối xứng.

VD1

Trả lời câu hỏi Vận dụng 1 trang 100 SGK Toán 9 Cùng khám phá

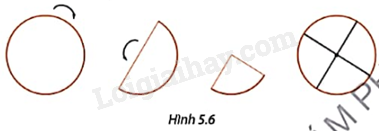
An gấp đôi tờ giấy hình tròn sao cho mép của hai nửa hình tròn trùng lên nhau, sau đó tiếp tục gấp đôi để xác định trung điểm của đường gấp đầu tiên (Hình 5.6). Bạn An khẳng định rằng giao điểm của các đường gấp sau khi mở giấy chính là tâm của hình tròn ban đầu. Em hãy giải thích vì sao?

Phương pháp giải:

Trung điểm của đường kính là tâm của đường tròn.

Lời giải chi tiết:

Khi An gấp đôi tờ giấy hình tròn sao cho mép của hai nửa hình tròn trùng lên nhau thì đường mép gấp đó chính là đường kính của hình tròn.

Khi tiếp tục gấp đôi để xác định trung điểm của đường gấp đầu tiên, tức là ta xác định trung điểm của đường kính hình tròn. Do đó, điểm đó chính là tâm của hình tròn ban đầu.

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải mục 2 trang 100, 101, 102 SGK Toán 9 tập 1 - Cùng khám phá
Trong Hình 5.7, khung cửa sổ có dạng hình tròn. Đầu mút của thanh song cửa AB nằm trên đường nào?
Giải bài tập 5.1 trang 102 SGK Toán 9 tập 1 - Cùng khám phá
Hai đường tròn có bao nhiêu trục đối xứng nếu chúng: a) Có cùng tâm? b) Không cùng tâm?
Giải bài tập 5.2 trang 102 SGK Toán 9 tập 1 - Cùng khám phá
Vận động viên X chạy trên một đường chạy có dạng đường tròn bán kính 50m xuất phát từ vị trí A. Khoảng cách lớn nhất từ vận động viên đến điểm A là bao nhiêu mét?
Giải bài tập 5.3 trang 102 SGK Toán 9 tập 1 - Cùng khám phá
Sắp xếp các đoạn thẳng AB, AC và AD trong Hình 5.13 theo thứ tự tăng dần về độ dài và giải thích.
Giải bài tập 5.4 trang 102 SGK Toán 9 tập 1 - Cùng khám phá
Cho đường tròn tâm O và AB là một dây không đi qua tâm của (O). Gọi M là trung điểm của đoạn thẳng AB. a) Chứng minh rằng OM vuông góc với AB. b) Biết bán kính của đường tròn (O) là 10cm và \(OM = 6cm\), tính độ dài dây AB.
Giải bài tập 5.5 trang 102 SGK Toán 9 tập 1 - Cùng khám phá
Trong Hình 5.14, cho hai đường tròn cùng tâm O, các điểm A, B, C, D thẳng hàng và \(OH \bot AB\left( {H \in AB} \right)\). a) Chứng minh rằng H là trung điểm của AB và CD. b) Chứng minh rằng \(AC = BD\). c) Biết bán kính đường tròn lớn là 10cm, \(CD = 16cm\) và \(AB = 8cm\). Tính bán kính đường tròn nhỏ.
Giải câu hỏi khởi động trang 98 SGK Toán 9 tập 1 - Cùng khám phá
Khi được chụp từ trên xuống dưới, mặt của một ổ bánh mì có dạng hình tròn. Bánh mì được cắt thành nhiều lát như trong Hình 5.1. Đường cắt nào là dài nhất?
Lý thuyết Đường tròn Toán 9 Cùng khám phá
1. Tính đối xứng và trục đối xứng của đường tròn Định nghĩa đường tròn Đường tròn tâm O, bán kính R (R > 0) là hình gồm tất cả các điểm trên mặt phẳng cách O một khoảng bằng R. Đường tròn tâm O, bán kính R được kí hiệu là (O;R) hoặc (O).