Giải mục 1 trang 56, 57, 58 Chuyên đề học tập Toán 10 - Chân trời sáng tạo

Chứng tỏ rằng nếu điểm \(M({x_0};{y_0})\) nằm trên parabol (P) thì điểm \(N({x_0}; - {y_0})\) cũng nằm trên parabol (P)

Tổng hợp đề thi học kì 1 lớp 10 tất cả các môn - Chân trời sáng tạo

Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa...

Lựa chọn câu để xem lời giải nhanh hơn

HĐ1

Chứng tỏ rằng nếu điểm \(M({x_0};{y_0})\) nằm trên parabol (P) thì điểm \(N({x_0}; - {y_0})\) cũng nằm trên parabol (P)

Lời giải chi tiết:

Nếu điểm \(M({x_0};{y_0})\) nằm trên parabol thì \({y_0}^2 = 2p{x_0} \Leftrightarrow {( - {y_0})^2} = 2p{x_0}\)

nên điểm \(M'({x_0}; - {y_0})\) cũng nằm trên parabol.

Thực hành 1

Tìm tọa độ tiêu điểm, tọa độ đỉnh, phương trình đường chuẩn và trục đối xứng của các parabol sau:

a) \(({P_1}):{y^2} = 2x\)

b) \(({P_2}):{y^2} = x\)

c) \(({P_3}):{y^2} = \frac{1}{5}x\)

Phương pháp giải:

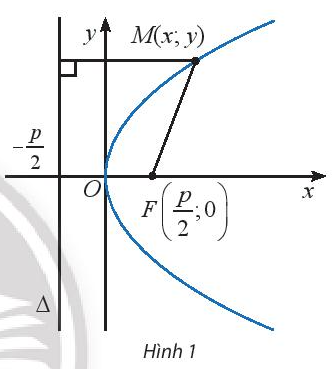
Cho parabol có PTCT \({y^2} = 2px\)

+ Tiêu điểm: \(F\left( {\frac{p}{2};0} \right)\)

+ Đỉnh O(0;0)

+ Đường chuẩn: \(\Delta :x = - \frac{p}{2}\)

+ Trục đối xứng: Ox

Lời giải chi tiết:

a) Ta có: \(2p = 2\), suy ra \(p = 1\).

Vậy \(({P_1})\) có tiêu điểm \(F\left( {\frac{1}{2};0} \right)\), đỉnh \(O(0;0)\), đường chuẩn \(\Delta :x = - \frac{1}{2}\) và nhận Ox làm trục đối xứng.

b) Ta có: \(2p = 1\), suy ra \(p = \frac{1}{2}\).

Vậy \(({P_2})\) có tiêu điểm \(F\left( {\frac{1}{4};0} \right)\), đỉnh \(O(0;0)\), đường chuẩn \(\Delta :x = - \frac{1}{4}\) và nhận Ox làm trục đối xứng.

c) Ta có: \(2p = \frac{1}{5}\), suy ra \(p = \frac{1}{{10}}\).

Vậy \(({P_2})\) có tiêu điểm \(F\left( {\frac{1}{{20}};0} \right)\), đỉnh \(O(0;0)\), đường chuẩn \(\Delta :x = - \frac{1}{{20}}\) và nhận Ox làm trục đối xứng.

Vận dụng 1

Trong mặt phẳng Oxy, cho điểm \(A(2;0)\) và đường thẳng \(d:x + 2 = 0\). Viết phương trình của đường (L) là tập hợp các tâm \(J(x;y)\) của các đường tròn (C) thay đổi nhưng luôn luôn đi qua A và tiếp xúc với d.

Lời giải chi tiết:

Ta có: (C) đi qua \(A(2;0)\) và tiếp xúc với \(d:x + 2 = 0\)

\(\begin{array}{l} \Rightarrow d(J,d) = JA\\ \Leftrightarrow \left| {x + 2} \right| = \sqrt {{{(x - 2)}^2} + {y^2}} \\ \Leftrightarrow {\left( {x + 2} \right)^2} = {(x - 2)^2} + {y^2}\\ \Leftrightarrow {x^2} + 4x + 4 = {x^2} - 4x + 4 + {y^2}\\ \Leftrightarrow {y^2} = 8x\end{array}\)

Tức là tâm \(J(x;y)\) của (C) nằm trên parabol (P) \({y^2} = 8x\)

Bình luận

Chia sẻ

Bình chọn:

4 trên 5 phiếu

Bài tiếp theo

Giải mục 2 trang 55, 56, 57, 58 Chuyên đề học tập Toán 10 - Chân trời sáng tạo
Cho điểm \(M(x;y)\) trên parabol (P) \({y^2} = 2px\) (Hình 2). Tính khoảng cách từ điểm M đến tiêu điểm \(F\) của (P).
Giải bài 1 trang 59 Chuyên đề học tập Toán 10 – Chân trời sáng tạo
Tìm tọa độ tiêu điểm và phương trình đường chuẩn của các parabol sau:
Giải bài 2 trang 59 Chuyên đề học tập Toán 10 – Chân trời sáng tạo
Tìm bán kính qua tiêu của điểm đã cho trên các parabol sau: a) Điểm ({M_1}(3; - 6)) trên (({P_1}):{y^2} = 12x)
Giải bài 3 trang 59 Chuyên đề học tập Toán 10 – Chân trời sáng tạo
Trong mặt phẳng Oxy, cho điểm (A(frac{1}{4};0)) và đường thẳng (d:x + frac{1}{4} = 0).
Giải bài 4 trang 59 Chuyên đề học tập Toán 10 – Chân trời sáng tạo
Cho parabol (P). Trên (P) lấy hai điểm M, N sao cho đoạn thẳng MN đi qua tiêu điểm F của (P).
Giải bài 5 trang 59 Chuyên đề học tập Toán 10 – Chân trời sáng tạo
Hãy so sánh bán kính qua tiêu của điểm M trên parabol (P) với bán kính của đường tròn tâm M, tiếp xúc với đường chuẩn của (P).
Giải bài 6 trang 59 Chuyên đề học tập Toán 10 – Chân trời sáng tạo
Một sao chổi A chuyển động theo quỹ đạo có dạng một parabol (P) nhận tâm Mặt Trời là tiêu điểm. Cho biết khoảng cách ngắn nhất giữa sao chổi A và tâm Mặt Trời là khoảng 112 km.
Giải bài 7 trang 59 Chuyên đề học tập Toán 10 – Chân trời sáng tạo
Mặt cắt của gương phản chiếu của một đèn pha có dạng một parabol (P) có phương trình chính tắc ({y^2} = 6x).