Toán 9 cùng khám phá | Giải toán lớp 9 cùng khám phá Bài 2. Bất phương trình bậc nhất một ẩn - Toán 9 Cùng k..

Giải mục 1 trang 37, 38 SGK Toán 9 tập 1 - Cùng khám phá


Chủ đầu tư khu chung cư Vạn Xuân muốn quy hoạch khu đất hình chữ nhật kích thước \(50m \times 75m\) giữa các tòa nhà bằng cách chia nó thành ba hình chữ nhật nhỏ A, B, C như Hình 2.3. Phần A dùng để làm sân tập luyện thể thao (có thể chơi bóng rổ, bóng chuyền), phần B dành để trồng cây xanh và phần C là nơi đặt cầu trượt, bập bênh cho trẻ em. Chủ đầu tư muốn chia khu đất sao cho diện tích hình A không nhỏ hơn diện tích hình B. Xét bản thiết kế của chủ đầu tư khu chung cư Vạn Xuân. a) Viết biể

Lựa chọn câu để xem lời giải nhanh hơn

HĐ1

Trả lời câu hỏi Hoạt động 1 trang 37 SGK Toán 9 Cùng khám phá

 

Chủ đầu tư khu chung cư Vạn Xuân muốn quy hoạch khu đất hình chữ nhật kích thước \(50m \times 75m\) giữa các tòa nhà bằng cách chia nó thành ba hình chữ nhật nhỏ A, B, C như Hình 2.3. Phần A dùng để làm sân tập luyện thể thao (có thể chơi bóng rổ, bóng chuyền), phần B dành để trồng cây xanh và phần C là nơi đặt cầu trượt, bập bênh cho trẻ em. Chủ đầu tư muốn chia khu đất sao cho diện tích hình A không nhỏ hơn diện tích hình B.

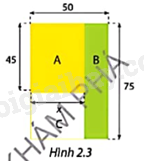
Xét bản thiết kế của chủ đầu tư khu chung cư Vạn Xuân.

a) Viết biểu thức tính diện tích hình chữ nhật A và biểu thức tính diện tích hình chữ nhật B.

b) Viết điện kiện mà số dương \(x\) cần thỏa mãn để diện tích hình A không nhỏ hơn diện tích hình B.

Phương pháp giải:

Dựa vào bất đẳng thức để giải bài toán.

Lời giải chi tiết:

a) Biểu thức tính diện tích hình chữ nhật A là: \(45x\left( {{m^2}} \right)\).

Biểu thức tính diện tích hình chữ nhật B là: \(75.\left( {50 - x} \right)\,\,\left( {{m^2}} \right)\).

b) Điều kiện mà số dương \(x\) cần thỏa mãn để diện tích hình A không nhỏ hơn diện tích hình B là: \(45x \ge 75.\left( {50 - x} \right)\).

LT1

Trả lời câu hỏi Luyện tập 1 trang 38 SGK Toán 9 Cùng khám phá

Cho một ví dụ về bất phương trình ẩn \(u\). Chỉ rõ vế trái và vế phải của bất phương trình đó.

Phương pháp giải:

Dựa vào định nghĩa bất phương trình để đưa ví dụ.

Lời giải chi tiết:

Ví dụ về bất phương trình ẩn \(u\): \(u \ge 2{u^2} - 1\).

Vế trái của bất phương trình là \(u\).

Vế phải của bất phương trình là \(2{u^2} - 1\).

HĐ2

Trả lời câu hỏi Hoạt động 2 trang 38 SGK Toán 9 Cùng khám phá

Cho bất phương trình \({x^2} < 2x + 3\).

a) Khi thay \(x = 1\) vào hai vế của bất phương trình, ta được một khẳng định đúng hay sai?

b) Khi thay \(x = 5\) vào hai vế của bất phương trình, ta được một khẳng định đúng hay sai?

Phương pháp giải:

Thay số vào hai vế của bất phương trình để giải bài toán.

Lời giải chi tiết:

a) Thay \(x = 1\) vào hai vế của bất phương trình \({x^2} < 2x + 3\), ta có: \(1 < 5\).

Đây là một khẳng định đúng.

b) Thay \(x = 5\) vào hai vế của bất phương trình \({x^2} < 2x + 3\), ta có: \(25 < 13\).

Đây là một khẳng định sai.

LT2

Trả lời câu hỏi Luyện tập 2 trang 38 SGK Toán 9 Cùng khám phá

\(x =  - 2\) là một nghiệm của bất phương trình nào trong các bất phương trình sau?

a) \(x\left( {x - 1} \right) < x + 2\);

b) \({x^2} - 2 > 0\).

Phương pháp giải:

Thay số vào bất phương trình để giải bài toán.

Lời giải chi tiết:

a) Thay \(x =  - 2\) vào hai vế của bất phương trình \(x\left( {x - 1} \right) < x + 2\), ta có: \(6 < 0\).

Đây là một khẳng định sai.

Vậy \(x =  - 2\) không phải là một nghiệm của bất phương trình.

b) Thay \(x =  - 2\) vào hai vế của bất phương trình \({x^2} - 2 > 0\), ta có: \(2 > 0\).

Đây là một khẳng định đúng.

Vậy \(x =  - 2\) là một nghiệm của bất phương trình.


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo
  • Giải mục 2 trang 39 SGK Toán 9 tập 1 - Cùng khám phá

    Trong các bất phương trình sau, bất phương trình nào có vế trái là đa thức bậc nhất một ẩn? \(3x - 8 < 0\); \(5{x^3} - 1 > 0\); \(0,5t - 4 \ge 0\); \(3 - 2y \le 0\); \(\frac{1}{{t + 1}} - \frac{1}{{2t}} > 0\); \({x^2} - 1 < 0\).

  • Giải mục 3 trang 40, 41, 42 SGK Toán 9 tập 1 - Cùng khám phá

    Cho bất phương trình \(3x + 9 > 0\). a) Để vế trái của bất phương trình chỉ còn \(3x\), ta cộng vào hai vế số nào? Viết bất phương trình thu được sau khi cộng với số đó. b) Từ bất phương trình thu được ở câu a, làm thế nào để có một bất phương trình mà hệ số của ẩn bằng 1? Đó là bất phương trình nào?

  • Giải bài tập 2.10 trang 44 SGK Toán 9 tập 1 - Cùng khám phá

    Hãy chỉ ra các bất phương trình bậc nhất một ẩn trong những bất phương trình sau: a) \(5x \le 2\). b) \({t^2} + t > 1\). c) \(\frac{1}{{x + 1}} > 0\). d) \(3u + 2 < 0\).

  • Giải bài tập 2.11 trang 44 SGK Toán 9 tập 1 - Cùng khám phá

    \(x = - 2,5\) là nghiệm của bất phương trình nào? a) \(3x - 5 < 2x - 8\). b) \(x - 1 \le 5x + 9\). c) \(5x < 12\).

  • Giải bài tập 2.12 trang 44 SGK Toán 9 tập 1 - Cùng khám phá

    Giải bất phương trình: a) \(2x - 3 > 0\). b) \(3 - 4t > 0\). c) \( - 7x + 9 \le 0\). d) \( - x - 1 \ge 0\).

>> Xem thêm

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store

Đăng ký để nhận lời giải hay và tài liệu miễn phí

Cho phép loigiaihay.com gửi các thông báo đến bạn để nhận được các lời giải hay cũng như tài liệu miễn phí.

Đồng ý Bỏ qua