A. Hoạt động thực hành - Bài 98 : Ôn tập về phân số

Câu 1

Chơi trò chơi “Đố bạn” :

a) Mỗi bạn viết một phân số rồi đọc phân số vừa viết.

b) Ghi lại các phân số nhóm em vừa viết.

c) Trong các phân số đó, phân số nào lớn nhất, phân số nào bé nhất ?

Phương pháp giải:

- Mỗi phân số có tử số và mẫu số. Tử số là số tự nhiên viết trên gạch ngang. Mẫu số là số tự nhiên khác 0 viết dưới gạch ngang.

- Để đọc phân số ta đọc tử số trước, sau đó đọc “phần” rồi đọc mẫu số.

- Để tìm phân số lớn nhất, phân số bé nhất ta so sánh các phân số.

Lời giải chi tiết:

Các em tham khảo nhé :

a)

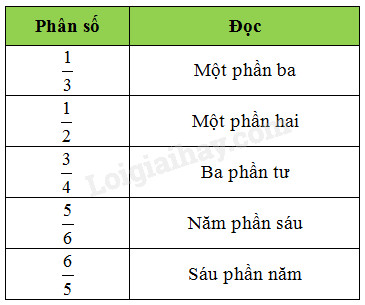
b) Các phân số nhóm em vừa viết là :

\(\dfrac{1}{3}\,\,;\,\,\,\,\,\dfrac{1}{2}\,\,;\,\,\,\,\,\dfrac{3}{4}\,\,;\,\,\,\,\,\dfrac{5}{6}\,\,;\,\,\,\,\,\dfrac{6}{5}\)

c) Trong các phân số trên, phân số nhỏ nhất là \(\dfrac{1}{3}\) và phân số lớn nhất là \(\dfrac{6}{5}\).

Câu 2

a) Viết phân số chỉ phần đã tô màu của mỗi hình dưới đây :

b) Viết hỗn số chỉ phần đã tô màu của mỗi hình dưới đây :

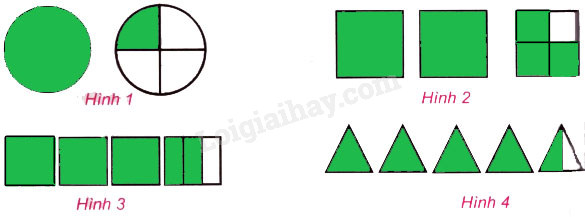
Phương pháp giải:

Quan sát hình vẽ để viết phân số hoặc hỗn số tương ứng của mỗi hình.

Lời giải chi tiết:

a) Phân số chỉ phần đã tô của các hình là :

•  Hình 1 : \(\dfrac{3}{4}\)                  •  Hình 2 : \(\dfrac{2}{5}\)

•  Hình 3 : \(\dfrac{5}{8}\)                  •  Hình 4 : \(\dfrac{3}{8}\)

b) Hỗn số chỉ phần đã tô màu của mỗi hình là :

•  Hình 1 : \(1\dfrac{1}{4}\)                •  Hình 2 : \(2\dfrac{3}{4}\)

•  Hình 3 : \(3\dfrac{2}{3}\)                •  Hình 4 : \(4\dfrac{1}{2}\) 

Câu 3

Chơi trò chơi “Ghép đôi - Tìm các phân số bằng nhau trong các phân số”:

a) Mỗi nhóm có một tấm bìa ghi phân số, mỗi bạn lấy một tấm bìa, hai bạn có tấm bìa ghi hai phân số bằng nhau ghép thành một cặp.

b) Ghi các cặp phân số bằng nhau vào vở.

Phương pháp giải:

Áp dụng tính chất cơ bản của phân số :

- Nếu nhân cả tử số và mẫu số của một phân số với cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.

- Nếu chia hết cả tử và mẫu số của một phân số cho cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.

Lời giải chi tiết:

Ta có :

\(\dfrac{4}{7} = \dfrac{{4 \times 5}}{{7 \times 5}} = \dfrac{{20}}{{35}}\)  ;     \(\dfrac{2}{5} = \dfrac{{2 \times 7}}{{5 \times 7}} = \dfrac{{14}}{{35}}\)  ;            \(\dfrac{3}{8} = \dfrac{{3 \times 6}}{{8 \times 6}} = \dfrac{{18}}{{48}}.\)

Vậy các cặp phân số bằng nhau trong các phân số trên là :

\(\dfrac{4}{7}\) và \(\dfrac{{20}}{{35}}\)  ;                     \(\dfrac{2}{5}\) và \(\dfrac{{14}}{{35}}\);                       \(\dfrac{3}{8}\) và \(\dfrac{{18}}{{48}}.\)

Câu 4

a) Viết phân số thích hợp tương ứng với vạch chỉ trung điểm của đoạn thẳng AB trên tia số : 

b) Em và bạn đổi vở, chữa bài cho nhau và thống nhất kết quả với cả nhóm.

Phương pháp giải:

Ta thấy: từ vạch \(0\) đến vạch \(1\) được chia thành \(10\) phần bằng nhau. Ta sẽ quy đồng hai phân số \( \dfrac {1}{5}\) và \( \dfrac {2}{5}\) với mẫu số chung là \(10\) rồi tìm phân số ở giữa hai phân số đó.

Lời giải chi tiết:

\( \dfrac {1}{5} = \dfrac{1 \times 2}{5\times 2 }= \dfrac {2}{10}\) ;    \( \dfrac {2}{5} = \dfrac{2 \times 2}{5\times 2 }= \dfrac {4}{10}\).

Mà: \( \dfrac {2}{10} < \dfrac{3}{10}< \dfrac {4}{10}\)

Do đó vạch ở giữa \( \dfrac {1}{5}\) và \( \dfrac {2}{5}\) ứng với phân số \( \dfrac {3}{10}.\)

Câu 5

Khoanh tròn vào chữ đặt trước câu trả lời đúng :

a) Phân số chỉ phần đã tô màu của băng giấy sau là :

A. \(\dfrac{4}{3}\)                                             B. \(\dfrac{4}{7}\)

C. \(\dfrac{3}{4}\)                                             D. \(\dfrac{3}{7}\)

b) Có 24 viên bi, trong đó có 5 viên bi xanh, 9 viên bi đỏ, 6 viên bi vàng và 4 viên bi nâu. Như vậy \(\dfrac{1}{4}\) số viên bi có màu :

A. Xanh                                        B. Đỏ

C. Vàng                                        D. Nâu

Phương pháp giải:

a) Phân số chỉ phần tô màu có tử số là số ô được tô màu và mẫu số là tổng số ô của băng giấy đó.

b) Tìm \(\dfrac{1}{4}\) số viên bi ta lấy 24 chia cho 4, từ đó biết được \(\dfrac{1}{4}\) số viên bi có màu gì.

Lời giải chi tiết:

a) Ta thấy phần tô màu chiếm 4 ô trong tất cả 7 ô.

Vậy phân số chỉ phần tô màu của băng giấy là \(\dfrac{4}{7}\).

Chọn đáp án : B. \(\dfrac{4}{7}\)

b) \(\dfrac{1}{4}\) số viên bi gồm số viên bi là :

            24 : 4 = 6 (viên bi)

Do đó, \(\dfrac{1}{4}\) số viên bi có màu vàng.

Chọn đáp án : C. Vàng.

Câu 6

Rút gọn các phân số :

\(\dfrac{5}{{10}}\,\,; \dfrac{3}{{15}}\,\,; \dfrac{{40}}{{70}}\,\,; \dfrac{{24}}{{36}}\,\,; \dfrac{{70}}{{42}}.\)

Phương pháp giải:

Khi rút gọn phân số có thể làm như sau :

- Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn \(1\).

- Chia tử số và mẫu số cho số đó.

Cứ làm như thế cho đến khi nhận được phân số tối giản.

Lời giải chi tiết:

\(\dfrac{5}{{10}} = \dfrac{{5:5}}{{10:5}} = \dfrac{1}{2}\,\,;\)    \(\dfrac{3}{{15}} = \dfrac{{3:3}}{{15:3}} = \dfrac{1}{5}\,;\)         \(\dfrac{{40}}{{70}} = \dfrac{{40:10}}{{70:10}} = \dfrac{4}{7}\,;\)

\(\dfrac{{24}}{{36}} = \dfrac{{24:12}}{{36:12}} = \dfrac{2}{3}\,;\)      \(\dfrac{{70}}{{42}} = \dfrac{{70:14}}{{42:14}} = \dfrac{5}{3}.\)

Câu 7

Câu 7 (trang 99 toán VNEN lớp 5 tập 2)

Quy đồng mẫu số các phân số :

a) \(\dfrac{5}{3}\) và \(\dfrac{1}{4}\);              b) \(\dfrac{3}{8}\) và \(\dfrac{7}{{24}}\);               c) \(\dfrac{1}{2}\,;\,\,\dfrac{2}{3}\) và \(\dfrac{3}{5}\).

Phương pháp giải:

Khi quy đồng mẫu số hai phân số có thể làm như sau:

- Lấy tử số và mẫu số của phân số thứ nhất nhân với mẫu số của phân số thứ hai.

- Lấy tử số và mẫu số của phân số thứ hai nhân với mẫu số của phân số thứ nhất.

Lời giải chi tiết:

a) Chọn \(MSC = 12.\)

Ta có :

\(\dfrac{5}{3} = \dfrac{{5 \times 4}}{{3 \times 4}} = \dfrac{{20}}{{12}}\,\, ;\)          \(\dfrac{1}{4} = \dfrac{{1 \times 3}}{{4 \times 3}} = \dfrac{3}{{12}}.\)

Vậy : Quy đồng mẫu số hai phân số \(\dfrac{5}{3}\) và \(\dfrac{1}{4}\) được hai phân số \(\dfrac{{20}}{{12}}\) và \(\dfrac{3}{{12}}.\)

b)  Chọn \(MSC = 24.\)

Ta có :

\(\dfrac{3}{8} = \dfrac{{3 \times 3}}{{8 \times 3}} = \dfrac{9}{{24}}\,\,;\)                              Giữ nguyên phân số \(\dfrac{7}{{24}}.\)

Vậy : Quy đồng mẫu số hai phân số \(\dfrac{3}{8}\) và \(\dfrac{7}{{24}}\) được hai phân số \(\dfrac{9}{{24}}\) và \(\dfrac{7}{{24}}.\)

c) Chọn \(MSC = 30.\)

Ta có :

\(\dfrac{1}{2} = \dfrac{{1 \times 15}}{{2 \times 15}} = \dfrac{{15}}{{30}}\,\,;\)      \(\dfrac{2}{3} = \dfrac{{2 \times 10}}{{3 \times 10}} = \dfrac{{20}}{{30}}\,\, ;\)          \(\dfrac{3}{5} = \dfrac{{3 \times 6}}{{5 \times 6}} = \dfrac{{18}}{{30}}.\)

Vậy : Quy đồng mẫu số các phân số \(\dfrac{1}{2}\,;\,\,\dfrac{2}{3}\) và \(\dfrac{3}{5}\)được các phân số \(\dfrac{{15}}{{30}}\, ;\,\,\dfrac{{20}}{{30}}\) và \(\dfrac{{18}}{{30}}.\)

Câu 8

Điền dấu  thích hợp (<, >, =) vào chỗ chấm:

a) \(\dfrac{{11}}{8}\,\,...\,\,\dfrac{{11}}{9}\) ;

b) \(\dfrac{4}{9}\,\,...\,\,\dfrac{3}{5}\); 

c) \(\dfrac{6}{5}\,\,...\,\,\dfrac{5}{6}\).

Phương pháp giải:

- Nếu hai phân số có cùng tử số, phân số nào có mẫu số lớn hơn thì phân số đó bé hơn và ngược lại.

- Nếu hai phân số không cùng mẫu số, ta có thể quy đồng mẫu số rồi so sánh hai phân số sau khi quy đồng.

- So sánh phân số với 1: phân số có tử số lớn hơn mẫu số thì phân số đó lớn hơn 1; phân số có tử số bé hơn mẫu số thì phân số đó bé hơn 1.

Lời giải chi tiết:

a) \(\dfrac{{11}}{8}\,\, > \,\,\dfrac{{11}}{9}\) (vì hai phân số cùng có tử số là \(11\) và \(8 < 9\)).

b) Ta có :

 \(\dfrac{4}{9} = \dfrac{{4 \times 5}}{{9 \times 5}} = \dfrac{{20}}{{45}}\,\, ;\)         \(\dfrac{3}{5} = \dfrac{{3 \times 9}}{{5 \times 9}} = \dfrac{{27}}{{45}}\,\,.\)

Vì \(\dfrac{{20}}{{45}} < \dfrac{{27}}{{45}}\) nên \(\dfrac{4}{9}\,\, < \,\,\dfrac{3}{5}\,.\)

c) Ta có : \(\dfrac{6}{5} > 1\,\,\,;\,\,\,\,\dfrac{5}{6} < 1\) hay \(\dfrac{6}{5} > 1 > \dfrac{5}{6}.\)

Vậy \(\dfrac{6}{5} > \dfrac{5}{6}.\)

Câu 9

a) Viết các phân số \(\dfrac{7}{{10}};\dfrac{{27}}{{40}};\dfrac{4}{5}\)  theo thứ tự từ bé đến lớn.

b) Viết các phân số: \(\dfrac{9}{{10}};\dfrac{9}{{11}};\dfrac{{10}}{9}\)  theo thứ tự từ lớn đến bé.

Phương pháp giải:

Áp dụng các quy tắc phân số đã học để so sánh các phân số đã cho, sau đó sắp xếp các phân số theo thứ tự từ bé đến lớn hoặc theo thứ tự từ lớn đến bé.

Lời giải chi tiết:

Ta có :

\(\dfrac{7}{{10}} = \dfrac{{7 \times 4}}{{10 \times 4}} = \dfrac{{28}}{{40}}\,\,;\)                     \(\dfrac{4}{5} = \dfrac{{4 \times 8}}{{5 \times 8}} = \dfrac{{32}}{{40}}\,\,;\)

Giữ nguyên phân số \(\dfrac{{27}}{{40}}.\)

Vì  \(\dfrac{{27}}{{40}} < \dfrac{{28}}{{40}} < \dfrac{{32}}{{40}}\) nên \(\dfrac{{27}}{{40}} < \dfrac{7}{{10}} < \dfrac{4}{5}.\)

Vậy các phân số đã cho được viết theo thứ tự từ bé đến lớn là :

\(\dfrac{{27}}{{40}}\,\, ; \dfrac{7}{{10}}\,\,\,;  \dfrac{4}{5}.\)

b)  Ta có : \(\dfrac{9}{{10}} < 1\,\,;\,\,\,\dfrac{9}{{11}} < 1\,\,\,;\,\,\,\,\dfrac{{10}}{9} > 1.\)

So sánh hai phân số \(\dfrac{9}{{10}}\) và \(\dfrac{9}{{11}}\) ta được \(\dfrac{9}{{10}} > \,\,\dfrac{9}{{11}}\)(Vì hai phân số cùng có tử số là \(9\) và \(10 < 11\)).

Do đó ta có : \(\dfrac{{10}}{9} > \dfrac{9}{{10}} > \,\,\dfrac{9}{{11}}.\)

Vậy các phân số đã cho được viết theo thứ tự từ lớn đến bé là :

\(\dfrac{{10}}{9}\,\,; \dfrac{9}{{10}}\,\,; \,\dfrac{9}{{11}}.\)

 Loigiaihay.com