A. Hoạt động thực hành - Bài 17 : Em ôn lại những gì đã học

Câu 1

Viết các phân số sau theo thứ tự từ lớn đến bé :

a) \(\dfrac{{15}}{{23}}\,;\,\,\,\,\dfrac{{13}}{{23}}\,;\,\,\,\,\dfrac{{62}}{{23}}\,;\,\,\,\,\dfrac{{12}}{{23}}\)                        b) \(\dfrac{3}{4}\,;\,\,\,\,\dfrac{2}{3}\,;\,\,\,\,\dfrac{7}{{12}}\,;\,\,\,\,\dfrac{5}{6}\)

Phương pháp giải:

- So sánh các phân số rồi sắp xếp các phân số theo thứ tự từ lớn đến bé.

*) Trong hai phân số cùng mẫu số: 

- Phân số nào có tử số bé hơn thì bé hơn.

- Phân số nào có tử số lớn hơn thì lớn hơn.

- Nếu tử số bằng nhau thì hai phân số đó bằng nhau.

*) Muốn so sánh hai phân số khác mẫu số, ta có thể quy đồng mẫu số hai phân số đó rồi so sánh các tử số của chúng.

Lời giải chi tiết:

a) Vì \(62 > \,15 > \,13 > 12\) nên \(\,\dfrac{{62}}{{23}}\,\, > \,\,\dfrac{{15}}{{23}}\,\, > \,\,\,\dfrac{{13}}{{23}}\,\, > \,\,\dfrac{{12}}{{23}}.\)

Vậy các phân số viết theo thứ tự từ lớn đến bé là \(\,\dfrac{{62}}{{23}}\,;\,\,\,\dfrac{{15}}{{23}}\,;\,\,\,\,\dfrac{{13}}{{23}}\,;\,\,\,\dfrac{{12}}{{23}}.\)

b) Chọn MSC = \(12\). Quy đồng mẫu số các phân số ta có :

\(\dfrac{3}{4} = \dfrac{{3 \times 3}}{{4 \times 3}} = \dfrac{9}{{12}}\,\,;\)                              \(\dfrac{2}{3} = \dfrac{{2 \times 4}}{{3 \times 4}} = \dfrac{8}{{12}}\,\,;\)

\(\dfrac{5}{6} = \dfrac{{5 \times 2}}{{6 \times 2}} = \dfrac{{10}}{{12}}\,\,;\)                             Giữ nguyên phân số \(\dfrac{7}{{12}}.\)

Vì \(10 > 9 > 8 > 7\) nên \(\dfrac{{10}}{{12}} > \dfrac{9}{{12}} > \dfrac{8}{{12}} > \dfrac{7}{{12}}\), hay \(\dfrac{{5}}{{6}} > \dfrac{3}{{4}} > \dfrac{2}{{3}} > \dfrac{7}{{12}}.\)

Vậy các phân số viết theo thứ tự từ lớn đến bé là \(\dfrac{{5}}{{6}}\,\,;\,\,\,\dfrac{3}{{4}}\,\,;\,\,\,\dfrac{2}{{3}}\,\,;\,\,\,\dfrac{7}{{12}}.\)

Câu 2

Tính : 

Phương pháp giải:

- Biểu thức có dấu ngoặc thì tính trong ngoặc trước, ngoài ngoặc sau.

- Biểu thức có các phép tính cộng, trừ, nhân, chia thì thực hiện phép nhân, chia trước; thực hiện phép cộng, trừ sau.

Lời giải chi tiết:

a) \(\dfrac{3}{5} - \dfrac{1}{{15}} \times \dfrac{{10}}{{13}}\)\(= \dfrac{3}{5} - \dfrac{10}{{195}} \)\(= \dfrac{{117}}{{195}} - \dfrac{{10}}{{195}} = \dfrac{{107}}{{195}}\)

b)  \(\dfrac{1}{2} + \dfrac{3}{8}:\dfrac{3}{4} = \dfrac{1}{2} - \dfrac{3}{8} \times \dfrac{4}{3} \)\(= \dfrac{1}{2} + \dfrac{{12}}{{24}} = \dfrac{1}{2} + \dfrac{1}{2} = \dfrac{2}{2} = 1\)

c) \(\left( {\dfrac{3}{5} - \dfrac{3}{{20}}} \right) \times \dfrac{4}{5} \)\(= \left( {\dfrac{{12}}{{20}} - \dfrac{3}{{20}}} \right) \times \dfrac{4}{5} = \dfrac{9}{{20}} \times \dfrac{4}{5}\)\( = \dfrac{{9 \times 4}}{{20 \times 5}} = \dfrac{{9 \times 4}}{{4 \times 5 \times 5}} = \dfrac{9}{{25}}\)

Câu 3

Giải bài toán sau :

Một mảnh vườn hình chữ nhật có chiều dài \(20m\), chiều rộng bằng \(\dfrac{3}{4}\) chiều dài.

a) Tính diện tích mảnh vườn.

b) Người ta trồng rau trên mảnh vườn đó, cứ \(15m^2\) thì thu hoạch được \(10kg\) rau. Hỏi trên cả mảnh vườn thu hoạch được bao nhiêu ki-lô-gam rau ?

Chiều rộng mảnh vườn đó là :

             \(20 ×\dfrac{3}{4}= 15\; (m)\) 

Diện tích khu đất đó là :

            \(20 × 15 = 300 \;(m^2)\)

Trên cả mảnh vườn thu hoạch được số ki-lô-gam rau là :

            \(300 : 15 × 10 = 200 \;(kg)\)

                                  Đáp số : \(200kg.\)

Phương pháp giải:

- Tính chiều rộng = chiều dài × \(\dfrac{3}{4}\).

- Tính diện tích = chiều dài × chiều rộng.

- Tìm số rau thu được : Diện tích gấp \(15m^2\) bao nhiêu lần thì số rau thu được cũng gấp lên bấy nhiêu lần.

Câu 4

Giải bài toán sau :

Để lát một cái sân hình chữ nhật có chiều dài \(24m\), chiều rộng \(18m\), người ta dùng gạch hình vuông có chiều dài \(30cm.\) Hỏi cần bao nhiêu viên gạch để lát kín nền cái sân đó? (Coi phần diện tích mạch vữa không đáng kể).

Phương pháp giải:

- Tính diện tích viên gạch = cạnh \(\times\) cạnh.

- Tính diện tích căn phòng = chiều dài \(\times \) chiều rộng.

- Tính số viên gạch cần dùng = diện tích căn phòng \(:\) diện tích viên gạch (cùng một đơn vị đo).

Lời giải chi tiết:

Diện tích một viên gạch là :

\(30 \times 30 = 900\; (cm^2)\)

Diện tích nền căn phòng là :

\(24 \times 18 = 432 (m^2)\)

\(432m^2 = 4320000cm^2\)

Số viên gạch cần dùng là :

\(4320000 : 900 = 4800\) (viên)

Đáp số: \(4800\) viên gạch.

Câu 5

 Khoanh vào chữ đặt trước câu trả lời đúng :

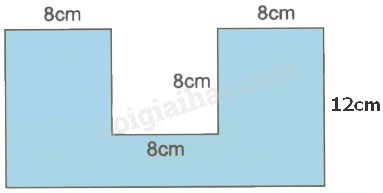
Diện tích miếng bìa có kích thước theo hình vẽ bên là :

A. \(96m^2\)                                    B. \(192m^2\) 

C. \(224m^2\)                                  D. \(288m^2\)

Phương pháp giải:

(Xem hình vẽ ở cách giải)

- Diện tích miếng bìa = diện tích hình chữ nhật MNPQ \(-\) diện tích hình vuông EGHK.

- Tính diện tích hình chữ nhật MNPQ và diện tích hình vuông EGHK theo các công thức:

       Diện tích hình chữ nhật = chiều dài \(\times\) chiều rộng.

       Diện tích hình vuông = cạnh \(\times\) cạnh.

Lời giải chi tiết:

Ta có hình vẽ như sau:

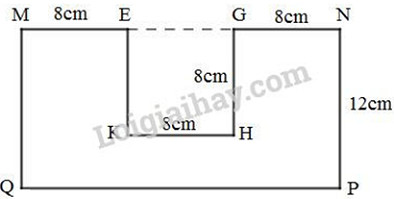
Chiều dài hình chữ nhật MNPQ là

\(8 + 8 + 8 = 24\; (cm)\)

Diện tích hình chữ nhật MNPQ là:

\(24 × 12 = 288 \;(cm^2)\)

Diện tích hình vuông EGHK là :

\(8 × 8 = 64\;(cm^2)\)

Diện tích miếng bìa là :

\(288 – 64 = 224\;(cm^2)\)

 Khoanh vào C.

Loigiaihay.com