Giải câu hỏi mở đầu trang 25 SGK Toán 12 tập 1 - Chân trời sáng tạo

Giả sử chi phí tiền xăng C (đồng) phụ thuộc tốc độ trung bình v (km/h) theo công thức:

Tổng hợp đề thi học kì 2 lớp 12 tất cả các môn - Chân trời sáng tạo

Toán - Văn - Anh - Hoá - Sinh - Sử - Địa

Đề bài

Giả sử chi phí tiền xăng C (đồng) phụ thuộc tốc độ trung bình v (km/h) theo công thức:

\(C(v) = \frac{{16000}}{v} + \frac{5}{2}v\) \(\left( {0 < v \le 120} \right)\)

Để biểu diễn trực quan sự thay đổi của C(v) theo v, người ta đã vẽ đồ thị hàm số C = C(v) như hình bên. Làm thế nào để vẽ được đồ thị hàm số này?

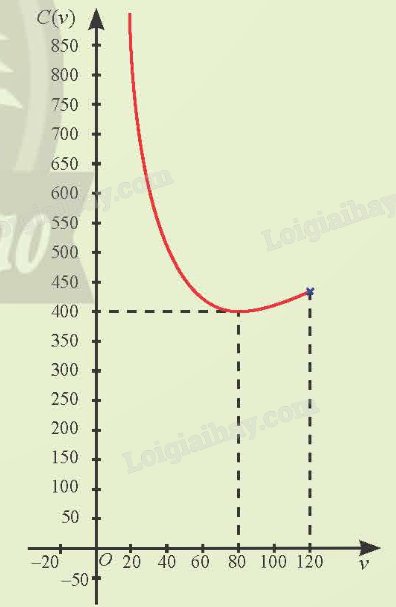
Phương pháp giải - Xem chi tiết

Thực hiện từng bước khảo sát hàm số.

Quảng cáo

Lời giải chi tiết

Khảo sát và vẽ đồ thị hàm số C = C(v):

– Tập xác định: D = (0; 120].

– Sự biến thiên:

+ Chiều biến thiên:

Đạo hàm \(C'(v) = - \frac{{16000}}{{{v^2}}} + \frac{5}{2} = \frac{{5(v - 80)(v + 80)}}{{2{v^2}}}\);

\(C'(v) = 0 \Leftrightarrow \) v = -80 (loại) hoặc v = 80.

Trên khoảng (0;80), C’(v) < 0 nên hàm số nghịch biến trên khoảng này.

Trên khoảng (80;120), C’(v) > 0 nên hàm số đồng biến trên khoảng này.

+ Cực trị: Hàm số đạt cực tiểu tại v = 80, \({C_{CT}} = C(80) = 400\).

+ Giới hạn vô cực và tiệm cận:\(\mathop {\lim }\limits_{x \to {0^ + }} C(v) = \mathop {\lim }\limits_{x \to {0^ + }} \left( {\frac{{16000}}{v} + \frac{5}{2}v} \right) = + \infty \) nên đường thẳng v = 0 là tiệm cận đứng của đồ thị hàm số.

+ Bảng biến thiên:

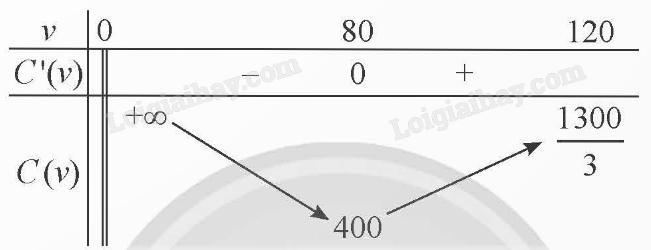
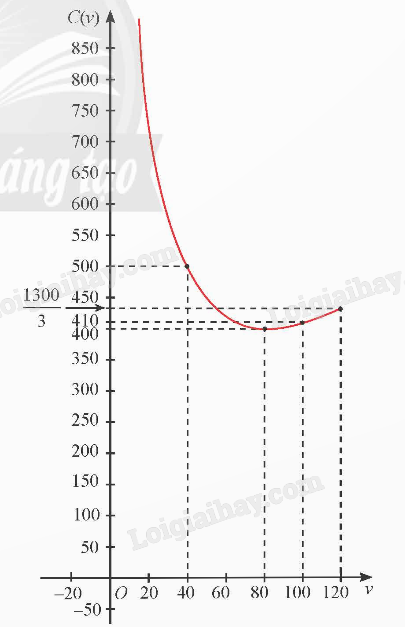
- Đồ thị: Đồ thị hàm số có điểm cực tiểu (80; 400) và đi qua các điểm (40; 500), (100; 410), \(\left( {120;\frac{{1300}}{3}} \right)\).

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải mục 1 trang 25 SGK Toán 12 tập 1 - Chân trời sáng tạo
Sơ đồ khảo sát hàm số
Giải mục 2 trang 26, 27, 28 SGK Toán 12 tập 1 - Chân trời sáng tạo
Khảo sát hàm số (y = a{x^3} + b{x^2} + cx + d(a ne 0))
Giải mục 3 trang 28,29,30 SGK Toán 12 tập 1 - Chân trời sáng tạo
Khảo sát hàm số \(y = \frac{{ax + b}}{{cx + d}}(c \ne 0,ad - bc \ne 0)\)
Giải mục 4 trang 30,31,32 SGK Toán 12 tập 1 - Chân trời sáng tạo
Khảo sát hàm số \(y = \frac{{a{x^2} + bx + c}}{{mx + n}}(a \ne 0,m \ne 0\), đa thức tử không chia hết cho đa thức mẫu)
Giải mục 5 trang 32,33,34 SGK Toán 12 tập 1 - Chân trời sáng tạo
Vận dụng đạo hàm và khảo sát hàm số để giải quyết một số vấn đề liên quan đến thực tiễn
Giải bài tập 1 trang 36 SGK Toán 12 tập 1 - Chân trời sáng tạo
Khảo sát và vẽ đồ thị của các hàm số sau: a) \(y = {x^3} + x - 2\) b) \(y = 2{x^3} + {x^2} - \frac{1}{2}x - 3\)
Giải bài tập 2 trang 36 SGK Toán 12 tập 1 - Chân trời sáng tạo
Cho hàm số \(y = {x^3} - 3{x^2} + 2\) a) Tìm điểm I thuộc đồ thị hàm số biết hoành độ của I là nghiệm của phương trình y’’ = 0. b) Chứng minh rằng I là trung điểm của đoạn thẳng nối hai điểm cực trị của đồ thị hàm số.
Giải bài tập 3 trang 36 SGK Toán 12 tập 1 - Chân trời sáng tạo
Khảo sát và vẽ đồ thị của các hàm số sau: a) \(y = 3 + \frac{1}{x}\) b) \(y = \frac{{x - 3}}{{1 - x}}\)
Giải bài tập 4 trang 36 SGK Toán 12 tập 1 - Chân trời sáng tạo
Khảo sát và vẽ đồ thị của các hàm số sau: a) (y = frac{{{x^2} - 2x + 2}}{{x - 1}}) b) (y = 2x - frac{1}{{1 - 2x}})
Giải bài tập 5 trang 36 SGK Toán 12 tập 1 - Chân trời sáng tạo
Cho hàm số: (y = frac{{ - {x^2} + 3x + 1}}{{x + 2}}) a) Khảo sát và vẽ đồ thị của hàm số đã cho. b) Tìm toạ độ trung điểm đoạn nối hai điểm cực trị của đồ thị hàm số. Có nhận xét gì về điểm này?
Giải bài tập 6 trang 36 SGK Toán 12 tập 1 - Chân trời sáng tạo
Bạn Việt muốn dùng tấm bìa hình vuông cạnh 6dm làm một chiếc hộp không nắp, có đáy là hình vuông bằng cách cắt bỏ đi 4 hình vuông nhỏ ở bốn góc của tấm bìa (Hình 11). Bạn Việt muốn tìm độ dài cạnh hình vuông cần cắt bỏ để chiếc hộp đạt thể tích lớn nhất. a) Hãy thiết lập hàm số biểu thị thể tích hộp theo x với x là độ dài cạnh hình vuông cần cắt đi. b) Khảo sát và vẽ đồ thị hàm số tìm được. Từ đó, hãy tư vấn cho bạn Việt cách giải quyết vấn đề và giải thích vì sao cần chọn giá trị này. (Làm
Lý thuyết Khảo sát và vẽ đồ thị một số hàm số cơ bản Toán 12 Chân trời sáng tạo
1. Sơ đồ khảo sát hàm số Các bước khảo sát hàm số