Giải bài tập 8 trang 87 SGK Toán 9 tập 1 - Cánh diều

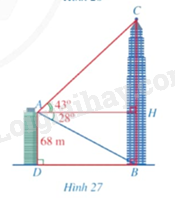
Từ vị trí (A) ở phía trên một tòa nhà có chiều cao (AD = 68m), bác Duy nhìn thấy vị trí (C) cao nhất của một tháp truyền hình, góc tạo bởi tia (AC) và tia (AH) theo phương nằm ngang là (widehat {CAH} = 43^circ ). Bác Duy cũng nhìn thấy chân tháp tại vị trí (B) mà góc tạo bởi tia (AB) và tia (AH) là (widehat {BAH} = 28^circ ), điểm (H) thuộc đoạn (BC) (Hình 27). Tính khoảng cách (BD) từ chân tháp đến chân tòa nhà và chiều cao (BC) của tháp truyền hình (làm tròn kết

Đề bài

Từ vị trí \(A\) ở phía trên một tòa nhà có chiều cao \(AD = 68m\), bác Duy nhìn thấy vị trí \(C\) cao nhất của một tháp truyền hình, góc tạo bởi tia \(AC\) và tia \(AH\) theo phương nằm ngang là \(\widehat {CAH} = 43^\circ \). Bác Duy cũng nhìn thấy chân tháp tại vị trí \(B\) mà góc tạo bởi tia \(AB\) và tia \(AH\) là \(\widehat {BAH} = 28^\circ \), điểm \(H\) thuộc đoạn \(BC\) (Hình 27). Tính khoảng cách \(BD\) từ chân tháp đến chân tòa nhà và chiều cao \(BC\) của tháp truyền hình (làm tròn kết quả đến hàng phần mười của mét).

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

Dựa vào các mối liên hệ giữa tỉ số lượng giác và các cạnh để giải bài toán.

Lời giải chi tiết

Xét tam giác \(ABD\) vuông tại \(D\) ta có:

\(BD = \frac{{AD}}{{\tan 28^\circ }} = \frac{{68}}{{\tan 28^\circ }} \approx 127,9\left( m \right)\).

Vì AHBD là hình chữ nhật nên \(BH = AD = 68m\), \(AH = BD\).

Xét tam giác \(ACH\) vuông tại \(H\) ta có:

\(CH = AH.\tan 43^\circ \approx 127,9.\tan 43^\circ \approx 119,3\left( m \right)\).

Chiều cao \(BC\) của tháp truyền hình là: \(BC = CH + BH \approx 119,3 + 68 = 187,3\left( m \right)\).

Bình luận

Chia sẻ

Bình chọn:

4 trên 5 phiếu

Bài tiếp theo

Giải bài tập 7 trang 87 SGK Toán 9 tập 1 - Cánh diều
Hình 26 minh hoạ một phần con sông có bề rộng (AB = 100m).Một chiếc thuyền đi thẳng từ vị trí (B) bên này bờ sông đến vị trí (C) bên kia bờ sông. Tính quãng đường (BC) (làm tròn kết quả đến hàng phần mười của mét), biết (widehat {ABC} = 35^circ ).
Giải bài tập 6 trang 87 SGK Toán 9 tập 1 - Cánh diều
Tính độ dài đường gấp khúc (ABCDEGH), biết các tam giác (OAB,OBC,OCD,ODE,OEG,OGH) là các tam giác vuông tại các đỉnh lần lượt là (B,C,D,E,G,H); các góc ({O_1},{O_2},{O_3},{O_4},{O_5},{O_6}) đều bằng (30^circ ) và (OA = 2cm) (Hình 25).
Giải bài tập 5 trang 87 SGK Toán 9 tập 1 - Cánh diều
Trong Hình 24, cho (widehat O = alpha ,AB = m) và (widehat {OAB} = widehat {OCA} = widehat {ODC} = 90^circ ). Chứng minh: a) (OA = m.cot alpha ); b) (AC = m.cos alpha ); c) (CD = m.{cos ^2}alpha ).
Giải bài tập 4 trang 87 SGK Toán 9 tập 1 - Cánh diều
Cho tam giác (ABC) vuông cân tại (A). Chứng minh (AB = AC = frac{{sqrt 2 }}{2}BC).
Giải bài tập 3 trang 86 SGK Toán 9 tập 1 - Cánh diều
Cho tam giác (ABC) vuông tại (A) có (widehat B = 30^circ ). Chứng minh (AC = frac{1}{2}BC).
Giải bài tập 2 trang 86 SGK Toán 9 tập 1 - Cánh diều
Cho tam giác (ABC) có đường cao (AH = 6cm,widehat B = 40^circ ,widehat C = 35^circ ). Tính độ dài các đoạn thẳng (AB,BH,AC,BC) (làm tròn kết quả đến hàng phần mười của centimét).
Giải bài tập 1 trang 86 SGK Toán 9 tập 1 - Cánh diều
Tìm (x,y) trong mỗi hình (23a,23b,23c) (làm tròn kết quả đến hàng phần mười của centimét)
Giải mục 3 trang 85, 86 SGK Toán 9 tập 1 - Cánh diều
Tìm độ dài cạnh góc vuông (AC) và số đo các góc nhọn (B,C) của tam giác vuông (ABC), biết cạnh góc vuông (AB = 5cm) và cạnh huyền (BC = 13cm).
Giải mục 2 trang 84 SGK Toán 9 tập 1 - Cánh diều
Cho tam giác (ABC) vuông tại (A) (Hình 17) a) Biểu diễn (tan B,cot C) theo (AB,AC). b) Viết công thức tính (AC) theo (AB) và (tan B). c) Viết công thức tính (AC) theo (AB) và (cot C).
Giải mục 1 trang 82, 83 SGK Toán 9 tập 1 - Cánh diều
Cho tam giác (ABC) vuông tại (A) (Hình 13). a) Biểu diễn (sin B,cos C) theo (AC,BC). b) Viết công thức tính (AC) theo (BC) và (sin B). c) Viết công thức tính (AC) theo (BC) và (cos C).
Giải câu hỏi khởi động trang 82 SGK Toán 9 tập 1 - Cánh diều
Hình 12b mô tả đường lên dốc ở Hình 12a, trong đó góc giữa (BC) và phương nằm ngang (BA) là (widehat {ABC} = 25^circ ). Cạnh góc vuông (AC) và cạnh huyền (BC) (Hình 12b) có liên hệ với nhau như thế nào?
Lý thuyết Một số hệ thức về cạnh và góc trong tam giác vuông Toán 9 Cánh diều
1. Tính cạnh góc vuông theo cạnh huyền và tỉ số lượng giác của góc nhọn Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề. Cạnh góc vuông = (cạnh huyền ) × (sin góc đối) = (cạnh huyền ) × (cosin góc kề)