 Toán 12 Cùng khám phá | Giải toán lớp 12 Cùng khám phá
Toán 12 Cùng khám phá | Giải toán lớp 12 Cùng khám phá
 Bài 1. Tính đơn điệu và cực trị của hàm số - Toán 12 Cù..
Bài 1. Tính đơn điệu và cực trị của hàm số - Toán 12 Cù..
Giải bài tập 1.6 trang 9 SGK Toán 12 tập 1 - Cùng khám phá
Cho hàm số \(y = f(x)\)có đạo hàm là \(y' = f'(x) = x{(x - 1)^2}(x + 3)\)với \(\forall x \in R\) , xác định các khoảng đồng biến nghịch biến và điểm cực trị của hàm sô \(f(x)\) đã cho
Đề bài
Cho hàm số \(y = f(x)\)có đạo hàm là \(y' = f'(x) = x{(x - 1)^2}(x + 3)\)với \(\forall x \in R\) , xác định các khoảng đồng biến nghịch biến và điểm cực trị của hàm sô \(f(x)\) đã cho
Phương pháp giải - Xem chi tiết
Bước 1: Xét \(f'(x) = 0\)
Bước 2: Lập bảng biến thiên
Bước 3: Xác định khoảng đồng biến, nghịch biến và cực trị của hàm số dựa vào bảng biến thiên
Lời giải chi tiết
Xét \(y' = f'(x) = 0\)
\( \Rightarrow x{(x - 1)^2}(x + 3) = 0\)
\( \Rightarrow \left[ \begin{array}{l}x = 0\\x = 1\\x = - 3\end{array} \right.\)
Từ đó ta có bảng biến thiên là
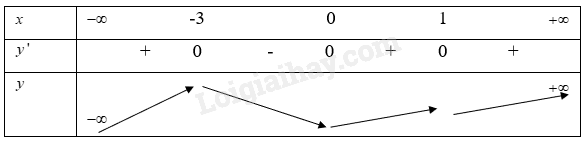
Từ bảng biến thiên ta có
Hàm số \(y = f(x)\) đồng biến trên khoảng\(( - \infty ; - 3),(0, + \infty )\)
Hàm số \(y = f(x)\) nghịch biến trên khoảng\(( - 3;0)\)
Hàm số \(y = f(x)\) đạt giá trị cực đại \(x = - 3\)
Hàm số \(y = f(x)\) đạt giá trị cực tiểu tại \(x = 0\)
- Giải bài tập 1.7 trang 9 SGK Toán 12 tập 1 - Cùng khám phá
- Giải bài tập 1.8 trang 9 SGK Toán 12 tập 1 - Cùng khám phá
- Giải bài tập 1.4 trang 9 SGK Toán 12 tập 1 - Cùng khám phá
- Giải bài tập 1.5 trang 9 SGK Toán 12 tập 1 - Cùng khám phá
- Giải bài tập 1.3 trang 9 SGK Toán 12 tập 1 - Cùng khám phá
>> Xem thêm
Các bài khác cùng chuyên mục
- Giải bài tập 6.20 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.19 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.18 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.17 trang 107 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.16 trang 107 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.20 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.19 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.18 trang 108 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.17 trang 107 SGK Toán 12 tập 2 - Cùng khám phá
- Giải bài tập 6.16 trang 107 SGK Toán 12 tập 2 - Cùng khám phá












Danh sách bình luận