Bài III.8, III.9, III.10 trang 53 SBT Vật lí 10
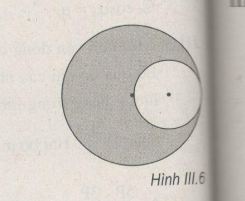
Giải bài III.8, III.9, III.10 trang 53 sách bài tập vật lý 10. Người ta khoét một lỗ tròn bán kính R/2 trong một đĩa phẳng mỏng, đồng chất, bán kính R (H.III.6). Tìm trọng tâm của phần còn lại.
III.8.
Người ta khoét một lỗ tròn bán kính R/2 trong một đĩa phẳng mỏng, đồng chất, bán kính R (H.III.6). Tìm trọng tâm của phần còn lại.
Phương pháp giải:
Áp dụng công thức
Với vật liệu đồng chất ta có:
\(\dfrac{{{P_1}}}{{{P_2}}} = \dfrac{{{S_1}}}{{{S_2}}}\)
Lời giải chi tiết:
Giả sử ta khoét thêm một lỗ tròn bán kính R/2 nữa đối xứng với lỗ tròn đã khoét lúc đầu (H.III.6G)
Gọi \(\overrightarrow {{P}} \) là trọng lượng của đĩa bán kính R khi chưa bị khoét, \(\overrightarrow {{P_1}} \) là trọng lượng của đĩa nhỏ có bán kính R/2 và \(\overrightarrow {{P_2}} \) là trọng lượng của phần đĩa còn lại sau hai lần khoét, ta có:
\(\displaystyle{{{P_1}} \over P} = {{{S_1}} \over S} = {\displaystyle{{{\pi {R^2}} \over 4}} \over {\pi {R^2}}} = {1 \over 4}\) ;
\(\displaystyle{{{P_2}} \over P} = {{S - 2{S_1}} \over S} = {{S - \displaystyle{S \over 2}} \over S} = {1 \over 2}\)
=> \(\displaystyle{{{P_1}} \over {{P_2}}} = {1 \over 2}\)
Do tính chất đối xứng, trọng tâm phần đĩa còn lại sau hai lần khoét thì trùng với tâm O của đĩa khi chưa khoét, còn trọng tâm của đĩa nhỏ mà ta giả sử khoét thêm thì ở tâm O1 của nó. Gọi G là trọng tâm của đĩa sau khi bị khoét một lỗ tròn. Ta có hệ phương trình
\(\displaystyle\left\{ \displaystyle \matrix{
{{GO} \over {G{O_1}}} = {{{P_1}} \over {{P_2}}} = {1 \over 2} \hfill \cr
GO + G{O_1} = {R \over 2} \hfill \cr} \right.\)
Giải ra ta được: \(G{O_1} = \displaystyle{R \over 3}\) và \(GO = \displaystyle{R \over 6}\)
III.9.
Lực của gió tác dụng vào cánh buồm của một chiếc thuyền buồm là F1 = 380 N hướng về phía Bắc. Nước tác dụng vào thuyền một lực F2 = 190 N hướng về phía Đông. Thuyền có khối lượng tổng cộng là 270 kg. Hỏi độ lớn và hướng của gia tốc của thuyền ?
Phương pháp giải:
- Áp dụng qui tắc tổng hợp lực: qui tắc hình bình hành
- Áp dụng định lí pytago để tính độ lớn của lực
- Áp dụng định luật II Niu ton F = m.a
Lời giải chi tiết:
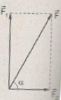
Từ hình vẽ, ta có
\(F = \sqrt {F_1^2 + F_2^2} = \sqrt {{{380}^2} + {{190}^2}}\\ = > F \approx 425N\)
\(\tan \alpha = \displaystyle{{{F_1}} \over {{F_2}}} = 2 = > \alpha = 63,{5^0}\)
\(a = \displaystyle{F \over m} = {{425} \over {270}} = 1,57(m/{s^2})\) , theo hướng Đông – Bắc.
III.10.
Một đầu tàu có khối lượng M = 50 tấn được nối với một toa xe có khối lượng m = 20 tấn. Đoàn tàu bắt đầu rời ga với gia tốc a = 0,2 m/s2. Bỏ qua ma sát lăn giữa bánh xe và mặt đường ray và khối lượng của các bánh xe. Lấy g = 10 m/s2.
a) Tính lực phát động của đầu tàu.
b) Tính lực căng ở chỗ nối.
c) Lực nào là lực kéo của đầu tàu ?
Phương pháp giải:
Áp dụng định luật II Niu ton F = m.a
Lời giải chi tiết:
a. Chọn trục Ox theo chiều chuyển động.
Lực phát động là lực ma sát nghỉ từ phía mặt đường tác dụng lên các bánh xe phát động của đầu tàu. Lực này hướng về phía trước, gây ra gia tốc cho cả đoàn tàu.
Fpd = (M + m)a = (50000 + 20000).0,2 = 14000 N.
b. Xét riêng toa xe:
T2 = ma = 20000.0,2 = 4000 N.
c. Đầu tàu kéo toa xe bằng một lực, gọi là lực kéo của đầu tàu (ở đây là lực căng T2)
Fk = 4000 N.
Loigiaihay.com













Danh sách bình luận