Giải bài 9.5 trang 51 sách bài tập toán 9 - Kết nối tri thức tập 2

Cho hai điểm B, C nằm trên đường tròn (O) và cho điểm A nằm trên cung lớn $oversetfrown{BC}$. Biết rằng (widehat {OBA} = {30^o},widehat {OCA} = {40^o}). Tính số đo các góc của tam giác ABC.

Đề bài

Cho hai điểm B, C nằm trên đường tròn (O) và cho điểm A nằm trên cung lớn $\overset\frown{BC}$. Biết rằng $\widehat {OBA} = {30^o},\widehat {OCA} = {40^o}$. Tính số đo các góc của tam giác ABC.

Phương pháp giải - Xem chi tiết

Trong một đường tròn, các góc nội tiếp chắn cung nhỏ thì có số đo bằng nửa số đo góc ở tâm chắn cùng một cung.

Lời giải chi tiết

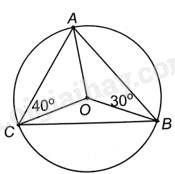
Tam giác OAB cân tại O (do $OA = OB$) nên $\widehat {OAB} = \widehat {OBA} = {30^o}$.

Lại có: $\widehat {OAB} + \widehat {OBA} + \widehat {AOB} = {180^o}$ nên $\widehat {AOB} = {180^o} - \widehat {OAB} - \widehat {OBA} = {120^o}$.

Tam giác OAC cân tại O (do $OA = OC$) nên $\widehat {OAC} = \widehat {OCA} = {40^o}$.

Lại có: $\widehat {OAC} + \widehat {OCA} + \widehat {AOC} = {180^o}$ nên $\widehat {AOC} = {180^o} - \widehat {OAC} - \widehat {OCA} = {100^o}$.

Xét đường tròn (O):

+ Góc nội tiếp ABC và góc ở tâm AOC cùng chắn cung nhỏ AC nên $\widehat {ABC} = \frac{1}{2}\widehat {AOC} = {50^o}$.

+ Góc nội tiếp ACB và góc ở tâm AOB cùng chắn cung nhỏ AB nên $\widehat {ACB} = \frac{1}{2}\widehat {AOB} = {60^o}$.

Tam giác ABC có: $\widehat {CAB} + \widehat {ACB} + \widehat {CBA} = {180^o}$ nên $\widehat {CAB} = {180^o} - \widehat {ABC} - \widehat {ACB} = {70^o}$.

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 9.6 trang 51 sách bài tập toán 9 - Kết nối tri thức tập 2
Cho đường tròn (O) có đường kính AB và điểm C thuộc đường tròn sao cho C khác A, B. Lấy E là điểm đối xứng của A qua C. Chứng minh rằng (BE = BA).
Giải bài 9.7 trang 51 sách bài tập toán 9 - Kết nối tri thức tập 2
Cho tam giác nhọn ABC cân tại A. Đường tròn đường kính AB cắt các cạnh AC, BC của tam giác ABC tại X và Y (X khác A, Y khác B). a) Chứng minh rằng tam giác CXY cân tại Y. b) Cho BX cắt AY tại K. Chứng minh rằng CK vuông góc với AB.
Giải bài 9.4 trang 51 sách bài tập toán 9 - Kết nối tri thức tập 2
Cho đường tròn (O) và hai dây cung AB, CD cắt nhau tại X. Tính số đo các góc của tam giác AXC, biết rằng (widehat {XBD} = {60^o},widehat {XDB} = {70^o}).
Giải bài 9.3 trang 50 sách bài tập toán 9 - Kết nối tri thức tập 2
Cho AB và CD là hai đường kính của đường tròn (O). Biết rằng (widehat {AOC} = {80^o}), tính số đo của các góc ABC, ADC và ABD.
Giải bài 9.2 trang 50 sách bài tập toán 9 - Kết nối tri thức tập 2
Cho điểm A nằm trên cung lớn BC của đường tròn (O) và kí hiệu $oversetfrown{BC}$ là cung nhỏ BC. Vẽ bảng sau vào vở và viết số đo còn lại của các góc hoặc cung tương ứng vào ô trống trong mỗi trường hợp:
Giải bài 9.1 trang 50 sách bài tập toán 9 - Kết nối tri thức tập 2
Hình nào dưới đây vẽ một góc nội tiếp của đường tròn?