Giải bài 7 trang 60 sách bài tập toán 12 - Chân trời sáng tạo

Một khu vực đã được thiết lập một hệ toạ độ \(Oxyz\) (đơn vị trên các trục là mét). Một flycam đang phát sóng wifi bao phủ một vùng không gian bên trong mặt cầu \(\left( S \right):{\left( {x - 20} \right)^2} + {\left( {y - 30} \right)^2} + {\left( {z - 10} \right)^2} = 400\). Một người đang sử dụng máy tính tại điểm \(M\) nằm trên điểm giao của mặt cầu \(\left( S \right)\) và mặt đất \(\left( P \right):z = 0\). a) Xác định toạ độ tâm \(I\) và bán kính của mặt cầu \(\left( S \right)\). Tính kho

Tổng hợp đề thi giữa kì 1 lớp 12 tất cả các môn - Chân trời sáng tạo

Toán - Văn - Anh - Lí - Hóa - Sinh

Đề bài

Một khu vực đã được thiết lập một hệ toạ độ \(Oxyz\) (đơn vị trên các trục là mét). Một flycam đang phát sóng wifi bao phủ một vùng không gian bên trong mặt cầu \(\left( S \right):{\left( {x - 20} \right)^2} + {\left( {y - 30} \right)^2} + {\left( {z - 10} \right)^2} = 400\). Một người đang sử dụng máy tính tại điểm \(M\) nằm trên điểm giao của mặt cầu \(\left( S \right)\) và mặt đất \(\left( P \right):z = 0\).

a) Xác định toạ độ tâm \(I\) và bán kính của mặt cầu \(\left( S \right)\). Tính khoảng cách \(IJ\) của đoạn vuông góc từ \(I\) đến \(\left( P \right)\).

b) Tính độ dài đoạn thẳng \(JM\). Làm tròn kết quả đến hàng phần trăm của mét.

Phương pháp giải - Xem chi tiết

‒ Mặt cầu \(\left( S \right):{\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} = {R^2}\) có tâm \(I\left( {a;b;c} \right)\) bán kính \(R\).

‒ Khoảng cách \(IJ\) của đoạn vuông góc từ \(I\) đến \(\left( P \right)\) chính là khoảng cách từ \(I\) đến \(\left( P \right)\).

‒ Khoảng cách từ điểm \({M_0}\left( {{x_0};{y_0};{z_0}} \right)\) đến mặt phẳng \(\left( P \right):Ax + By + C{\rm{z}} + D = 0\):

\(d\left( {{M_0};\left( P \right)} \right) = \frac{{\left| {A{x_0} + B{y_0} + C{{\rm{z}}_0} + D} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\).

Lời giải chi tiết

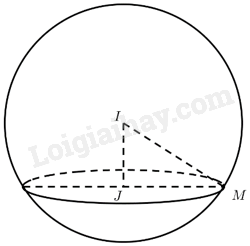
a) Mặt cầu \(\left( S \right):{\left( {x - 20} \right)^2} + {\left( {y - 30} \right)^2} + {\left( {z - 10} \right)^2} = 400\) có tâm \(I\left( {20;30;10} \right)\) bán kính \(R = \sqrt {400} = 20\).

\(IJ = d\left( {I;\left( P \right)} \right) = \frac{{\left| {10} \right|}}{{\sqrt {{0^2} + {0^2} + {1^2}} }} = 10\left( m \right)\).

b) Ta có \(M \in \left( S \right)\) nên \(IM = R = 20\).

Tam giác \(IJM\) vuông tại \(J\) nên ta có:

\(JM = \sqrt {I{M^2} - I{J^2}} = \sqrt {{{20}^2} - {{10}^2}} = 10\sqrt 3 \approx 17,32\left( m \right)\).

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 6 trang 60 sách bài tập toán 12 - Chân trời sáng tạo
Trong không gian \(Oxyz\) (đơn vị trên các trục toạ độ là mét), một ngọn hải đăng có bóng đèn đặt tại điểm \(I\left( {20;40;60} \right)\). a) Cho biết bán kính phủ sáng của đèn trên hải đăng là 3 km, viết phương trình mặt cầu biểu diễn ranh giới của vùng phủ sáng của hải đăng trong không gian. b) Một người đi biển đang ở vị trí \(M\left( {420;340;0} \right)\). Người đó có thể nhìn thấy được ánh sáng của hải đăng hay không? Giải thích.
Giải bài 5 trang 60 sách bài tập toán 12 - Chân trời sáng tạo
Người ta muốn thiết kế một quả địa cầu trong không gian \(Oxyz\) bằng phần mềm 3D. Biết phương trình mặt cầu là \(\left( S \right):{\left( {x - 24} \right)^2} + {\left( {y - 24} \right)^2} + {\left( {z - 24} \right)^2} = 100\) (đơn vị cm) và phương trình đường thẳng trục xoay là \({\rm{d}}:\frac{{x - 24}}{1} = \frac{{y - 24}}{1} = \frac{{z - 24}}{{3,25}}\). a) Tìm toạ độ giao điểm của \(d\) và \(\left( S \right)\). b) Tính số đo góc giữa \(d\) và trục \(Oz\). Làm tròn kết quả đến hàng
Giải bài 4 trang 60 sách bài tập toán 12 - Chân trời sáng tạo
Trong các phương trình sau, phương trình nào là phương trình mặt cầu? Xác định tâm và bán kính mặt của cầu đó. a) (4{x^2} + {y^2} + {z^2} - 2x - 14y - 7z + 4 = 0); b) ({x^2} + {y^2} + {z^2} + 6x - 4y - 4z - 19 = 0); c) ({x^2} + {y^2} + {z^2} - 4x - 4y - 6z + 40 = 0).
Giải bài 3 trang 59 sách bài tập toán 12 - Chân trời sáng tạo
Xác định tâm và bán kính của mặt cầu có phương trình sau: a) (left( S right):{left( {x - 7} right)^2} + {left( {y - 3} right)^2} + {left( {z + 4} right)^2} = 49); b) (left( {S'} right):{x^2} + {left( {y + 1} right)^2} + {left( {z - 2} right)^2} = 11); c) (left( S'' right):{{x}^{2}}+{{y}^{2}}+{{z}^{2}}=25)
Giải bài 2 trang 59 sách bài tập toán 12 - Chân trời sáng tạo
Viết phương trình mặt cầu \(\left( S \right)\) trong mỗi trường hợp sau: a) \(\left( S \right)\) có tâm \(I\left( {--5;7;6} \right)\) và bán kính \(R = 9\). b) \(\left( S \right)\) có tâm \(I\left( {0; - 3;0} \right)\) và đi qua điểm \(M\left( {4;0; - 2} \right)\). c) \(\left( S \right)\) có đường kính \(EF\) với \(E\left( {1;5;9} \right),F\left( {11;3;1} \right)\).
Giải bài 1 trang 59 sách bài tập toán 12 - Chân trời sáng tạo
Cho mặt cầu (left( S right)) có tâm (Ileft( {2; - 1;4} right)) và bán kính (R = 5). Các điểm (Aleft( {3;1;5} right),Bleft( { - 1;11;14} right),)(Cleft( {6;2;4} right)) nằm trong, nằm trên hay nằm ngoài mặt cầu (left( S right))?