Giải bài 7 trang 48, 49 vở thực hành Toán 7 tập 2

Cho hai đa thức (A = {x^5} + 3{x^4} - 7{x^2} + x - 2) cho (B = {x^3} + 3{x^2} - 1). a) Bằng cách đặt tính chia, hãy tìm thương và dư trong phép chia A cho B. b) Em có cách nào không cần thực hiện phép chia mà vẫn tìm được đa thức dư hay không?

Đề bài

Cho hai đa thức $A = {x^5} + 3{x^4} - 7{x^2} + x - 2$ cho $B = {x^3} + 3{x^2} - 1$ .

a) Bằng cách đặt tính chia, hãy tìm thương và dư trong phép chia A cho B.

b) Em có cách nào không cần thực hiện phép chia mà vẫn tìm được đa thức dư hay không?

Phương pháp giải - Xem chi tiết

a) Muốn chia một đa thức cho một đa thức, ta đặt tính và tiến hành chia (tương tự phép chia hai số tự nhiên) cho đến khi nhận được đa thức dư hoặc đa thức không, hoặc có bậc nhỏ hơn bậc của đa thức chia.

b) Viết biểu thức A dưới dạng: $A = B.{x^2} + R\left( x \right)$ , khi đó R(x) là đa thức dư của phép chia A cho B.

Lời giải chi tiết

a) Ta đặt tính chia như sau:

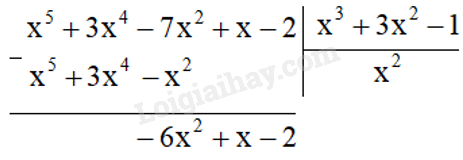
Vậy trong phép chia A cho B ta được thương là ${x^2}$ và dư là $- 6{x^2} + x - 2$ .

b) Không cần thực hiện phép chia, ta có thể tìm được thương và dư của phép chia này bằng cách biến đổi đa thức A như sau:

$A = {x^5} + 3{x^4} - 7{x^2} + x - 2$

$A = \left( {{x^5} + 3{x^4} - {x^2}} \right) - 6{x^2} + x - 2$ (vì $- 7{x^2} = - {x^2} - 6{x^2}$ )

$A = \left( {{x^3} + 3{x^2} - 1} \right){x^2} + \left( { - 6{x^2} + x - 2} \right)$ (vì ${x^5} + 3{x^4} - {x^2} = \left( {{x^3} + 3{x^2} - 1} \right){x^2}$ )

$A = B.{x^2} + \left( { - 6{x^2} + x - 2} \right)$

Trong đẳng thức cuối, đa thức $- 6{x^2} + x - 2$ có bậc 2 nhỏ hơn bậc của đa thức B.

Điều đó chứng tỏ ${x^2}$ là thương và $- 6{x^2} + x - 2$ là dư trong phép chia A cho B.

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 8 trang 49 vở thực hành Toán 7 tập 2
Cho đa thức (P = 6{x^3} + 5{x^2} + 4x + m) và (Q = 2{x^2} + x + 1). Tìm số m để phép chia P: Q là một phép chia hết.
Giải bài 6 (7.35) trang 48 vở thực hành Toán 7 tập 2
Bạn Tâm lúng túng khi muốn tìm thương và dư trong phép chia đa thức (21x - 4) cho (3{x^2}). Em có thể giúp bạn Tâm được không?
Giải bài 5 (7.34) trang 47, 48 vở thực hành Toán 7 tập 2
Trong mỗi trường hợp sau đây, tìm thương Q(x) và dư R(x) trong phép chia F(x) cho G(x) rồi biểu diễn F(x) dưới dạng: (Fleft( x right) = Gleft( x right).Qleft( x right) + Rleft( x right)). a) (Fleft( x right) = 6{x^4} - 3{x^3} + 15{x^2} + 2x - 1;Gleft( x right) = 3{x^2}). b) (Fleft( x right) = 12{x^4} + 10{x^3} - x - 3;Gleft( x right) = 3{x^2} + x + 1).
Giải bài 4 (7.33) trang 47 vở thực hành Toán 7 tập 2
Thực hiện phép chia (0,5{x^5} + 3,2{x^3} - 2{x^2}) cho (0,25{x^n}) trong mỗi trường hợp sau: a) (n = 2); b) (n = 3).
Giải bài 3 (7.32) trang 47 vở thực hành Toán 7 tập 2
Thực hiện các phép chia hai đa thức bằng cách đặt tính chia: a) (left( {6{x^3} - 2{x^2} - 9x + 3} right):left( {3x - 1} right)); b) (left( {4{x^4} + 14{x^3} - 21x - 9} right):left( {2{x^2} - 3} right)).
Giải bài 2 (7.31) trang 46, 47 vở thực hành Toán 7 tập 2
Thực hiện các phép chia đa thức sau: a) (left( { - 5{x^3} + 15{x^2} + 18x} right):left( { - 5x} right)); b) (left( { - 2{x^5} - 4{x^3} + 3{x^2}} right):2{x^2}).
Giải bài 1 (7.30) trang 46 vở thực hành Toán 7 tập 2
Tính: a) (8{x^5}:4{x^3}); b) (120{x^7}:left( { - 24{x^5}} right)); c) (frac{3}{4}{left( { - x} right)^3}:frac{1}{8}x); d) ( - 3,72{x^4}:left( { - 4{x^2}} right)).
Giải câu hỏi trắc nghiệm trang 46 vở thực hành Toán 7 tập 2
Cho hai đơn thức A và B có hệ số khác 0. Khi đó: A. A luôn chia hết cho B. B. A chia hết cho B nếu hệ số của A chia hết cho hệ số của B. C. A chia hết cho B nếu bậc của A nhỏ hơn bậc của B. D. A chia hết cho B nếu bậc của A không nhỏ hơn bậc của B.

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 7 - Kết nối tri thức - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

>> Học trực tuyến lớp 7 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều). Cam kết giúp học sinh lớp 7 học tốt, hoàn trả học phí nếu học không hiệu quả.