Giải bài 7 trang 25 vở thực hành Toán 9

Cho hệ phương trình (I) (left{ begin{array}{l} - 2x + y = 1\4x - 2y = 3end{array} right.). a) Giải hệ phương trình (I). b) Vẽ hai đường thẳng ( - 2x + y = 1) và (4x - 2y = 3) trên cùng một mặt phẳng tọa độ để minh họa kết luận ở câu a.

Đề bài

Cho hệ phương trình (I) \(\left\{ \begin{array}{l} - 2x + y = 1\\4x - 2y = 3\end{array} \right.\).

a) Giải hệ phương trình (I).

b) Vẽ hai đường thẳng \( - 2x + y = 1\) và \(4x - 2y = 3\) trên cùng một mặt phẳng tọa độ để minh họa kết luận ở câu a.

Phương pháp giải - Xem chi tiết

a) Giải phương trình bằng phương pháp cộng đại số.

b) Cách vẽ đường thẳng trên mặt phẳng tọa độ:

+ Xác định tọa độ hai điểm thuộc đường thẳng đó.

+ Vẽ đường thẳng đi qua hai điểm đó ta được đường thẳng cần tìm.

Lời giải chi tiết

a) Nhân hai vế phương trình thứ nhất với 2, ta được hệ phương trình \(\left\{ \begin{array}{l} - 4x + 2y = 2\\4x - 2y = 3\end{array} \right.\).

Cộng từng vế hai phương trình của hệ mới, ta được \(0x + 0y = 5\).

Do không có giá trị nào của x và y thỏa mãn hệ thức trên nên hệ phương trình đã cho vô nghiệm.

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

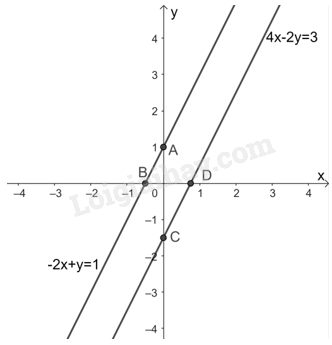
Giải bài 8 trang 26 vở thực hành Toán 9
Cho hệ phương trình (left{ begin{array}{l}3x - y = 1\ - 15x + my = - 7end{array} right.) Chứng tỏ rằng hệ phương trình đã cho vô nghiệm khi (m = 5).
Giải bài 9 trang 27 vở thực hành Toán 9
Tìm số tự nhiên n có hai chữ số, biết rằng nếu viết thêm chữ số 3 vào giữa hai chữ số của số n thì được một số lớn hơn số 2n là 585 đơn vị, và nếu viết hai chữ số của số n theo thứ tự ngược lại thì được một số nhỏ hơn số n là 18 đơn vị.
Giải bài 10 trang 27 vở thực hành Toán 9
Trên cánh đồng có diện tích 160ha của một đơn vị sản xuất, người ta dành 60ha để cấy thí điểm giống lúa mới, còn lại vẫn cấy giống lúa cũ. Khi thu hoạch, đầu tiên người ta gặt 8ha giống lúa cũ và 7ha giống lúa mới để đối chứng. Kết quả là 7ha giống lúa mới cho thu hoạch nhiều hơn 8ha giống lúa cũ là 2 tấn thóc. Biết rằng tổng số thóc (cả hai giống) thu hoạch cả vụ trên 160ha là 860 tấn. Hỏi năng suất của mỗi giống lúa trên 1ha là bao nhiêu tấn thóc?
Giải bài 11 trang 28 vở thực hành Toán 9
Hai vật chuyển động đều trên một đường tròn đường kính 20cm, xuất phát cùng một lúc, từ cùng một điểm. Nếu chuyển động ngược chiều thì cứ sau 4 giây chúng lại gặp nhau. Nếu chuyển động cùng chiều thì cứ 20 giây chúng lại gặp nhau. Tính vận tốc (cm/s) của mỗi vật.
Giải bài 12 trang 28 vở thực hành Toán 9
Một người mua hai loại hàng và phải trả tổng cộng là 21,7 triệu đồng, kể cả thuế giá trị gia tăng (VAT) với mức 10% đối với loại hàng thứ nhất và 8% đối với loại hàng thứ hai. Nếu thuế VAT là 9% đối với cả hai loại hàng thì người đó phải trả tổng cộng 21,8 triệu đồng. Hỏi nếu không kể thuế VAT thì người đó phải trả bao nhiêu tiền cho mỗi loại hàng?
Giải bài 6 trang 25 vở thực hành Toán 9
a) (left{ begin{array}{l}0,5x + 2y = - 2,5\0,7x - 3y = 8,1end{array} right.); b) (left{ begin{array}{l}5x - 3y = - 2\14x + 8y = 19end{array} right.); c) (left{ begin{array}{l}2left( {x - 2} right) + 3left( {1 + y} right) = - 2\3left( {x - 2} right) - 2left( {1 + y} right) = - 3end{array} right.).
Giải bài 5 trang 24 vở thực hành Toán 9
Giải các hệ phương trình: a) (left{ begin{array}{l}2x + 5y = 10\frac{2}{5}x + y = 1end{array} right.); b) (left{ begin{array}{l}0,2x + 0,1y = 0,3\3x + y = 5end{array} right.); c) (left{ begin{array}{l}frac{3}{2}x - y = frac{1}{2}\6x - 4y = 2end{array} right.).
Giải câu hỏi trắc nghiệm trang 24 vở thực hành Toán 9
Cặp số nào sau đây là nghiệm của hệ phương trình (left{ begin{array}{l}5x + 7y = - 13x + 2y = - 5end{array} right.)? A. (left( { - 1;1} right)). B. (left( { - 3;2} right)). C. (left( {2; - 3} right)). D. (left( {5;5} right)).