Giải bài 5 (9.24) trang 79 vở thực hành Toán 7 tập 2

Gọi BE và CF là hai đường phân giác của tam giác ABC cân tại A. Chứng minh (BE = CF).

Tổng hợp đề thi học kì 1 lớp 7 tất cả các môn - Kết nối tri thức

Toán - Văn - Anh - Khoa học tự nhiên...

Đề bài

Gọi BE và CF là hai đường phân giác của tam giác ABC cân tại A. Chứng minh \(BE = CF\).

Phương pháp giải - Xem chi tiết

Chứng minh \(\Delta BCE = \Delta CBF\left( {g.c.g} \right)\) suy ra \(BE = CF\).

Lời giải chi tiết

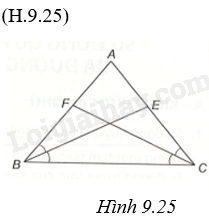
Tam giác ABC cân tại A nên \(\widehat {ABC} = \widehat {ACB}\).

Xét \(\Delta BCE\) và \(\Delta CBF\) có:

BC chung, \(\widehat {FBC} = \widehat {ECB}\), \(\widehat {EBC} = \frac{1}{2}\widehat {ABC} = \frac{1}{2}\widehat {ACB} = \widehat {FCB}\)

Do đó, \(\Delta BCE = \Delta CBF\left( {g.c.g} \right)\)

Suy ra \(BE = CF\).

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 6 trang 79 vở thực hành Toán 7 tập 2
Cho tam giác ABC vuông tại A có góc B bằng ({60^o}). Tia phân giác của góc ABC cắt AC ở E. Kẻ EM vuông góc với BC (left( {M in BC} right)). a) Chứng minh (Delta ABE = Delta MBE). b) Chứng minh (MB = MC). c) Gọi I là giao điểm của BA và ME. Chứng minh (IE > EM).
Giải bài 4 (9.23) trang 78 vở thực hành Toán 7 tập 2
Kí hiệu I là điểm đồng quy của ba đường phân giác trong tam giác ABC. Tính góc BIC khi biết góc BAC bằng 120o.
Giải bài 3 (9.22) trang 78 vở thực hành Toán 7 tập 2
Cho tam giác ABC có các đường trung tuyến BM và CN cắt nhau tại G. Biết góc GBC lớn hơn góc GCB. Hãy so sánh BM và CN.
Giải bài 2 (9.21) trang 77, 78 vở thực hành Toán 7 tập 2
Chứng minh rằng: a) Trong một tam giác cân, hai đường trung tuyến ứng với hai cạnh bên là hai đoạn thẳng bằng nhau. b) Ngược lại, nếu tam giác có hai đường trung tuyến bằng nhau thì tam giác đó cân.
Giải bài 1 (9.20) trang 77 vở thực hành Toán 7 tập 2
Cho tam giác ABC với hai đường trung tuyến BN, CP và trọng tâm G. Hãy tìm số thích hợp đặt vào dấu “?” để được các đẳng thức: (BG = ?BN,CG = ?CP,BG = ?GN,CG = ?GP).
Giải câu hỏi trắc nghiệm trang 76, 77 vở thực hành Toán 7 tập 2
Trong tam giác ABC, các đường trung tuyến AM, BN, CP đồng quy tại điểm G. Khi đó ta có: A. (frac{{GA}}{{MA}} = frac{1}{2}). B. (frac{{GB}}{{NG}} = frac{1}{2}). C. (frac{{GC}}{{PC}} = frac{2}{3}). D. (frac{{MA}}{{GA}} = frac{2}{3}).