Giải bài 4 (9.4) trang 67, 68 vở thực hành Toán 7 tập 2

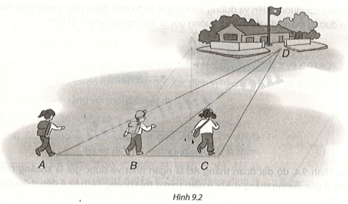
Ba bạn Mai, Việt và Hà đi đến trường tại địa điểm D lần lượt theo ba con đường AD, BD và CD (H.9.2). Biết rằng ba điểm A, B, C cùng nằm trên một đường thẳng, B nằm giữa A và C, (widehat {ACD}) là góc tù. Hỏi bạn nào đi xa nhất, bạn nào đi gần nhất? Vì sao?

Đề bài

Ba bạn Mai, Việt và Hà đi đến trường tại địa điểm D lần lượt theo ba con đường AD, BD và CD (H.9.2). Biết rằng ba điểm A, B, C cùng nằm trên một đường thẳng, B nằm giữa A và C, \(\widehat {ACD}\) là góc tù. Hỏi bạn nào đi xa nhất, bạn nào đi gần nhất? Vì sao?

Phương pháp giải - Xem chi tiết

Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn.

Lời giải chi tiết

Trong tam giác BDC có \(\widehat {ACD}\) là góc tù. Cạnh BD đối diện \(\widehat {ACD}\) nên BD là cạnh lớn nhất, suy ra \(BD > DC\). (1)

Tương tự, trong tam giác ABD có \(\widehat {ABD}\) là góc tù (vì \(\widehat {ABD}\) kề bù với góc nhọn \(\widehat {DBC}\)), cạnh AD đối diện với \(\widehat {ABD}\), suy ra \(AD > BD\). (2)

Từ (1) và (2), ta có \(AD > BD > DC\). Vậy bạn Mai đi xa nhất và bạn Hà đi gần nhất.

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 5 (9.5) trang 68 vở thực hành Toán 7 tập 2
Ba địa điểm A, B, C là ba đỉnh của một tam giác ABC với (widehat A) tù, (AC = 500m). Đặt một loa truyền thanh tại điểm nằm giữa A và B thì tại C có thể nghe tiếng loa không nếu bán kính để nghe rõ tiếng của loa là 500m?
Giải bài 3 trang 67 vở thực hành Toán 7 tập 2
Cho tam giác ABC có (widehat A:widehat B:widehat C = 5:4:6). Tính các góc của tam giác ABC, từ đó hãy so sánh độ dài ba cạnh của tam giác ABC.
Giải bài 2 (9.2) trang 67 vở thực hành Toán 7 tập 2
Trong Hình 9.1 có hai đoạn thẳng BC và DC bằng nhau, D nằm giữa A và C. Hỏi kết luận nào trong các kết luận sau là đúng? Tại sao? a) (widehat A = widehat B). b) (widehat A > widehat B). c) (widehat A < widehat B).
Giải bài 1 (9.1) trang 66 vở thực hành Toán 7 tập 2
Cho tam giác ABC có (widehat A = {105^o},widehat B = {35^o}). a) Tam giác ABC là tam giác gì? b) Tìm cạnh lớn nhất của tam giác ABC.
Giải câu hỏi trắc nghiệm trang 66 vở thực hành Toán 7 tập 2
Chọn phương án trả lời đúng trong mỗi câu sau: Cho tam giác ABC có (AB = 2cm,BC = 4cm,CA = 4,5cm). Khi đó: A. (widehat B < widehat A). B. (widehat A < widehat B < widehat C). C. (widehat A < widehat C < widehat B). D. (widehat C < widehat A < widehat B).