Giải bài 3 trang 92 vở thực hành Toán 9 tập 2

Cho tam giác ABC nội tiếp đường tròn (O). Gọi H là trực tâm của tam giác ABC. Chứng minh rằng (widehat {BAH} = widehat {OAC}).

Tổng hợp đề thi giữa kì 1 lớp 9 tất cả các môn - Kết nối tri thức

Toán - Văn - Anh - Khoa học tự nhiên

Đề bài

Cho tam giác ABC nội tiếp đường tròn (O). Gọi H là trực tâm của tam giác ABC. Chứng minh rằng \(\widehat {BAH} = \widehat {OAC}\).

Phương pháp giải - Xem chi tiết

+ Cho AH cắt BC tại D ta được tam giác ABD vuông tại D. Khi đó, \(\widehat {BAH} = {90^o} - \widehat {ABC}\).

+ \(\Delta AOC\) cân tại O nên: \(\widehat {OAC} = \widehat {OCA} = \frac{{{{180}^o} - \widehat {AOC}}}{2} = {90^o} - \frac{{\widehat {AOC}}}{2} = {90^o} - \widehat {ABC}\).

+ Do đó, \(\widehat {BAH} = \widehat {OAC}\).

Lời giải chi tiết

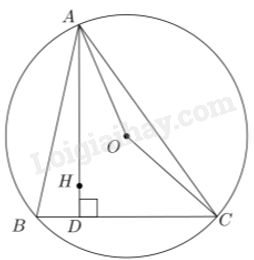
Cho AH cắt BC tại D ta được tam giác ABD vuông tại D. Khi đó, \(\widehat {BAH} = \widehat {BAD} = {90^o} - \widehat {ABD} = {90^o} - \widehat {ABC}\left( 1 \right)\)

Mặt khác, vì \(\Delta AOC\) cân tại O nên: \(\widehat {OAC} = \widehat {OCA} = \frac{{{{180}^o} - \widehat {AOC}}}{2} = {90^o} - \frac{{\widehat {AOC}}}{2} = {90^o} - \widehat {ABC}\;\left( 2 \right)\)

Từ (1), (2) suy ra: \(\widehat {BAH} = \widehat {OAC}\).

👉

Giải bài nhanh với AI Hay:

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 4 trang 92, 93 vở thực hành Toán 9 tập 2
Cho đường tròn (I) nội tiếp tam giác ABC với các tiếp điểm trên các cạnh AB, AC lần lượt là E, F. Chứng minh rằng (widehat {EIF} + widehat {BAC} = {180^o}).
Giải bài 5 trang 93 vở thực hành Toán 9 tập 2
Cho tam giác đều ABC ngoại tiếp đường tròn (I). Tính độ dài các cạnh của tam giác ABC biết rằng bán kính của (I) bằng 1cm.
Giải bài 6 trang 93 vở thực hành Toán 9 tập 2
Người ta muốn làm một khung gỗ tam giác đều để đặt vừa khít một chiếc đồng hồ hình tròn có đường kính 30cm như hình bên. Hỏi độ dài các cạnh (phía bên trong) của khung gỗ phải bằng bao nhiêu?
Giải bài 7 trang 93 vở thực hành Toán 9 tập 2
Cho tam giác ABC với độ dài ba cạnh là (AC = 1cm,AB = 2cm,BC = sqrt 5 cm). Hãy tính bán kính đường tròn ngoại tiếp và đường tròn nội tiếp tam giác ABC.
Giải bài 8 trang 94 vở thực hành Toán 9 tập 2
Cho tam giác ABC nội tiếp đường tròn (O). Trên các cạnh AB, AC lần lượt lấy các điểm M và N (M khác A và B, N khác A và C). Giả sử đường tròn ngoại tiếp tam giác AMN cắt đường tròn (O) tại một điểm S khác A. Chứng minh rằng (frac{{SM}}{{SB}} = frac{{SN}}{{SC}}).
Giải bài 2 trang 92 vở thực hành Toán 9 tập 2
Cho tam giác đều ABC nội tiếp đường tròn (O). Biết rằng đường tròn (O) có bán kính bằng 3cm. Tính diện tích tam giác ABC.
Giải bài 1 trang 92 vở thực hành Toán 9 tập 2
Cho đường tròn (O) ngoại tiếp tam giác ABC. Tính bán kính của (O), biết rằng ABC là tam giác vuông cân tại A và có cạnh bên bằng (2sqrt 2 cm).
Giải câu hỏi trắc nghiệm trang 91 vở thực hành Toán 9 tập 2
Khẳng định nào dưới đây là đúng? A. Tâm đường tròn ngoại tiếp một tam giác là giao điểm của ba đường phân giác. B. Tâm đường tròn nội tiếp một tam giác là giao điểm của ba đường trung trực. C. Tâm đường tròn nội tiếp một tam giác đều là trọng tâm của tam giác đó. D. Tâm đường tròn ngoại tiếp một tam giác vuông là trọng tâm của tam giác đó.