Giải bài 15 trang 100 sách bài tập toán 9 - Chân trời sáng tạo tập 1

Cho tam giác ABC cân tại A, (widehat A < {90^o}). Vẽ đường tròn đường kính AB cắt BC và AC lần lượt tại D và E. Chứng minh rằng: a) (Delta DBE) là tam giác cân. b) (widehat {CBE} = frac{1}{2}widehat {BAC})

Đề bài

Cho tam giác ABC cân tại A, \(\widehat A < {90^o}\). Vẽ đường tròn đường kính AB cắt BC và AC lần lượt tại D và E. Chứng minh rằng:

a) \(\Delta DBE\) là tam giác cân.

b) \(\widehat {CBE} = \frac{1}{2}\widehat {BAC}\)

Phương pháp giải - Xem chi tiết

Chứng minh DE = DB suy ra \(\Delta DBE\) là tam giác cân.

Hai góc nội tiếp cùng chắn một cung thì bằng nhau.

Lời giải chi tiết

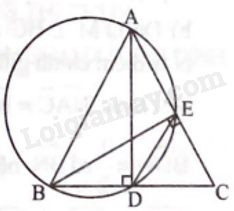
a) Ta có D, E cùng nằm trên đường tròn đường kính AB nên \(\widehat {ADB} = \widehat {AEB} = {90^o}\) hay \(AD \bot BC\) và \(BE \bot AC\).

Mà tam giác ABC cân tại A nên D là trung điểm BC nên DE = DB = DC. Vậy tam giác BDE cân tại D.

b) Ta có AD là tia phân giác của \(\widehat {CAB}\), nên \(\widehat {BAD} = \widehat {CAD} = \frac{1}{2}\widehat {CAB}\).

Mặt khác \(\widehat{CBE}=\widehat{DBE}=\widehat{EAD}=\frac{1}{2}sđ\overset\frown{DE}\).

Suy ra \(\widehat {CBE} = \widehat {BAD} = \frac{1}{2}\widehat {BAC}\).

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 16 trang 101 sách bài tập toán 9 - Chân trời sáng tạo tập 1
Trong Hình 9, cho biết AB = 12, AC = 16; đường tròn (I) tiếp xúc với AH, BC và đường tròn (O); đường tròn (J) tiếp xúc với AH, BC và đường tròn (O). Tính: a) BC, BH. b) Bán kính R, R’ của đường tròn (I) và (J). c) Khoảng cách PQ.
Giải bài 17 trang 101 sách bài tập toán 9 - Chân trời sáng tạo tập 1
Cho hai đường tròn (O; R) và (O’; R’) cắt nhau tại hai điểm A và B phân biệt. Vẽ đường thẳng vuông góc với AB tại A và cắt (O), (O’) lần lượt tại C, D. Tia CB cắt (O’) tại E, tia DB cắt (O) tại F. Chứng minh rằng: a) CD.CA = CB.CE. b) DC.DA = DB.DF. c) CD2 = CB.CE + DB.DF.
Giải bài 18 trang 101 sách bài tập toán 9 - Chân trời sáng tạo tập 1
Cho hai đường tròn (O; R) và (O’; R’) (R > R’) tiếp xúc trong tại A. Một tiếp tuyến của đường tròn (O’) tại M cắt đường tròn (O) tại hai điểm B, C. Đường thẳng BO’ cắt đường tròn (O) tại điểm thứ hai D và cắt đường thẳng AM tại E. Gọi F là giao điểm thứ hai của đường tròn ngoại tiếp tam giác ADE với AC và N là giao điểm thứ hai của AN với (O). Chứng minh rằng: a) O’M // ON. b) Ba điểm D, N, F thẳng hàng. c) DF là tia phân giác của góc (widehat {BDC}).
Giải bài 14 trang 100 sách bài tập toán 9 - Chân trời sáng tạo tập 1
Cho đường tròn (O; R) và một điểm M bên trong đường tròn đó. Qua M kẻ hai dây cung AB và CD vuông góc với nhau (D thuộc cung nhỏ AB). Vẽ đường kính DE. Chứng minh: a) MA.MB = MC.MD. b) Tứ giác ABEC là hình thang cân. c) Tổng MA2 + MB2 + MC2 + MD2 có giá trị không đổi khi M thay đổi vị trí trong đường tròn (O).
Giải bài 13 trang 100 sách bài tập toán 9 - Chân trời sáng tạo tập 1
Cho tam giác ABC nhọn với các đường cao AA’, BB’, CC’. Chứng minh rằng A’A là tia phân giác của góc (widehat {B'A'C'}).
Giải bài 12 trang 100 sách bài tập toán 9 - Chân trời sáng tạo tập 1
Cho AB và AC là hai tiếp tuyến tiếp xúc với đường tròn (O; R) lần lượt tại hai tiếp điểm B và C (Hình 8). a) AB = AO. b) Tia AO là tia phân giác của (widehat {BAC}). c) Tia OA là tai phân giác của (widehat {BOC}) d) OA = OB = R.
Giải bài 11 trang 100 sách bài tập toán 9 - Chân trời sáng tạo tập 1
Cho bốn điểm A, B, C, D trên đường tròn (O) như Hình 7. a) (widehat {BOC}) là góc nội tiếp chắn cung (oversetfrown{BC}) của đường tròn (O). b) (widehat {OBC} = {40^o}) c) (widehat {BAC} = widehat {BDC}) d) (widehat {BAC} = 70{}^o)
Giải bài 10 trang 100 sách bài tập toán 9 - Chân trời sáng tạo tập 1
Cho hai đường tròn C(O; 7 cm), C’(O’; 8 cm) và OO’ = 15 cm. a) Hai đường tròn (C) và (C’) cắt nhau. b) Hai đường tròn (C) và (C’) tiếp xúc ngoài. c) Hai đường tròn (C) và (C’) tiếp xúc trong. d) Hai đường tròn (C) và (C’) chỉ có một điểm chung duy nhất.
Giải bài 9 trang 99 sách bài tập toán 9 - Chân trời sáng tạo tập 1
Hình vành khuyên giới hạn bởi hai đường tròn (O; 5 cm) và (O’; 2 cm) có diện tích (lấy (pi ) theo máy tính và kết quả làm tròn đến hàng phần trăm) là A. 131,94 cm2 B. 18,84 cm2 C. 9,42 cm2 D. 65,97 cm2.
Giải bài 8 trang 99 sách bài tập toán 9 - Chân trời sáng tạo tập 1
Hình quạt tròn bán kính R = 100 cm ứng với cung 40o có diện tích (lấy (pi ) theo máy tính và kết quả làm tròn đến hàng phần trăm) là A. 34,91 cm2 B. 3490,66 cm2 C. 69,82 cm2 D. 6981,32 cm2.
Giải bài 7 trang 99 sách bài tập toán 9 - Chân trời sáng tạo tập 1
Cung 50o của một đường tròn đường kính d = 25 cm có độ dài (lấy (pi ) theo máy tính và kết quả làm tròn đến hàng phần trăm) là A. 43,64 cm B. 10,91 cm C. 21,82 cm D. 87,28 cm.
Giải bài 6 trang 99 sách bài tập toán 9 - Chân trời sáng tạo tập 1
Số đo (theta ) của (widehat {RBS}) trong Hình 6 là A. 83o B. 41,5o C. 34o D. 66o
Giải bài 5 trang 99 sách bài tập toán 9 - Chân trời sáng tạo tập 1
Cho biết DE là tiếp tuyến của đường tròn trong Hình 5. Số đo (theta ) của góc (widehat {BCE}) trong hình là A. 29o B. 61o C. 58o D. 32o
Giải bài 4 trang 99 sách bài tập toán 9 - Chân trời sáng tạo tập 1
Cho biết DE là tiếp tuyến của đường tròn trong Hình 4. Số đo (theta ) của góc (widehat {BAD}) trong hình là A. 28o B. 52o C. 56o D. 26o
Giải bài 3 trang 98 sách bài tập toán 9 - Chân trời sáng tạo tập 1
Cho biết (soversetfrown{AB}=soversetfrown{BC}=soversetfrown{CA}) và OB = R. Độ dài cạnh BC là: A. (Rsqrt 3 ) B. (frac{{Rsqrt 3 }}{2}) C. (Rsqrt 2 ) D. (frac{{Rsqrt 3 }}{3})
Giải bài 2 trang 98 sách bài tập toán 9 - Chân trời sáng tạo tập 1
Số đo góc (widehat {BAC}) trong Hình 2 là: A. 50o B. 70o C. 30o D. 60o
Giải bài 1 trang 98 sách bài tập toán 9 - Chân trời sáng tạo tập 1
Số đo góc (widehat {BAC}) trong Hình 1 là: A. 55o B. 32,5o C. 65o D. 25o