Giải bài 13 trang 100 sách bài tập toán 9 - Chân trời sáng tạo tập 1
Cho tam giác ABC nhọn với các đường cao AA’, BB’, CC’. Chứng minh rằng A’A là tia phân giác của góc (widehat {B'A'C'}).
Đề bài
Cho tam giác ABC nhọn với các đường cao AA’, BB’, CC’. Chứng minh rằng A’A là tia phân giác của góc \(\widehat {B'A'C'}\).
Phương pháp giải - Xem chi tiết
Chứng minh bốn điểm B, A’, H, C’ cùng nằm trên một đường tròn
Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến.
Lời giải chi tiết
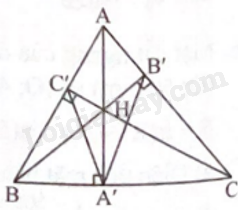
Gọi H là trực tâm của tam giác ABC.
Ta có \(\widehat {BC'H} = \widehat {BA'H} = {90^o}\), nên bốn điểm B, A’, H, C’ cùng nằm trên một đường tròn.
Do đó \(\widehat {HA'C'} = \widehat {HBC'}\).
Chứng minh tương tự, ta cũng có \(\widehat {HA'B'} = \widehat {HCB'}\).
Mà \(\widehat {HBC'} = \widehat {HCB'}\) (cùng phụ với \(\widehat {BAC}\)), nên ta có \(\widehat {C'A'H} = \widehat {B'A'H}\).
Từ đó, ta có A’A là tia phân giác của góc \(\widehat {B'A'C'}\).
- Giải bài 14 trang 100 sách bài tập toán 9 - Chân trời sáng tạo tập 1
- Giải bài 15 trang 100 sách bài tập toán 9 - Chân trời sáng tạo tập 1
- Giải bài 16 trang 101 sách bài tập toán 9 - Chân trời sáng tạo tập 1
- Giải bài 17 trang 101 sách bài tập toán 9 - Chân trời sáng tạo tập 1
- Giải bài 18 trang 101 sách bài tập toán 9 - Chân trời sáng tạo tập 1
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 9 - Chân trời sáng tạo - Xem ngay
Các bài khác cùng chuyên mục
- Giải bài 4 trang 86 sách bài tập toán 9 - Chân trời sáng tạo tập 2
- Giải bài 1 trang 98 sách bài tập toán 9 - Chân trời sáng tạo tập 2
- Giải bài 16 trang 109 sách bài tập toán 9 - Chân trời sáng tạo tập 2
- Giải bài 15 trang 109 sách bài tập toán 9 - Chân trời sáng tạo tập 2
- Giải bài 14 trang 109 sách bài tập toán 9 - Chân trời sáng tạo tập 2
- Giải bài 16 trang 109 sách bài tập toán 9 - Chân trời sáng tạo tập 2
- Giải bài 15 trang 109 sách bài tập toán 9 - Chân trời sáng tạo tập 2
- Giải bài 14 trang 109 sách bài tập toán 9 - Chân trời sáng tạo tập 2
- Giải bài 13 trang 109 sách bài tập toán 9 - Chân trời sáng tạo tập 2
- Giải bài 12 trang 108 sách bài tập toán 9 - Chân trời sáng tạo tập 2













Danh sách bình luận