Giải bài 11 trang 96 SGK Toán 8 – Cánh diều

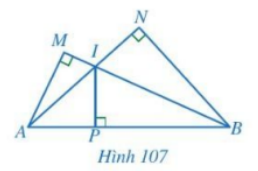
Cho Hình 107, chứng minh:

Đã có lời giải SGK Toán lớp 9 - Cánh diều (mới)

Đầy đủ - Chi tiết - Chính xác

Đề bài

Cho Hình 107, chứng minh:

a) \(\Delta ABN \backsim \Delta AIP\) và \(AI.AN = AP.AB\)

b) \(AI.AN + BI.BM = A{B^2}\)

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

a) Chứng minh hai tam giác đồng dạng theo trường hợp đồng dạng thứ ba.

b) Chứng minh \(\Delta AMB \backsim \Delta IPB\), suy ra tỉ số đồng dạng rồi thay vào biểu thức cần chứng minh.

Lời giải chi tiết

a) Xét tam giác ABN và tam giác AIP có:

\(\widehat {ANB} = \widehat {API} = 90^\circ \) và \(\widehat A\) chung

\( \Rightarrow \)\(\Delta ABN \backsim \Delta AIP\) (g-g)

\( \Rightarrow \frac{{AB}}{{AI}} = \frac{{AN}}{{AP}} \Rightarrow AI.AN = AP.AB\)

b) Xét tam giác AMB và tam giác IPB có:

\(\widehat {AMB} = \widehat {IPB} = 90^\circ \) và \(\widehat B\) chung

\( \Rightarrow \)\(\Delta AMB \backsim \Delta IPB\) (g-g)

\( \Rightarrow \frac{{AB}}{{BI}} = \frac{{BM}}{{BP}} \Rightarrow BI.BM = AP.PB\)

Khi đó:

\(AI.AN + BI.BM = AP.AB + AB.PB = AB\left( {AP + PB} \right) = A{B^2}\)

Bình luận

Chia sẻ

Bình chọn:

3.6 trên 5 phiếu

Bài tiếp theo

Giải bài 12 trang 96 SGK Toán 8 – Cánh diều
Sau một thời gian sử dụng, một tủ sách nghệ thuật đã có dấu hiệu bị xuống cấp và cần sửa lại (Hình 108).
Giải bài 13 trang 96 SGK Toán 8 – Cánh diều
Cho Hình 109. Hình nào đồng dạng phối cảnh với: a) Tam giác OAB? b) Tam giác OBC? c) Tam giác OCD? d) Tứ giác ABCD?
Giải bài 14 trang 96 SGK Toán 8 – Cánh diều
Hình 110 có ghi thứ tự của 6 lá mầm, trong đó có nhiều cặp lá mầm gợi nên những cặp hình đồng dạng. Hãy viết 6 cặp lá mầm gợi nên những hình đồng dạng.
Giải bài 10 trang 96 SGK Toán 8 – Cánh diều
Cho tam giác ABC có M, N là hai điểm lần lượt thuộc các cạnh AB, AC sao cho
Giải bài 9 trang 95 SGK Toán 8 – Cánh diều
Cho Hình 106. Chứng minh
Giải bài 8 trang 95 SGK Toán 8 – Cánh diều
Cho Hình 105. Chứng minh:
Giải bài 7 trang 95 SGK Toán 8 – Cánh diều
Tính các độ dài x, y, z, t ở các hình 104a, 104b, 104c.
Giải bài 6 trang 95 SGK Toán 8 – Cánh diều
Cho tam giác ABC đồng dạng với tam giác A'B'C' theo tỉ số đồng dạng
Giải bài 5 trang 94 SGK Toán 8 – Cánh diều
Cho hình bình hành ABCD. Gọi M, N, P lần lượt là trung điểm của các đoạn thẳng AB, BC, AN và Q là giao điểm của AN và DM. Chứng minh:
Giải bài 4 trang 94 SGK Toán 8 – Cánh diều
Cho tứ giác ABCD. Tia phân giác của các góc BAD và BCD cắt nhau tại điểm I
Giải bài 3 trang 94 SGK Toán 8 – Cánh diều
Cho tam giác ABC, các điểm M, N, P lần lượt thuộc các cạnh AB, AC, BC
Giải bài 2 trang 94 SGK Toán 8 – Cánh diều
Cho
Giải bài 1 trang 94 SGK Toán 8 – Cánh diều
Cho