Đề thi học kì 2 Toán 9 - Đề số 1
Phần I. Câu hỏi trắc nghiệm nhiều phương án lựa chọn (3 điểm) Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Đề bài
Hàm số nào dưới đây có đồ thị nằm hoàn toàn phía dưới trục hoành?
-
A.
\(y = 2x + 4\).
-
B.
\(y = 2{x^2}\).
-
C.
\(y = - 2{x^2}\).
-
D.
\(y = - 2x + 4\).
Phương trình \({x^2} - 6x + 1 - 3m = 0\) (với m là tham số) có nghiệm là -1 khi
-
A.
\(m = \frac{{ - 4}}{3}\).
-
B.
\(m = \frac{4}{3}\).
-
C.
\(m = \frac{8}{3}\).
-
D.
\(m = \frac{{ - 8}}{3}\).
Nếu hai số có tổng S = –5 và tích P = –14 thì hai số đó là nghiệm của phương trình:
-
A.
\({x^2} + 5x + 14 = 0\).
-
B.
\({x^2} - 5x + 14 = 0\).
-
C.
\({x^2} + 5x - 14 = 0\).
-
D.
\({x^2} - 5x - 14 = 0\).
Khảo sát các bạn học sinh khối 9 của một trường THCS về thời gian sử dụng mạng xã hội trung bình trong một ngày (đơn vị: giờ) thu được kết quả như biểu đồ tần số ghép nhóm sau:
Có bao nhiêu bạn tham gia khảo sát? Biết rằng có 4 bạn sử dụng mạng xã hội từ 4,5 giờ trở lên.
-
A.
50.
-
B.
40.
-
C.
100.
-
D.
46.
Xét phép thử “Gieo một đồng xu hai lần liên tiếp”. Số phần tử của không gian mẫu là
-
A.
\(1\).
-
B.
\(2\).
-
C.
\(3\).
-
D.
\(4\).
Cho tam giác ABC vuông tại A, có \(AB = 3\) cm, \(AC = 4\) cm. Độ dài của bán kính đường tròn ngoại tiếp tam giác ABC là
-
A.
\(5cm\).
-
B.
\(2cm\).
-
C.
\(3,5cm\).
-
D.
\(2,5cm\).
Trong các phát biểu sau phát biểu nào sai?
-
A.
Hình vuông nội tiếp đường tròn.
-
B.
Mọi tứ giác đều nội tiếp đường tròn.
-
C.
Hình chữ nhật là tứ giác nội tiếp.
-
D.
Tổng số đo hai góc đối trong tứ giác nội tiếp bằng \(180^\circ \).
Cho lục giác đều ABCDEF nội tiếp đường tròn bán kính 5. Độ dài cạnh AB bằng:
-
A.
5.
-
B.
\(5\sqrt 3 \).
-
C.
\(\frac{{5\sqrt 3 }}{2}\).
-
D.
\(\frac{{5\sqrt 3 }}{6}\).
Phép quay bao nhiêu độ sẽ giữ nguyên mọi điểm?
-
A.
\(0^\circ \).
-
B.
\(90^\circ \).
-
C.
\(100^\circ \).
-
D.
\(180^\circ \).
Cho hình chữ nhật có chiều dài 3cm, chiều rộng 2cm. Quay hình chữ nhật đó một vòng quanh chiều dài của nó ta được một hình trụ có diện tích xung quanh bằng
-
A.
\(6\pi \)\(\left( {c{m^2}} \right)\).
-
B.
\(8\pi \)\(\left( {c{m^2}} \right)\).
-
C.
\(12\pi \)\(\left( {c{m^2}} \right)\).
-
D.
\(18\pi \)\(\left( {c{m^2}} \right)\).
Cho hình nón có độ dài đường sinh là \(5\), bán kính đáy là \(3\). Diện tích toàn phần của hình nón bằng:
-
A.
\(15\pi \).
-
B.
\(48\pi \).
-
C.
\(39\pi \).
-
D.
\(24\pi \).
Một mặt phẳng đi qua tâm hình cầu, cắt hình cầu theo một hình tròn có diện tích \(9\pi c{m^2}.\) Thể tích của hình cầu bằng
-
A.
$927\pi c{{m}^{3}}$.
-
B.
$36\pi c{{m}^{3}}$.
-
C.
$6\pi c{{m}^{3}}$.
-
D.
$81\pi c{{m}^{3}}$.
Quãng đường AB dài \(90km\). Một ô tô đi từ A đến B với vận tốc và thời gian dự định. Thực tế sau khi đi được \(\frac{1}{3}\) quãng đường AB với vận tốc dự định thì ô tô đó nghỉ lại \(20\) phút. Vì vậy để đến đúng dự định, trên quãng đường còn lại ô tô phải tăng vận tốc thêm \(6km/h\).
a) Quãng đường còn lại sau khi ô tô nghỉ là \(60km\).
b) Gọi vận tốc dự định của ô tô là \(x\left( {km/h,{\rm{ }}x > 0} \right)\) thì thời gian ô tô đi hết \(\frac{1}{3}\) quãng đường đầu là \(30x\left( h \right)\).
c) Vận tốc dự định của ô tô bằng \(30km/h\).
d) Thời gian ô tô đi hết quãng đường còn lại là \(2,5h\).
Một ly nước có dạng hình trụ với bán kính đáy 4 cm và chiều cao 12 cm. Hiện tại, ly đang chứa nước với mực nước cao 7 cm. (lấy \(\pi \approx 3,14\), làm tròn kết quả đến hàng đơn vị)
a) Chiếc ly có thể chứa tối đa 600 ml nước.
b) Thể tích nước hiện tại trong ly khoảng 352 ml.
c) Nếu thả một viên bi sắt dạng hình cầu có đường kính 5 cm vào ly thì nước không tràn ra ngoài.
d) Nếu thả một viên bi sắt dạng hình cầu có đường kính 6 cm vào ly thì nước sẽ tràn ra ngoài.
Phương trình \(\frac{{2x}}{{x - 2}} - \frac{5}{{x - 3}} = \frac{{ - 9}}{{{x^2} - 5x + 6}}\) \(\left( {x \ne 2;x \ne 3} \right)\) có bao nhiêu nghiệm?
Đáp án:
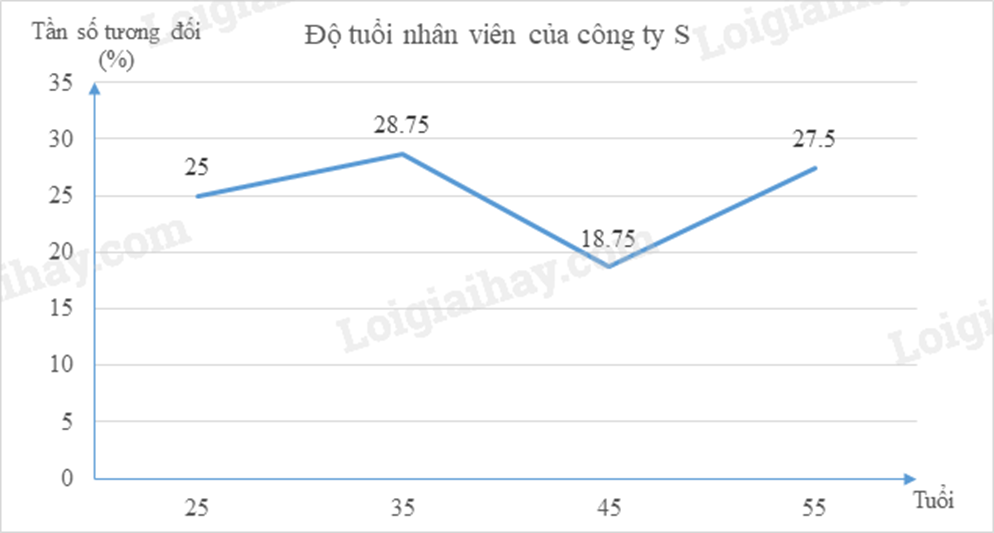
Khảo sát độ tuổi nhân viên của công ty S được chia ra làm 4 nhóm chính: từ 20 tuổi đến dưới 30 tuổi, từ 30 tuổi đến dưới 40 tuổi, từ 40 tuổi đến dưới 50 tuổi và từ 50 tuổi đến dưới 60 tuổi và kết quả được biểu diễn qua biểu đồ đoạn thẳng như hình vẽ dưới đây. Biết tổng số nhân viên có độ tuổi từ 20 đến dưới 40 tuổi là 430 người. Tính số nhân viên có độ tuổi từ 20 đến dưới 30 tuổi.
Đáp án:
Một nhóm bạn có 4 bạn gồm 2 bạn nam là Hiếu, An và hai bạn nữ là Linh, Ngọc. Chọn ngẫu nhiên 2 bạn để tham gia lao động. Số phần tử của không gian mẫu bằng bao nhiêu?
Đáp án:
Cạnh của một ngũ giác đều nội tiếp đường tròn bán kính \(4cm\) (làm tròn đến chữ số thập phân thứ nhất) là bao nhiêu cm?
Đáp án:
Lời giải và đáp án
Hàm số nào dưới đây có đồ thị nằm hoàn toàn phía dưới trục hoành?
-
A.
\(y = 2x + 4\).
-
B.
\(y = 2{x^2}\).
-
C.
\(y = - 2{x^2}\).
-
D.
\(y = - 2x + 4\).
Đáp án : C
Hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) nằm dưới trục hoành nếu \(a < 0\).
Đồ thị hàm số \(y = 2x + 4\) và \(y = - 2x + 4\) không nằm hoàn toàn phía dưới trục hoành.
Hàm số \(y = 2{x^2}\) có a = 2 > 0 nên đồ thị nằm hoàn toàn phía trên trục hoành.
Hàm số \(y = - 2{x^2}\) có a = -2 < 0 nên đồ thị nằm hoàn toàn phía dưới trục hoành.
Đáp án C
Phương trình \({x^2} - 6x + 1 - 3m = 0\) (với m là tham số) có nghiệm là -1 khi
-
A.
\(m = \frac{{ - 4}}{3}\).
-
B.
\(m = \frac{4}{3}\).
-
C.
\(m = \frac{8}{3}\).
-
D.
\(m = \frac{{ - 8}}{3}\).
Đáp án : C
Phương trình \(a{x^2} + bx + c = 0\) \((a \ne 0)\) có nghiệm là \({x_0}\) nếu \(a{x_0}^2 + b{x_0} + c = 0\).
Thay \(x = {x_0}\) vào phương trình \(a{x^2} + bx + c = 0\) để tìm m.
Thay \(x = - 1\) vào phương trình, ta được:
\(\begin{array}{l}{\left( { - 1} \right)^2} - 6.\left( { - 1} \right) + 1 - 3m = 0\\1 + 6 + 1 - 3m = 0\\3m = 8\\m = \frac{8}{3}\end{array}\)
Vậy \(m = \frac{8}{3}\).
Đáp án C
Nếu hai số có tổng S = –5 và tích P = –14 thì hai số đó là nghiệm của phương trình:
-
A.
\({x^2} + 5x + 14 = 0\).
-
B.
\({x^2} - 5x + 14 = 0\).
-
C.
\({x^2} + 5x - 14 = 0\).
-
D.
\({x^2} - 5x - 14 = 0\).
Đáp án : C
Nếu hai số có tổng bằng S và tích bằng P thì hai số đó là hai nghiệm của phương trình bậc hai:
\({x^2} - Sx + P = 0\)
Hai số có tổng S = –5 và tích P = –14 thì hai số đó là nghiệm của phương trình \({x^2} + 5x - 14 = 0\).
Đáp án C
Khảo sát các bạn học sinh khối 9 của một trường THCS về thời gian sử dụng mạng xã hội trung bình trong một ngày (đơn vị: giờ) thu được kết quả như biểu đồ tần số ghép nhóm sau:
Có bao nhiêu bạn tham gia khảo sát? Biết rằng có 4 bạn sử dụng mạng xã hội từ 4,5 giờ trở lên.
-
A.
50.
-
B.
40.
-
C.
100.
-
D.
46.
Đáp án : C
Xác định tần số tương đối tương ứng với số bạn sử dụng mạng xã hội từ 4,5 giờ trở lên.
Từ đó tính được số bạn tham gia khảo sát theo công thức tìm một số a khi biết giá trị m% của nó bằng b:
\(a = b:m\% \)
Tần số tương đối tương ứng với số bạn sử dụng mạng xã hội từ 4,5 giờ trở lên là 4%.
Suy ra số bạn tham gia khảo sát là: \(4:4\% = 100\) (bạn)
Đáp án C
Xét phép thử “Gieo một đồng xu hai lần liên tiếp”. Số phần tử của không gian mẫu là
-
A.
\(1\).
-
B.
\(2\).
-
C.
\(3\).
-
D.
\(4\).
Đáp án : D
Xác định các phần tử của không gian mẫu.
Không gian mẫu của phép thử là: \(\Omega = \left\{ {SS,SN,NS,NN} \right\}\).
Số phần tử của không gian mẫu là 4.
Đáp án D
Cho tam giác ABC vuông tại A, có \(AB = 3\) cm, \(AC = 4\) cm. Độ dài của bán kính đường tròn ngoại tiếp tam giác ABC là
-
A.
\(5cm\).
-
B.
\(2cm\).
-
C.
\(3,5cm\).
-
D.
\(2,5cm\).
Đáp án : D
Tính cạnh huyền của tam giác bằng định lí Pythagore.
Bán kính đường tròn ngoại tiếp tam giác vuông bằng một nửa cạnh huyền.
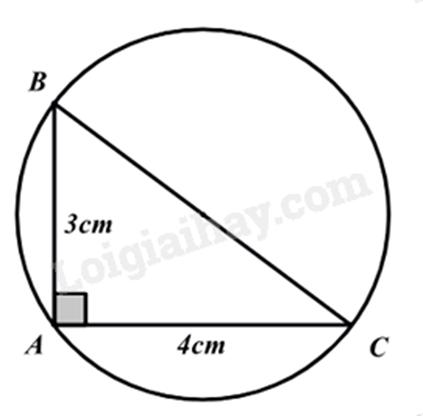
Áp dụng định lí Pythagore vào tam giác ABC vuông tại A, ta có:
\(B{C^2} = A{B^2} + A{C^2} = {3^2} + {4^2} = 25\) suy ra \(BC = \sqrt {25} = 5\left( {cm} \right)\)
Do đó độ dài bán kính đường tròn ngoại tiếp tam giác ABC là: \(\frac{5}{2} = 2,5\left( {cm} \right)\).
Đáp án D
Trong các phát biểu sau phát biểu nào sai?
-
A.
Hình vuông nội tiếp đường tròn.
-
B.
Mọi tứ giác đều nội tiếp đường tròn.
-
C.
Hình chữ nhật là tứ giác nội tiếp.
-
D.
Tổng số đo hai góc đối trong tứ giác nội tiếp bằng \(180^\circ \).
Đáp án : B
Dựa vào các kiến thức về tứ giác nội tiếp.
A. Hình vuông nội tiếp đường tròn là khẳng định đúng.
B. Mọi tứ giác đều nội tiếp đường tròn là khẳng định sai vì không phải tứ giác nào cũng nội tiếp đường tròn.
C. Hình chữ nhật là tứ giác nội tiếp là khẳng định đúng.
D. Tổng số đo hai góc đối trong tứ giác nội tiếp bằng \(180^\circ \) là khẳng định đúng theo tính chất tổng hai góc đối của tứ giác nội tiếp.
Đáp án B
Cho lục giác đều ABCDEF nội tiếp đường tròn bán kính 5. Độ dài cạnh AB bằng:
-
A.
5.
-
B.
\(5\sqrt 3 \).
-
C.
\(\frac{{5\sqrt 3 }}{2}\).
-
D.
\(\frac{{5\sqrt 3 }}{6}\).
Đáp án : A
Chia hình lục giác đều thành 6 tam giác đều thì ta tính được cạnh của lục giác đều.
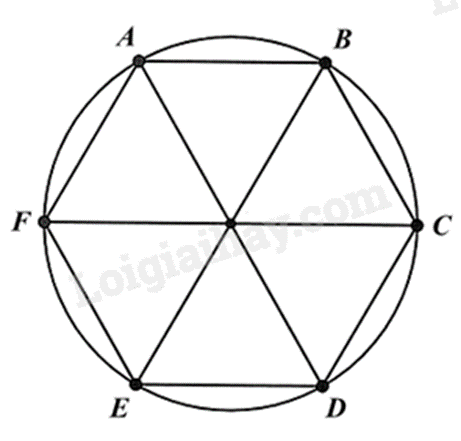
Lục giác đều chia thành 6 tam giác đều bằng nhau nên mỗi cạnh của tam giác có độ dài bằng bán kính.
Do đó AB = 5 (= bán kính).
Đáp án A
Phép quay bao nhiêu độ sẽ giữ nguyên mọi điểm?
-
A.
\(0^\circ \).
-
B.
\(90^\circ \).
-
C.
\(100^\circ \).
-
D.
\(180^\circ \).
Đáp án : A
Sử dụng kiến thức: Phép quay 0° và phép quay 360° giữ nguyên mọi điểm.
Vì phép quay 0° và phép quay 360° giữ nguyên mọi điểm nên ta chọn đáp án A.
Đáp án A
Cho hình chữ nhật có chiều dài 3cm, chiều rộng 2cm. Quay hình chữ nhật đó một vòng quanh chiều dài của nó ta được một hình trụ có diện tích xung quanh bằng
-
A.
\(6\pi \)\(\left( {c{m^2}} \right)\).
-
B.
\(8\pi \)\(\left( {c{m^2}} \right)\).
-
C.
\(12\pi \)\(\left( {c{m^2}} \right)\).
-
D.
\(18\pi \)\(\left( {c{m^2}} \right)\).
Đáp án : C
Xác định chiều cao và bán kính đáy của hình trụ tạp thành.
Sử dụng công thức tính diện tích xung quanh của hình trụ: \({S_{xq}} = 2\pi rh\)
Ta có hình vẽ:
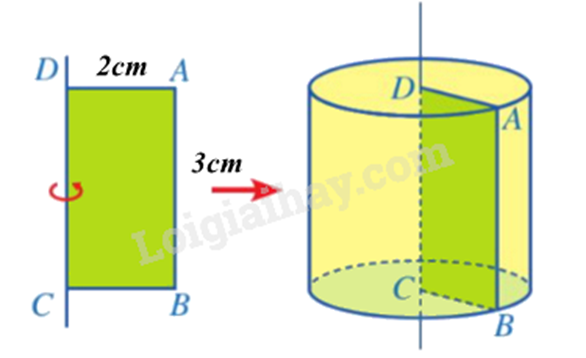
Qua hình vẽ ta thấy hình trụ được sinh ra có chiều cao h = 3 cm và bán kính đáy r = 2 cm.
Diện tích xung quanh của hình trụ là: \({S_{xq}} = 2\pi .2.3 = 12\pi \left( {c{m^2}} \right)\)
Đáp án C
Cho hình nón có độ dài đường sinh là \(5\), bán kính đáy là \(3\). Diện tích toàn phần của hình nón bằng:
-
A.
\(15\pi \).
-
B.
\(48\pi \).
-
C.
\(39\pi \).
-
D.
\(24\pi \).
Đáp án : D
Sử dụng công thức tính diện tích toàn phần của hình nón: ${{S}_{tp}}={{S}_{xq}}+{{S}_{đáy}}=\pi rl+\pi {{r}^{2}}$.
Diện tích toàn phần của hình nón là:
${{S}_{tp}}={{S}_{xq}}+{{S}_{đáy}}=\pi .3.5+\pi {{.3}^{2}}=15\pi +9\pi =24\pi $.
Đáp án D
Một mặt phẳng đi qua tâm hình cầu, cắt hình cầu theo một hình tròn có diện tích \(9\pi c{m^2}.\) Thể tích của hình cầu bằng
-
A.
$927\pi c{{m}^{3}}$.
-
B.
$36\pi c{{m}^{3}}$.
-
C.
$6\pi c{{m}^{3}}$.
-
D.
$81\pi c{{m}^{3}}$.
Đáp án : B
Dựa vào diện tích hình tròn ta tính được bán kính của hình cầu: \(S = \pi {r^2}\).
Sử dụng công thức tính thể tích hình cầu: \(V = \frac{4}{3}\pi {r^3}\).
Vì diện tích của hình tròn là \(9\pi c{m^2}\) nên ta có: \(\pi {r^2} = 9\pi \)
Suy ra bán kính của hình cầu là: \(r = \sqrt 9 = 3\left( {cm} \right)\)
Do đó thể tích của hình cầu là: \(V = \frac{4}{3}\pi {r^3} = \frac{4}{3}\pi {.3^3} = 36\pi \left( {c{m^3}} \right)\)
Đáp án B
Quãng đường AB dài \(90km\). Một ô tô đi từ A đến B với vận tốc và thời gian dự định. Thực tế sau khi đi được \(\frac{1}{3}\) quãng đường AB với vận tốc dự định thì ô tô đó nghỉ lại \(20\) phút. Vì vậy để đến đúng dự định, trên quãng đường còn lại ô tô phải tăng vận tốc thêm \(6km/h\).
a) Quãng đường còn lại sau khi ô tô nghỉ là \(60km\).
b) Gọi vận tốc dự định của ô tô là \(x\left( {km/h,{\rm{ }}x > 0} \right)\) thì thời gian ô tô đi hết \(\frac{1}{3}\) quãng đường đầu là \(30x\left( h \right)\).
c) Vận tốc dự định của ô tô bằng \(30km/h\).
d) Thời gian ô tô đi hết quãng đường còn lại là \(2,5h\).
a) Quãng đường còn lại sau khi ô tô nghỉ là \(60km\).
b) Gọi vận tốc dự định của ô tô là \(x\left( {km/h,{\rm{ }}x > 0} \right)\) thì thời gian ô tô đi hết \(\frac{1}{3}\) quãng đường đầu là \(30x\left( h \right)\).
c) Vận tốc dự định của ô tô bằng \(30km/h\).
d) Thời gian ô tô đi hết quãng đường còn lại là \(2,5h\).
a) Tính quãng đường ô tô đã đi = \(\frac{1}{3}\). quãng đường AB.
Quãng đường còn lại sau khi ô tô nghỉ = quãng đường AB – quãng đường đã đi.
b) Sử dụng công thức: Thời gian = Quãng đường : Vận tốc
c) Gọi vận tốc dự định của ô tô là \(x\left( {km/h,{\rm{ }}x > 0} \right)\)
Biểu diễn vận tốc ô tô đi quãng đường còn lại sau khi ô tô nghỉ theo x
Biểu diễn thời gian ô tô dự định và thực tế ô tô đi.
Vì thời gian dự định và thời gian thực tế ô tô đi là như nhau nên ta lập được phương trình.
Giải phương trình tìm x. Kiểm tra lại điều kiện.
d) Thay giá trị x vừa tìm được vào công thức biểu diễn thời gian ô tô đi hết quãng đường còn lại.
a) Đúng
Quãng đường ô tô đã đi là: \(90.\frac{1}{3} = 30\left( {km} \right)\)
Quãng đường còn lại sau khi ô tô nghỉ là: \(90 - 30 = 60\left( {km} \right)\)
b) Sai
Thời gian ô tô đi hết \(\frac{1}{3}\) quãng đường đầu là: \(\frac{{30}}{x}\) (h)
c) Đúng
Gọi vận tốc dự định của ô tô là \(x\left( {km/h,{\rm{ }}x > 0} \right)\)
Vận tốc ô tô đi quãng đường còn lại sau khi ô tô nghỉ là: \(x + 6\left( {km/h} \right)\)
Thời gian ô tô dự định đi là: \(\frac{{90}}{x}\) (h)
Thực tế:
+) Thời gian ô tô đi hết \(\frac{1}{3}\) quãng đường đầu là: \(\frac{{30}}{x}\) (h)
+) Thời gian ô tô nghỉ là: 20 phút = \(\frac{1}{3}\) h
+) Thời gian ô tô đi quãng đường còn lại là: \(\frac{{60}}{{x + 6}}\) (h)
Vì thời gian dự định và thời gian thực tế ô tô đi là như nhau nên ta có phương trình:
\(\frac{{90}}{x} = \frac{{30}}{x} + \frac{1}{3} + \frac{{60}}{{x + 6}}\)
\(\frac{{60}}{x} - \frac{{60}}{{x + 6}} - \frac{1}{3} = 0\)
\(\begin{array}{l}60.3.\left( {x + 6} \right) - 60.3.x - x\left( {x + 6} \right) = 0\\180x + 1080 - 180x - {x^2} - 6x = 0\\ - {x^2} - 6x + 1080 = 0\end{array}\)
Giải phương trình ta được: \({x_1} = 30\left( {TM} \right);{x_2} = - 36\left( {KTM} \right)\).
Vậy vận tốc dự định của ô tô là 30km/h.
d) Sai
Thời gian ô tô đi hết quãng đường còn lại là:
\(\frac{{60}}{{30 + 6}} = \frac{5}{3} \approx 1,67\left( h \right) \ne 2,5\left( h \right)\)
Đáp án: ĐSĐS
Một ly nước có dạng hình trụ với bán kính đáy 4 cm và chiều cao 12 cm. Hiện tại, ly đang chứa nước với mực nước cao 7 cm. (lấy \(\pi \approx 3,14\), làm tròn kết quả đến hàng đơn vị)
a) Chiếc ly có thể chứa tối đa 600 ml nước.
b) Thể tích nước hiện tại trong ly khoảng 352 ml.
c) Nếu thả một viên bi sắt dạng hình cầu có đường kính 5 cm vào ly thì nước không tràn ra ngoài.
d) Nếu thả một viên bi sắt dạng hình cầu có đường kính 6 cm vào ly thì nước sẽ tràn ra ngoài.
a) Chiếc ly có thể chứa tối đa 600 ml nước.
b) Thể tích nước hiện tại trong ly khoảng 352 ml.
c) Nếu thả một viên bi sắt dạng hình cầu có đường kính 5 cm vào ly thì nước không tràn ra ngoài.
d) Nếu thả một viên bi sắt dạng hình cầu có đường kính 6 cm vào ly thì nước sẽ tràn ra ngoài.
a) Lượng nước có thể chứa tối đa chính là thể tích của ly nước: \(V = \pi {r^2}h\).
b) Tính thể tích nước trong ly: \(V = \pi {r^2}h\) (h là chiều cao mực nước)
c, d) Tính thể tích viên bi sắt: \({V_{bi}} = \frac{4}{3}\pi {r^3}\).
a) Sai
Lượng nước có thể chứa tối đa chính là thể tích của ly nước.
Chiếc ly có thể chứa tối đa lượng nước là:
\(V = \pi {r^2}h = 3,{14.4^2}.12 \approx 603\left( {c{m^3}} \right) = 603\left( {ml} \right)\)
b) Đúng
Thể tích nước hiện tại trong ly là:
\({V_{nc}} = \pi {r^2}h = 3,{14.4^2}.7 \approx 352\left( {c{m^3}} \right) = 352\left( {ml} \right)\)
c) Đúng
Bán kính viên bi sắt là: \(\frac{5}{2} = 2,5\left( {cm} \right)\)
Thể tích viên bi sắt là:
\(V = \frac{4}{3}\pi {r^3} = \frac{4}{3}.3,14.2,{5^3} \approx 65\left( {c{m^3}} \right)\)
Khi đó thể tích nước và viên bi là:
\(352 + 65 = 417\left( {c{m^3}} \right)\)
Vì \(417c{m^3} < 603c{m^3}\) nên nước không tràn ra ngoài.
d) Sai
Bán kính viên bi sắt là: \(\frac{6}{2} = 3\left( {cm} \right)\)
Thể tích viên bi sắt là: \(V = \frac{4}{3}\pi {r^3} = \frac{4}{3}.3,{14.3^3} \approx 113\left( {c{m^3}} \right)\)
Khi đó thể tích nước và viên bi là: \(352 + 113 = 465\left( {c{m^3}} \right)\)
Vì \(465c{m^3} < 603c{m^3}\) nên nước không tràn ra ngoài.
Đáp án: SĐĐS
Phương trình \(\frac{{2x}}{{x - 2}} - \frac{5}{{x - 3}} = \frac{{ - 9}}{{{x^2} - 5x + 6}}\) \(\left( {x \ne 2;x \ne 3} \right)\) có bao nhiêu nghiệm?
Đáp án:
Đáp án:
Đưa phương trình về phương trình bậc hai một ẩn.
Tính \(\Delta \) để xác định số nghiệm.
Ta có: \(\frac{{2x}}{{x - 2}} - \frac{5}{{x - 3}} = \frac{{ - 9}}{{{x^2} - 5x + 6}}\)
\(\frac{{2x}}{{x - 2}} - \frac{5}{{x - 3}} = \frac{{ - 9}}{{\left( {x - 2} \right)\left( {x - 3} \right)}}\)
\(\frac{{2x\left( {x - 3} \right)}}{{\left( {x - 2} \right)\left( {x - 3} \right)}} - \frac{{5\left( {x - 2} \right)}}{{\left( {x - 2} \right)\left( {x - 3} \right)}} = \frac{{ - 9}}{{\left( {x - 2} \right)\left( {x - 3} \right)}}\)
\(2{x^2} - 6x - 5x + 10 + 9 = 0\)
\(2{x^2} - 11x + 19 = 0\)
Ta có: \(\Delta = {\left( { - 11} \right)^2} - 4.2.19 = - 31 < 0\) nên phương trình đã cho vô nghiệm.
Đáp án: 0
Khảo sát độ tuổi nhân viên của công ty S được chia ra làm 4 nhóm chính: từ 20 tuổi đến dưới 30 tuổi, từ 30 tuổi đến dưới 40 tuổi, từ 40 tuổi đến dưới 50 tuổi và từ 50 tuổi đến dưới 60 tuổi và kết quả được biểu diễn qua biểu đồ đoạn thẳng như hình vẽ dưới đây. Biết tổng số nhân viên có độ tuổi từ 20 đến dưới 40 tuổi là 430 người. Tính số nhân viên có độ tuổi từ 20 đến dưới 30 tuổi.
Đáp án:
Đáp án:
Xác định tần số tương đối tương ứng với số nhân viên có độ tuổi từ 20 đến dưới 40 tuổi.
Ta tính được tổng số nhân viên của công ty S.
Từ đó tính được số nhân viên có độ tuổi từ 20 đến dưới 30 tuổi.
Tần số tương đối của số nhân viên có độ tuổi từ 20 đến dưới 40 tuổi là:
\(25\% + 28,75\% = 53,75\% \).
Vì tổng số nhân viên có độ tuổi từ 20 đến dưới 40 tuổi là 430 người nên 430 ứng với \(53,75\% \).
Do đó số nhân viên của công ty S là: \(430:53,75\% = 800\) (người)
Vậy số nhân viên có độ tuổi từ 20 đến dưới 30 tuổi là: \(800.25\% = 200\) người.
Đáp án: 200
Một nhóm bạn có 4 bạn gồm 2 bạn nam là Hiếu, An và hai bạn nữ là Linh, Ngọc. Chọn ngẫu nhiên 2 bạn để tham gia lao động. Số phần tử của không gian mẫu bằng bao nhiêu?
Đáp án:
Đáp án:
Liệt kê các phần tử của không gian mẫu.
Không gian mẫu “Chọn ngẫu nhiên 2 bạn để tham gia lao động” là:
\(\Omega \) = {(Hiếu, An), (Hiếu, Linh), (Hiếu, Ngọc), (An, Linh), (An, Ngọc), (Linh, Ngọc)}
Vậy số phần tử của không gian mẫu là 6.
Đáp án: 6
Cạnh của một ngũ giác đều nội tiếp đường tròn bán kính \(4cm\) (làm tròn đến chữ số thập phân thứ nhất) là bao nhiêu cm?
Đáp án:
Đáp án:
Tính số đo mỗi góc ở tâm ứng với một cạnh: \(\frac{{360^\circ }}{n}\) (với n là số cạnh của đa giác) suy ra số đo \(\widehat {AOH}\).
Áp dụng tỉ số lượng giác vào tam giác \(\Delta AOH\) để tính AH, suy ra AB.
Giả sử ta có tam giác OAB như hình vẽ với O là tâm của ngũ giác đều.
Khi đó tam giác OAB cân tại O.
Kẻ \(OH \bot AB\), khi đó OH là đường cao đồng thời là đường trung tuyến và đường phân giác của tam giác OAB.
Do đó \(AH = \frac{1}{2}AB,\widehat {AOH} = \frac{1}{2}\widehat {AOB}\).
Ta có mỗi góc ở tâm ứng với mỗi cạnh của ngũ giác đều là:
\(\widehat {AOB} = \frac{{360^\circ }}{5} = 72^\circ \).
Suy ra \(\widehat {AOH} = \frac{1}{2}\widehat {AOB} = \frac{1}{2}.72^\circ = 36^\circ \) (cmt)
Xét \(\Delta AOH\) vuông tại \(H\) có: \(\sin AOH = \frac{{AH}}{{AO}}\)
Suy ra \(AH = AO.\sin AOH = 4.\sin 36^\circ \)
Do đó \(AB = 2AH = 2.4\sin 36^\circ \approx 4,7\) (cm)
Đáp án: 4,7
a) Thay toạ độ của điểm M vào hàm số để tìm a.
b) Dùng \(\Delta = {b^2} - 4ac\) để xác định số nghiệm của phương trình.
Tính tổng và tích của hai nghiệm \({x_1},{x_2}\) theo định lí Viète: \(\left\{ \begin{array}{l}S = {x_1} + {x_2} = \frac{{ - b}}{a}\\P = {x_1}{x_2} = \frac{c}{a}\end{array} \right.\).
Biến đổi biểu thức M để xuất hiện tổng và tích của hai nghiệm.
a) Để đồ thị hàm số \(y = a{x^2}\) đi qua \(M\left( {\sqrt 2 \,;{\rm{ }}2} \right)\) thì
\(2 = a.{(\sqrt 2 )^2}\)
\(2 = a.2\)
\(a = 1\)
Vậy với \(a = 1\) thì đồ thị hàm số \(y = a{x^2}\) đi qua \(M\left( {\sqrt 2 \,;{\rm{ }}2} \right).\)
b) Xét phương trình \({x^2} - 7x + 12 = 0\) có: \(\Delta = {\left( { - 7} \right)^2} - 4.12 = 49 - 48 = 1 > 0\) nên phương trình có hai nghiệm phân biệt \({x_1},{x_2}\).
Áp dụng định lí Viète, ta có:
\(\left\{ \begin{array}{l}S = {x_1} + {x_2} = \frac{{ - \left( { - 7} \right)}}{1} = 7\\P = {x_1}{x_2} = \frac{{12}}{1} = 12\end{array} \right.\)
Ta có:
\(\begin{array}{l}M = \left( {1 - 25{x_1}} \right){x_1} - {x_2}\left( {25{x_2} - {x_1} - 1} \right)\\ = {x_1} - 25x_1^2 - 25x_2^2 + {x_1}{x_2} + {x_2}\\ = - 25x_1^2 - 25x_2^2 - 50{x_1}{x_2} + 50{x_1}{x_2} + {x_1}{x_2} + {x_1} + {x_2}\\ = - 25\left( {{x_1}^2 + 2{x_1}{x_2} + x_2^2} \right) + 51{x_1}{x_2} + \left( {{x_1} + {x_2}} \right)\\ = - 25{\left( {{x_1} + {x_2}} \right)^2} + 51{x_1}{x_2} + \left( {{x_1} + {x_2}} \right)\\ = - {25.7^2} + 51.12 + 7\\ = - 606\end{array}\)
Vậy \(M = - 606\)
a) Chứng minh \(\Delta CAO\) và \(\Delta CMO\) cùng thuộc đường tròn đường kính CO.
Do đó A, C, M, O cùng thuộc đường tròn đường kính CO hay tứ giác ACMO nội tiếp đường tròn đường kính CO.
b) Chứng minh \(\widehat {CAM} = \widehat {ABM}\)
Chứng minh tứ giác DMOB nội tiếp nên \(\widehat {ABM} = \widehat {ODM}\).
Suy ra \(\widehat {CAM} = \widehat {ODM}\).
c) Chứng minh PA.PO = PC.PM
Chứng minh $\Delta PAC\backsim \Delta PMO$ (g.g) suy ra PA.PO = PC.PM.
Chứng minh E, F, P thẳng hàng
Chứng minh $\Delta PAF\backsim \Delta PBE$ suy ra \(\widehat {PFA} = \widehat {PEB}\)
Chứng minh ABEF là hình thang vuông nên \(\widehat {AFE} + \widehat {BEF} = 180^\circ \)
Suy ra \(\widehat {PFA} + \widehat {AFE} = 180^\circ \) hay \(\widehat {PFE} = 180^\circ \) nên E, F, P thẳng hàng.
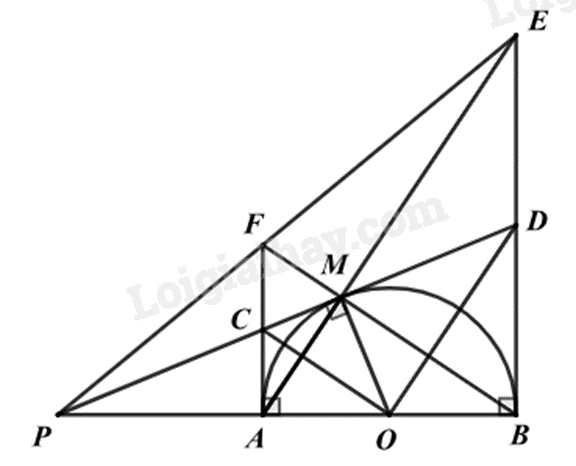
a) Vì AC và MC là hai tiếp tuyến của đường tròn (O) nên \(\widehat {CAO} = 90^\circ ,\widehat {CMO} = 90^\circ \).
Xét \(\Delta CAO\) vuông tại A \(\left( {\widehat {CAO} = 90^\circ } \right)\) nên \(\Delta CAO\) nội tiếp đường tròn đường kính CO, suy ra C, A, O thuộc đường tròn đường kính CO.
Xét \(\Delta CMO\) vuông tại M \(\left( {\widehat {CMO} = 90^\circ } \right)\) nên \(\Delta CMO\) nội tiếp đường tròn đường kính CO, suy ra C, M, O thuộc đường tròn đường kính CO.
Do đó A, C, M, O cùng thuộc đường tròn đường kính CO hay tứ giác ACMO nội tiếp đường tròn đường kính CO.
b) Ta có: \(\widehat {CAM} + \widehat {MAB} = \widehat {CAB} = 90^\circ \) (1)
Vì \(\widehat {AMB} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn) nên \(\Delta AMB\) vuông tại M, suy ra \(\widehat {MAB} + \widehat {ABM} = 90^\circ \) (2)
Từ (1) và (2) suy ra \(\widehat {CAM} = \widehat {ABM}\) (3)
Xét \(\Delta DMO\) vuông tại M \(\left( {\widehat {DMO} = 90^\circ } \right)\) nên D, M, O thuộc đường tròn đường kính OD.
Xét \(\Delta DBO\) vuông tại B \(\left( {\widehat {DBO} = 90^\circ } \right)\) nên D, B, O thuộc đường tròn đường kính OD.
Do đó D, M, O, B cùng thuộc đường tròn đường kính OD hay tứ giác DMOB nội tiếp đường tròn đường kính OD.
Do đó \(\widehat {ABM} = \widehat {ODM}\) (hai góc nội tiếp cùng chắn cung OM) (4)
Từ (3) và (4) suy ra \(\widehat {CAM} = \widehat {ODM}\).
c) Chứng minh PA.PO = PC.PM
Xét \(\Delta PAC\) và \(\Delta PMO\) có:
\(\widehat P\) chung
\(\widehat {PAC} = \widehat {PMO}\left( { = 90^\circ } \right)\)
suy ra $\Delta PAC\backsim \Delta PMO$ (g.g)
Suy ra \(\frac{{PA}}{{PC}} = \frac{{PM}}{{PO}}\) (tỉ lệ các cặp cạnh tương ứng)
Suy ra PA.PO = PC.PM.
Chứng minh E, F, P thẳng hàng
Vì \(AF \bot AB,BE \bot AB\) (hai tiếp tuyến của đường tròn) suy ra \(AF//BE\).
suy ra $\Delta PAF\backsim \Delta PBE$ (định lí hai tam giác đồng dạng)
suy ra \(\widehat {PFA} = \widehat {PEB}\) (hai góc tương ứng) (5)
Tứ giác ABEF có AF // BE nên là hình thang.
Mà \(\widehat A = \widehat B = 90^\circ \) nên ABEF là hình thang vuông.
Suy ra \(\widehat {AFE} + \widehat {BEF} = 360^\circ - 90^\circ - 90^\circ = 180^\circ \) (6)
Từ (5) và (6) suy ra \(\widehat {PFA} + \widehat {AFE} = 180^\circ \) hay \(\widehat {PFE} = 180^\circ \) nên E, F, P thẳng hàng.
Sử dụng công thức tính thể tích hình trụ để tính bán kính đáy: \({V_T} = \pi {r^2}h\).
Sử dụng công thức tính thể tích hình cầu để tính lượng nước bị tràn ra ngoài (vì thể tích viên bi bằng thể tích nước bị tràn ra ngoài): \({V_C} = \frac{4}{3}\pi {r^3}\).
Ta có thể tích của cốc thuỷ tinh là: \({V_T} = \pi {r^2}h\) hay \(90\pi = \pi {r^2}.10\)
suy ra \({r^2} = \frac{{90\pi }}{{10\pi }} = 9\) nên \(r = \sqrt 9 = 3\left( {cm} \right)\)
Vì bán kính viên bi sắt bằng bán kính đáy cốc nên thể tích viên bi sắt là: \({V_C} = \frac{4}{3}\pi {r^3} \approx \frac{4}{3}.3,{14.3^3} = 113,04\left( {c{m^3}} \right)\)
Vì thể tích viên bi sắt bằng lượng nước bị tràn ra ngoài nên lượng nước bị tràn ra ngoài khoảng \(113,04c{m^3}\).
