Đề khảo sát chất lượng đầu năm Toán 9 THCS Thuận Thành – Bắc Ninh

Đề bài

I. PHẦN TRẮC NGHIỆM (4,0 điểm):

Chọn câu trả lời đúng và ghi vào bài làm

Câu 1. Phương trình \(3x - 7 =  - x + 1\) có nghiệm là:

A. \(x = 3\)

B. \(x = 2\)

C. \(x = \frac{2}{3}\)

D. \(x = \frac{3}{2}\)

Câu 2. Cho biết đồ thị của hàm số \(y = 1 - 2x\) và đồ thị của hàm số \(y = ax + 3\) là hai đường thẳng song song, khi đó hệ số a bằng:

A. 1

B. 3

C. 2

D. \( - 2\)

Câu 3. Điều kiện xác định của phương trình \(\frac{{x - 1}}{{x + 3}} = \frac{{x - 2}}{{x - 5}}\) là:

A. \(x \ne 5\)

B. \(x \ne  - 3\)

C. \(x \ne 5;x \ne  - 3\)

D. \(x \ne  - 3;x \ne  - 5\)

Câu 4. Kết quả của phân tích đa thức \(25 - {(x - 2)^2}\) thành nhân tử là:

A. \((3 + x)(7 - x)\)

B. \(5(x - 2)\)

C. \((7 + x)(x + 3)\)

D. \((3 - x)(7 + x)\)

Câu 5. Cho \(\Delta ABC\) có \(\hat A = 60^\circ \), \(AB = 2\)cm, \(AC = 3\)cm; \(\Delta MNQ\) có \(\hat N = 60^\circ \), \(NM = 6\)cm, \(NQ = 4\)cm. Cách viết nào dưới đây đúng?

A. $\Delta ABC \backsim \Delta MNQ$

B. $\Delta ABC \backsim \Delta NMQ$

C. $\Delta BAC\backsim \Delta QNM$

D. $\Delta BAC\backsim \Delta MNQ$

Câu 6. Giá trị của x trong hình vẽ sau là:

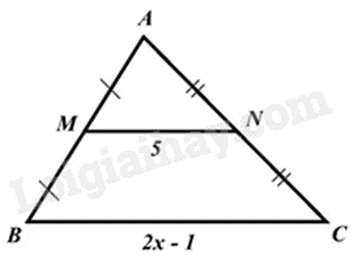
A. 10.

B. 5,5.

C. 3.

D. 1,75

Câu 7. Trong hộp có 12 viên bi gồm 3 viên bi màu xanh, 4 viên bi màu đỏ, 5 viên bi màu vàng. Các viên bi có hình dạng và kích thước giống hệt nhau. Chọn ngẫu nhiên một viên bi. Xác suất của biến cố “Viên bi được chọn có màu đỏ” bằng.

A. \(\frac{1}{3}\)

B. \(\frac{1}{{12}}\)

C. \(\frac{1}{4}\)

D. 4

Câu 8. Để đường thẳng \(y = 3 - ax\) đi qua điểm \(A( - 1;5)\) thì a bằng:
A. 2

B. 3

C. \( - 3\)

D. \( - 2\)

II. PHẦN TỰ LUẬN (6,0 điểm)

Câu 9 (2,0 điểm)

a) Giải phương trình: \(5x + 14 = 63 - 2x\)

b) Tìm m biết đường thẳng \(y = (m - 2)x + 5\) với \((m \ne 2)\) đi qua điểm \(A( - 1;4)\).

c) Rút gọn biểu thức: \(A = \frac{{3 + x}}{{x - 3}} + \frac{{36}}{{(x - 3)(x + 3)}} - \frac{{x - 3}}{{x + 3}}\) (với \(x \ne 3\); \(x \ne  - 3\))

Câu 10 (1,0 điểm) Giải bài toán sau bằng cách lập phương trình

Hai ô tô cùng khởi hành một lúc từ A đến B. Ô tô thứ nhất đi với vận tốc 40 km/h, ô tô thứ hai đi với vận tốc 50 km/h. Biết rằng ô tô thứ nhất tới B chậm hơn ô tô thứ hai là 1 giờ 30 phút. Tính quãng đường AB.

Câu 11 (2,5 điểm)

Cho tam giác ABC vuông tại A, đường cao AH (H thuộc BC)

a) Chứng minh \(\Delta ABH\) và \(\Delta CBA\) đồng dạng.

b) Gọi N, M lần lượt là trung điểm của AB và BC, từ B kẻ đường thẳng vuông góc với BC cắt tia MN tại I. Chứng minh rằng: \(MN//AC\) và \(B{I^2} = MI \cdot NI\)

c) Gọi O là giao điểm của AH và IC. Chứng minh O là trung điểm của AH.

Câu 12 (0,5 điểm). Giải phương trình

\({(2024 - x)^3} + {(2026 - x)^3} + {(2x - 4050)^3} = 0\)

----HẾT----

Lời giải chi tiết

I. PHẦN TRẮC NGHIỆM (4,0 điểm):

Câu 1. Phương trình \(3x - 7 =  - x + 1\) có nghiệm là:

A. \(x = 3\)

B. \(x = 2\)

C. \(x = \frac{2}{3}\)

D. \(x = \frac{3}{2}\)

Phương pháp:

Giải phương trình bậc nhất một ẩn.

Cách giải:

$3x-7=-x+1 \\3x+x=1+7 \\4x=8 \\x=2$

Đáp án: B

Câu 2. Cho biết đồ thị của hàm số \(y = 1 - 2x\) và đồ thị của hàm số \(y = ax + 3\) là hai đường thẳng song song, khi đó hệ số a bằng:

A. 1

B. 3

C. 2

D. \( - 2\)

Phương pháp:

Đồ thị của hàm số \(y = ax + b\left( {a \ne 0} \right)\) và \(y = a'x + b'\left( {a' \ne 0} \right)\) là hai đường thẳng song song nếu \(a = a',b \ne b'\)

Cách giải:

Đồ thị của hàm số \(y = 1 - 2x\) và đồ thị của hàm số \(y = ax + 3\) là hai đường thẳng song song thì \(a =  - 2\).

Đáp án: D

Câu 3. Điều kiện xác định của phương trình \(\frac{{x - 1}}{{x + 3}} = \frac{{x - 2}}{{x - 5}}\) là:

A. \(x \ne 5\)

B. \(x \ne  - 3\)

C. \(x \ne 5;x \ne  - 3\)

D. \(x \ne  - 3;x \ne  - 5\)

Phương pháp:

Điều kiện xác định của phân thức đại số là mẫu thức khác 0.

Cách giải:

\(\frac{{x - 1}}{{x + 3}} = \frac{{x - 2}}{{x - 5}}\) xác định khi \(x + 3 \ne 0\) và \(x - 5 \ne 0\)

Suy ra \(x \ne  - 3\) và \(x \ne 5\).

Đáp án: C

Câu 4. Kết quả của phân tích đa thức \(25 - {(x - 2)^2}\) thành nhân tử là:

A. \((3 + x)(7 - x)\)

B. \(5(x - 2)\)

C. \((7 + x)(x + 3)\)

D. \((3 - x)(7 + x)\)

Phương pháp:

Sử dụng hằng đẳng thức \({a^2} - {b^2} = \left( {a - b} \right)\left( {a + b} \right)\) để phân tích đa thức thành nhân tử.

Cách giải:

\(\begin{array}{l}25 - {(x - 2)^2}\\ = {5^2} - {\left( {x - 2} \right)^2}\\ = \left( {5 - x + 2} \right)\left( {5 + x - 2} \right)\\ = \left( {7 - x} \right)\left( {3 + x} \right)\end{array}\)

Đáp án: A

Câu 5. Cho \(\Delta ABC\) có \(\hat A = 60^\circ \), \(AB = 2\)cm, \(AC = 3\)cm; \(\Delta MNQ\) có \(\hat N = 60^\circ \), \(NM = 6\)cm, \(NQ = 4\)cm. Cách viết nào dưới đây đúng?

A. $\Delta ABC \backsim \Delta MNQ$

B. $\Delta ABC \backsim \Delta NMQ$

C. $\Delta BAC\backsim \Delta QNM$

D. $\Delta BAC\backsim \Delta MNQ$

Phương pháp:

Chứng minh hai tam giác đồng dạng theo trường hợp cạnh – góc – cạnh và để xác định các đỉnh tương ứng.

Cách giải:

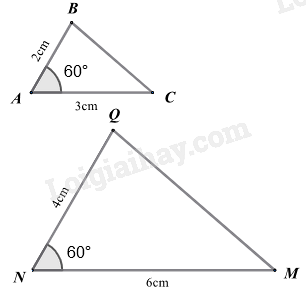
Xét \(\Delta ABC\) và \(\Delta MNQ\) có:

\(\widehat A = \widehat N\)

\(\frac{{AB}}{{NQ}} = \frac{{AC}}{{NM}}\left( {\frac{2}{4} = \frac{3}{6}} \right)\)

nên $\Delta BAC\backsim \Delta QNM\left( c.g.c \right)$

Đáp án: C

Câu 6. Giá trị của x trong hình vẽ sau là:

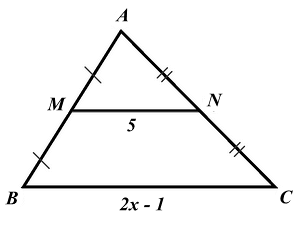
A. 10.

B. 5,5.

C. 3.

D. 1,75

Phương pháp:

Sử dụng kiến thức về đường trung bình.

Cách giải:

Vì AM = MB, AN = NC nên M, N lần lượt là trung điểm của AB và AC, do đó MN là đường trung bình của tam giác ABC.

Suy ra

\(\begin{array}{l}MN = \frac{1}{2}BC\\5 = \frac{1}{2}.\left( {2x - 1} \right)\\2x - 1 = 10\\2x = 11\\x = \frac{{11}}{2} = 5,5\end{array}\)

Đáp án: B

Câu 7. Trong hộp có 12 viên bi gồm 3 viên bi màu xanh, 4 viên bi màu đỏ, 5 viên bi màu vàng. Các viên bi có hình dạng và kích thước giống hệt nhau. Chọn ngẫu nhiên một viên bi. Xác suất của biến cố “Viên bi được chọn có màu đỏ” bằng.

A. \(\frac{1}{3}\)

B. \(\frac{1}{{12}}\)

C. \(\frac{1}{4}\)

D. 4

Phương pháp:

Xác định số kết quả có thể, số kết quả thuận lợi.

Xác suất của biến cố bằng tỉ số giữa số kết quả thuận lợi và số kết quả có thể.

Cách giải:

Vì có 12 viên bi nên có 12 kết quả có thể khi chọn ngẫu nhiên một viên bi.

Có 4 viên bi màu đỏ nên có 4 kết quả thuận lợi cho biến cố “Viên bi được chọn có màu đỏ”.

Xác suất của biến cố là: \(\frac{4}{{12}} = \frac{1}{3}\).

Đáp án: A

Câu 8. Để đường thẳng \(y = 3 - ax\) đi qua điểm \(A( - 1;5)\) thì a bằng:
A. 2

B. 3

C. \( - 3\)

D. \( - 2\)

Phương pháp:

Thay toạ độ điểm A vào hàm số để tìm a.

Cách giải:

Vì đường thẳng đi qua A nên thay \(x =  - 1;y = 5\) vào hàm số, ta được:

\(\begin{array}{l}5 = 3 - a.\left( { - 1} \right)\\5 = 3 + a\\a = 5 - 3\\a = 2\end{array}\)

Đáp án: A

II. PHẦN TỰ LUẬN (6,0 điểm)

Câu 9 (2,0 điểm)

a) Giải phương trình: \(5x + 14 = 63 - 2x\)

b) Tìm m biết đường thẳng \(y = (m - 2)x + 5\) với \((m \ne 2)\) đi qua điểm \(A( - 1;4)\).

c) Rút gọn biểu thức: \(A = \frac{{3 + x}}{{x - 3}} + \frac{{36}}{{(x - 3)(x + 3)}} - \frac{{x - 3}}{{x + 3}}\) (với \(x \ne 3\); \(x \ne  - 3\))

Phương pháp:

a) Giải phương trình bậc nhất một ẩn.

b) Thay toạ độ điểm A vào hàm số để tìm m.

c) Quy đồng mẫu để cộng, trừ phân thức khác mẫu.

Cách giải:

a) \(5x + 14 = 63 - 2x\)

\(\begin{array}{l}5x + 2x = 63 - 14\\7x = 49\\x = 7\end{array}\)

Vậy nghiệm của phương trình là \(x = 7\).

b) Vì đường thẳng \(y = (m - 2)x + 5\) đi qua điểm A nên thay \(x =  - 1;y = 4\) vào hàm số, ta được:

\(\begin{array}{l}4 = (m - 2).\left( { - 1} \right) + 5\\4 =  - m + 2 + 5\\m = 2 + 5 - 4\\m = 3\end{array}\)

Vậy \(m = 3\).

c) \(A = \frac{{3 + x}}{{x - 3}} + \frac{{36}}{{(x - 3)(x + 3)}} - \frac{{x - 3}}{{x + 3}}\)

\(\begin{array}{l} = \frac{{{{\left( {3 + x} \right)}^2}}}{{(x - 3)(x + 3)}} + \frac{{36}}{{(x - 3)(x + 3)}} - \frac{{{{\left( {x - 3} \right)}^2}}}{{(x - 3)(x + 3)}}\\ = \frac{{9 + 6x + {x^2}}}{{(x - 3)(x + 3)}} + \frac{{36}}{{(x - 3)(x + 3)}} - \frac{{{x^2} - 6x + 9}}{{(x - 3)(x + 3)}}\\ = \frac{{9 + 6x + {x^2} + 36 - {x^2} + 6x - 9}}{{(x - 3)(x + 3)}}\\ = \frac{{12x + 36}}{{(x - 3)(x + 3)}}\\ = \frac{{12\left( {x + 3} \right)}}{{(x - 3)(x + 3)}}\\ = \frac{{12}}{{x - 3}}\end{array}\)

Câu 10 (1,0 điểm) Giải bài toán sau bằng cách lập phương trình

Hai ô tô cùng khởi hành một lúc từ A đến B. Ô tô thứ nhất đi với vận tốc 40 km/h, ô tô thứ hai đi với vận tốc 50 km/h. Biết rằng ô tô thứ nhất tới B chậm hơn ô tô thứ hai là 1 giờ 30 phút. Tính quãng đường AB.

Phương pháp:

Gọi độ dài quãng đường AB là \(x\) (km), \(x > 0\).

Biểu diễn thời gian ô tô thứ nhất và ô tô thứ hai đi quãng đường AB.

Vì ô tô thứ nhất tới B chậm hơn ô tô thứ hai là 1 giờ 30 phút nên ta lập được phương trình.

Giải phương trình để tìm \(x\).

Cách giải:

Gọi độ dài quãng đường AB là \(x\) (km), \(x > 0\).

Thời gian ô tô thứ nhất đi quãng đường AB là: \(\frac{x}{{40}}\) (h)

Thời gian ô tô thứ hai đi quãng đường AB là: \(\frac{x}{{50}}\) (h)

Vì ô tô thứ nhất tới B chậm hơn ô tô thứ hai là 1 giờ 30 phút = 1,5h nên ta có phương trình:

\(\begin{array}{l}\frac{x}{{40}} - \frac{x}{{50}} = 1,5\\5x - 4x = 1,5.200\\x = 300\left( {TM} \right)\end{array}\)

Vậy độ dài quãng đường AB là 300 km.

Câu 11 (2,5 điểm)

Cho tam giác ABC vuông tại A, đường cao AH (H thuộc BC)

a) Chứng minh \(\Delta ABH\) và \(\Delta CBA\) đồng dạng.

b) Gọi N, M lần lượt là trung điểm của AB và BC, từ B kẻ đường thẳng vuông góc với BC cắt tia MN tại I. Chứng minh rằng: \(MN//AC\) và \(B{I^2} = MI \cdot NI\)

c) Gọi O là giao điểm của AH và IC. Chứng minh O là trung điểm của AH.

Phương pháp:

a) Chứng minh $\Delta ABH\backsim \Delta CBA$ (g.g)

b) Chứng minh $\Delta BIN\backsim \Delta MIB$ (g.g) nên \(B{I^2} = MI \cdot NI\).

c) Gọi D là giao điểm của BI và AC

Chứng minh BI = ID bằng định lí đường trung bình.

Sử dụng định lí hai tam giác bằng nhau để chứng minh \(\frac{{OH}}{{BI}} = \frac{{CO}}{{CI}}\) và \(\frac{{AO}}{{ID}} = \frac{{CO}}{{CI}}\)

Do đó \(OH = AO\) hay O là trung điểm của AH.

Cách giải:

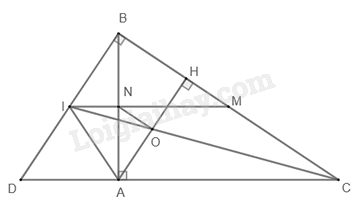
a) Xét \(\Delta ABH\) và \(\Delta CBA\) có:

\(\widehat {AHB} = \widehat {CAB}\left( { = 90^\circ } \right)\)

\(\widehat {ABC}\) chung

Vậy $\Delta ABH\backsim \Delta CBA$ (g.g)

b) Vì N, M lần lượt là trung điểm của AB và BC nên NM là đường trung bình của \(\Delta ABC\), do đó MN // AC.

Vì MN // AC và \(AB \bot AC\) (tam giác ABC vuông tại A) nên \(MN \bot AB\).

Xét \(\Delta BIN\) và \(\Delta MIB\) có:

\(\widehat {BNI} = \widehat {MBI}\)

\(\widehat {BIM}\) chung

Do đó $\Delta BIN\backsim \Delta MIB$ (g.g)

Suy ra \(\frac{{BI}}{{IN}} = \frac{{IM}}{{BI}}\), hay \(B{I^2} = MI \cdot NI\).

c) Gọi D là giao điểm của BI và AC

Vì MN // AC nên IM // CD (do I thuộc tia MN, D thuộc đường thẳng AC).

Mà M là trung điểm của BC nên I là trung điểm của BD hay BI = ID (1).

Xét \(\Delta COH\) và \(\Delta CIB\) có OH // BI (do AH và BI cùng vuông góc với BC) nên $\Delta COH\backsim \Delta CIB$ (định lí)

Do đó \(\frac{{OH}}{{BI}} = \frac{{CO}}{{CI}}\) (2)

Xét \(\Delta COA\) và \(\Delta CID\) có OA // ID (do AH và BI cùng vuông góc với BC) nên $\Delta COA=\Delta CID$ (định lí)

Do đó \(\frac{{AO}}{{ID}} = \frac{{CO}}{{CI}}\) (3)

Từ (1), (2) và (3) suy ra \(OH = AO\) hay O là trung điểm của AH.

Câu 12 (0,5 điểm) Giải phương trình

\({(2024 - x)^3} + {(2026 - x)^3} + {(2x - 4050)^3} = 0\)

Phương pháp:

Đặt \(t = 2025 - x\).

Sử dụng hằng đẳng thức lập phương của một tổng, một hiệu để rút gọn biểu thức bên trái.

Từ đó giải phương trình để tìm \(t\).

Ta tính được các giá trị \(x\) tương ứng.

Cách giải:

Đặt \(t = 2025 - x\).

Khi đó, phương trình trở thành: \({\left( {t - 1} \right)^3} + {\left( {t + 1} \right)^3} + {\left( { - 2t} \right)^3} = 0\)

\(\begin{array}{l}{\left( {t - 1} \right)^3} + {\left( {t + 1} \right)^3} + {\left( { - 2t} \right)^3} = 0\\{t^3} - 3{t^2} + 3t - 1 + {t^3} + 3{t^2} + 3t + 1 - 8{t^3} = 0\\ - 6{t^3} + 6t = 0\\ - 6t\left( {{t^2} - 1} \right) = 0\\ - 6t\left( {t - 1} \right)\left( {t + 1} \right) = 0\end{array}\)

Do đó \(t = 0;t = 1;t =  - 1\).

Với \(t = 1\) thì \(2025 - x = 1\) suy ra \(x = 2024\).

Với \(t = 0\) thì \(2025 - x = 0\) suy ra \(x = 2025\).

Với \(t =  - 1\) thì \(2025 - x =  - 1\) suy ra \(x = 2026\).

Vậy phương trình có nghiệm là \(x \in \left\{ {2024;2025;2026} \right\}\).