Đề thi học kì 1 Toán 9 - Đề số 2
Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau:
Đề bài
Cặp số \(\left( {4;2} \right)\) là nghiệm của hệ phương trình
-
A.
\(\left\{ \begin{array}{l}x + y = 6\\x - y = 2\end{array} \right.\).
-
B.
\(\left\{ \begin{array}{l}x - y = 2\\3x + 2y = 5\end{array} \right.\).
-
C.
\(\left\{ \begin{array}{l}x + y = 6\\2x - 5y = 8\end{array} \right.\).
-
D.
\(\left\{ \begin{array}{l}x - y = 2\\x - 5y = 4\end{array} \right.\).
Bất đẳng thức \(a + 1 < 3\) có vế trái là:
-
A.
\(a + 1\).
-
B.
\(a\).
-
C.
\(1\).
-
D.
\(3\).
So sánh hai số 2 và \(1 + \sqrt 2 \)
-
A.
Không thể so sánh.
-
B.
\(2 = 1 + \sqrt 2 \).
-
C.
\(2 > 1 + \sqrt 2 \).
-
D.
\(2 < 1 + \sqrt 2 \).
Điều kiện xác định của biểu thức \(\sqrt {x - 10} \) là:
-
A.
\(x - 10 < 0\).
-
B.
\(x - 10 \le 0\).
-
C.
\(x \ge 10\).
-
D.
\(x \le 10\).
Biểu thức \(\sqrt {{{\left( {3 - 2x} \right)}^2}} \) bằng
-
A.
\(3 - 2x\).
-
B.
\(2x - 3\).
-
C.
\(\left| {2x - 3} \right|\).
-
D.
\(3x - 2\) và \(2 - 3x\).
Trục căn thức biểu thức \(\sqrt {\frac{2}{{5{a^3}}}} \) với \(a > 0\) được
-
A.
\(\frac{{\sqrt {10a} }}{{5{a^2}}}\).
-
B.
\(\frac{{\sqrt {10a} }}{{5{a^3}}}\).
-
C.
\(\frac{{\sqrt 2 }}{{5{a^2}}}\).
-
D.
\(\frac{2}{{5{a^2}}}\).
Rút gọn biểu thức \(\sqrt[3]{{27{x^3}}} - \sqrt[3]{{8{x^3}}} + 4x\) ta được
-
A.
\(23\sqrt[3]{x}\).
-
B.
\(23x\).
-
C.
\(15x\).
-
D.
\(5x\).
Chọn đáp án đúng:
-
A.
\(\cot 37^\circ = \cot 53^\circ \).
-
B.
\(\cos 37^\circ = \sin 53^\circ \).
-
C.
\(\tan 37^\circ = \cos 37^\circ \).
-
D.
\(\sin 37^\circ = \sin 53^\circ \).
Cung cả đường tròn có số đo
-
A.
\(360^\circ \).
-
B.
\(270^\circ \).
-
C.
\(180^\circ \).
-
D.
\(90^\circ \).
-
A.
\(110^\circ \).
-
B.
\(220^\circ \).
-
C.
\(140^\circ \).
-
D.
\(250^\circ \).
Một hình quạt tròn có bán kính 6cm, số đo cung là \(36^\circ \). Diện tích hình quạt tròn đó là
-
A.
\(3,6\pi \left( {cm} \right)\).
-
B.
\(3,6\pi \left( {c{m^2}} \right)\).
-
C.
\(7,2\pi \left( {c{m^2}} \right)\).
-
D.
\(6\pi \left( {c{m^2}} \right)\).
Hai tiếp tuyến tại B và C của đường tròn (O) cắt nhau tại A. Chọn khẳng định sai.
-
A.
\(AB = AC\).
-
B.
\(OA \bot BC\).
-
C.
\(OA\) là đường trung trực của BC.
-
D.
\(OA \bot BC\) tại trung điểm của OA.
Lời giải và đáp án
Cặp số \(\left( {4;2} \right)\) là nghiệm của hệ phương trình
-
A.
\(\left\{ \begin{array}{l}x + y = 6\\x - y = 2\end{array} \right.\).
-
B.
\(\left\{ \begin{array}{l}x - y = 2\\3x + 2y = 5\end{array} \right.\).
-
C.
\(\left\{ \begin{array}{l}x + y = 6\\2x - 5y = 8\end{array} \right.\).
-
D.
\(\left\{ \begin{array}{l}x - y = 2\\x - 5y = 4\end{array} \right.\).
Đáp án : A
Thay \(\left( {4;2} \right)\) vào các hệ phương trình xem hệ nào thỏa mãn.
Vì \(\left\{ \begin{array}{l}4 + 2 = 6\\4 - 2 = 2\end{array} \right.\) nên cặp số \(\left( {4;2} \right)\) là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}x + y = 6\\x - y = 2\end{array} \right.\).
Đáp án A.
Bất đẳng thức \(a + 1 < 3\) có vế trái là:
-
A.
\(a + 1\).
-
B.
\(a\).
-
C.
\(1\).
-
D.
\(3\).
Đáp án : A
Hệ thức a < b là bất đẳng thức và a là vế trái, b là vế phải của bất đẳng thức.
Vế trái của bất đẳng thức là \(a + 1\).
Đáp án A.
So sánh hai số 2 và \(1 + \sqrt 2 \)
-
A.
Không thể so sánh.
-
B.
\(2 = 1 + \sqrt 2 \).
-
C.
\(2 > 1 + \sqrt 2 \).
-
D.
\(2 < 1 + \sqrt 2 \).
Đáp án : D
Sử dụng tính chất của bất đẳng thức để so sánh.
Vì \(1 < 2\) nên \(1 < \sqrt 2 \) suy ra \(1 + 1 < 1 + \sqrt 2 \) hay \(2 < 1 + \sqrt 2 \).
Đáp án D.
Điều kiện xác định của biểu thức \(\sqrt {x - 10} \) là:
-
A.
\(x - 10 < 0\).
-
B.
\(x - 10 \le 0\).
-
C.
\(x \ge 10\).
-
D.
\(x \le 10\).
Đáp án : C
Điều kiện xác định của \(\sqrt A \) là \(A \ge 0\).
Điều kiện xác định của biểu thức \(\sqrt {x - 10} \) là \(x - 10 \ge 0\) hay \(x \ge 10\).
Đáp án C.
Biểu thức \(\sqrt {{{\left( {3 - 2x} \right)}^2}} \) bằng
-
A.
\(3 - 2x\).
-
B.
\(2x - 3\).
-
C.
\(\left| {2x - 3} \right|\).
-
D.
\(3x - 2\) và \(2 - 3x\).
Đáp án : C
Sử dụng công thức \(\sqrt {{A^2}} = \left| A \right|\).
\(\sqrt {{{\left( {3 - 2x} \right)}^2}} = \left| {3 - 2x} \right| = \left| {2x - 3} \right|\).
Đáp án C.
Trục căn thức biểu thức \(\sqrt {\frac{2}{{5{a^3}}}} \) với \(a > 0\) được
-
A.
\(\frac{{\sqrt {10a} }}{{5{a^2}}}\).
-
B.
\(\frac{{\sqrt {10a} }}{{5{a^3}}}\).
-
C.
\(\frac{{\sqrt 2 }}{{5{a^2}}}\).
-
D.
\(\frac{2}{{5{a^2}}}\).
Đáp án : A
Với những căn thức bậc hai mà biểu thức dưới dấu căn có mẫu, ta thường khử mẫu của biểu thức lấy căn (biến đổi căn thức bậc hai đó thành một biểu thức mà trong căn thức không còn mẫu).
\(\sqrt {\frac{2}{{5{a^3}}}} = \sqrt {\frac{{2.5a}}{{25{a^4}}}} = \sqrt {\frac{{10a}}{{{{\left( {5{a^2}} \right)}^2}}}} = \frac{{\sqrt {10a} }}{{5{a^2}}}\).
Đáp án A.
Rút gọn biểu thức \(\sqrt[3]{{27{x^3}}} - \sqrt[3]{{8{x^3}}} + 4x\) ta được
-
A.
\(23\sqrt[3]{x}\).
-
B.
\(23x\).
-
C.
\(15x\).
-
D.
\(5x\).
Đáp án : D
Sử dụng kiến thức về căn thức bậc ba để rút gọn.
\(\begin{array}{l}\sqrt[3]{{27{x^3}}} - \sqrt[3]{{8{x^3}}} + 4x\\ = \sqrt[3]{{{{\left( {3x} \right)}^3}}} - \sqrt[3]{{{{\left( {2x} \right)}^3}}} + 4x\\ = 3x - 2x + 4x = 5x.\end{array}\)
Đáp án D.
Chọn đáp án đúng:
-
A.
\(\cot 37^\circ = \cot 53^\circ \).
-
B.
\(\cos 37^\circ = \sin 53^\circ \).
-
C.
\(\tan 37^\circ = \cos 37^\circ \).
-
D.
\(\sin 37^\circ = \sin 53^\circ \).
Đáp án : B
Sử dụng kiến thức về tỉ số lượng giác của hai góc phụ nhau.
Vì \(37^\circ \) và \(53^\circ \) là hai góc phụ nhau nên \(\sin 37^\circ = \cos 53^\circ ;\) \(\cos 37^\circ = \sin 53^\circ ;\) \(\tan 37^\circ = \cot 53^\circ ;\) \(\tan 53^\circ = \cot 37^\circ \).
Đáp án B.
Cung cả đường tròn có số đo
-
A.
\(360^\circ \).
-
B.
\(270^\circ \).
-
C.
\(180^\circ \).
-
D.
\(90^\circ \).
Đáp án : A
Sử dụng kiến thức về số đo cung.
Cung cả đường tròn có số đo là \(360^\circ \).
Đáp án A.
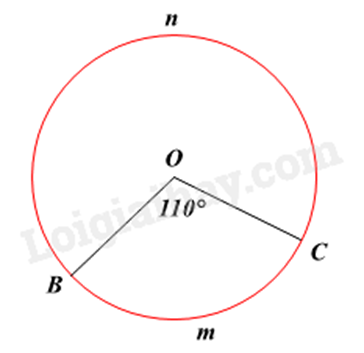
-
A.
\(110^\circ \).
-
B.
\(220^\circ \).
-
C.
\(140^\circ \).
-
D.
\(250^\circ \).
Đáp án : D
Góc \(BOC\) chính là góc ở tâm nên ta suy ra số đo cung nhỏ $\overset\frown{BmC}$.
Số đo cung lớn $\overset\frown{BnC}$ bằng hiệu giữa \(360^\circ \) và số đo của cung nhỏ có chung hai mút.
Vì góc BOC là góc ở tâm nên sđ$\overset\frown{BmC}=\widehat{BOC}=110{}^\circ $.
Số đo cung lớn $\overset\frown{BnC}$ là:
\(360^\circ - 110^\circ = 250^\circ \).
Đáp án D.
Một hình quạt tròn có bán kính 6cm, số đo cung là \(36^\circ \). Diện tích hình quạt tròn đó là
-
A.
\(3,6\pi \left( {cm} \right)\).
-
B.
\(3,6\pi \left( {c{m^2}} \right)\).
-
C.
\(7,2\pi \left( {c{m^2}} \right)\).
-
D.
\(6\pi \left( {c{m^2}} \right)\).
Đáp án : B
Sử dụng công thức tính diện tích hình quạt tròn: \({S_q} = \frac{{\pi {R^2}n}}{{360}}\).
Diện tích hình quạt tròn đó là: \({S_q} = \frac{{\pi {{.6}^2}.36}}{{360}} = 3,6\pi \left( {c{m^2}} \right)\)
Đáp án B.
Hai tiếp tuyến tại B và C của đường tròn (O) cắt nhau tại A. Chọn khẳng định sai.
-
A.
\(AB = AC\).
-
B.
\(OA \bot BC\).
-
C.
\(OA\) là đường trung trực của BC.
-
D.
\(OA \bot BC\) tại trung điểm của OA.
Đáp án : D
Sử dụng tính chất của hai tiếp tuyến cắt nhau.
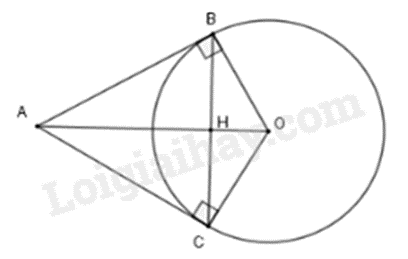
Vì hai tiếp tuyến tại B và C của đường tròn (O) cắt nhau tại A nên AB = AC (tính chất). Vậy A đúng.
Gọi H là giao điểm của BC và AO.
Xét tam giác BOH và tam giác COH có:
OB = OC
\(\widehat {BOH} = \widehat {COH}\) (tính chất hai tiếp tuyến cắt nhau)
OH chung
nên \(\Delta BOH = \Delta COH\) suy ra \(\widehat {BHO} = \widehat {CHO}\).
Mà hai góc kề bù nên \(\widehat {BHO} = \widehat {CHO} = \frac{1}{2}.180^\circ = 90^\circ \).
Suy ra \(OA \bot BC\). Vậy B đúng.
Vì BH = HC (hai cạnh tương ứng) và \(OA \bot BC\) nên OA là đường trung trực của BC. Vậy C đúng.
Vậy D sai.
Đáp án D.
a) Quy đồng, rút gọn.
b) Đưa biểu thức về dạng \(A\left( x \right) + \frac{C}{{B\left( x \right)}}\) với C là hằng số. Để biểu thức đó là số nguyên thì \(B\left( x \right) \in \) Ư(C).
c) Nhận xét mẫu số trước khi giải bất phương trình, lưu ý kết hợp điều kiện.
a) Với \(x \ge 0,x \ne 4,x \ne 9.\) Ta có:
\(A = \left( {1 - \frac{{\sqrt x }}{{1 + \sqrt x }}} \right):\left( {\frac{{\sqrt x {\rm{\;}} + 3}}{{\sqrt x {\rm{\;}} - 2}} + \frac{{\sqrt x {\rm{\;}} + 2}}{{3 - \sqrt x }} + \frac{{\sqrt x {\rm{\;}} + 2}}{{x - 5\sqrt x {\rm{\;}} + 6}}} \right)\)
\(A = \frac{1}{{\sqrt x {\rm{\;}} + 1}}:\left( {\frac{{\left( {\sqrt x {\rm{\;}} + 3} \right)\left( {\sqrt x {\rm{\;}} - 3} \right)}}{{\left( {\sqrt x {\rm{\;}} - 2} \right)\left( {\sqrt x {\rm{\;}} - 3} \right)}} - \frac{{\left( {\sqrt x {\rm{\;}} + 2} \right)\left( {\sqrt x {\rm{\;}} - 2} \right)}}{{\left( {\sqrt x {\rm{\;}} - 2} \right)\left( {\sqrt x {\rm{\;}} - 3} \right)}} + \frac{{\sqrt x {\rm{\;}} + 2}}{{\left( {\sqrt x {\rm{\;}} - 2} \right)\left( {\sqrt x {\rm{\;}} - 3} \right)}}} \right)\)
\(A = \frac{1}{{\sqrt x {\rm{\;}} + 1}}:\frac{{x - 9 - \left( {x - 4} \right) + \sqrt x {\rm{\;}} + 2}}{{\left( {\sqrt x {\rm{\;}} - 2} \right)\left( {\sqrt x {\rm{\;}} - 3} \right)}}\)
\(A = \frac{1}{{\sqrt x {\rm{\;}} + 1}}:\frac{{\sqrt x {\rm{\;}} - 3}}{{\left( {\sqrt x {\rm{\;}} - 2} \right)\left( {\sqrt x {\rm{\;}} - 3} \right)}}\)
\(A = \frac{1}{{\sqrt x {\rm{\;}} + 1}}:\frac{1}{{\sqrt x {\rm{\;}} - 2}} = \frac{{\sqrt x {\rm{\;}} - 2}}{{\sqrt x {\rm{\;}} + 1}}.\)
b) \(A = \frac{{\sqrt x {\rm{\;}} - 2}}{{\sqrt x {\rm{\;}} + 1}} = \frac{{\sqrt x + 1 - 3}}{{\sqrt x {\rm{\;}} + 1}} = 1 - \frac{3}{{\sqrt x {\rm{\;}} + 1}}\left( {x \ge 0} \right)\)
Để \(A \in \mathbb{Z}\) với x nguyên thì \(\sqrt x {\rm{\;}} + 1\) là ước nguyên dương của 3 do \(\sqrt x {\rm{\;}} + 1 > 0\)
Ư(3) = {1;3} nên:
+) Với \(\sqrt x {\rm{\;}} + 1 = 1\) suy ra \(\sqrt x = 0\) nên \(x = 0\) (TM).
+) Với \(\sqrt x {\rm{\;}} + 1 = 3\) suy ra \(\sqrt x = 2\) nên \(x = 4\) (KTM).
Vậy với \(x = 0\) thì \(A \in \mathbb{Z}\).
c) Vì \(A < 0\) nên \(\frac{{\sqrt x {\rm{\;}} - 2}}{{\sqrt x {\rm{\;}} + 1}} < 0\).
Do \(\sqrt x {\rm{\;}} + 1 > 0\) nên \(\frac{{\sqrt x {\rm{\;}} - 2}}{{\sqrt x {\rm{\;}} + 1}} < 0\) khi \(\sqrt x {\rm{\;}} - 2 < 0\) hay \(x < 4\).
Kết với \(x \ge 0\), suy ra \(A < 0\) khi \(0 \le x < 4\).
Vậy \(0 \le x < 4\) thì \(A < 0.\)
Gọi giá tiền một quả trứng gà và một quả trứng vịt lần lượt là \(x\) và \(y\) đồng (\(x;y \in \mathbb{N}\))
Dựa vào đề bài lập hệ phương trình.
Giải hệ phương trình đó để tính giá tiền một quả trứng gà và một quả trứng vịt.
Từ đó tính số tiền mua \(62\) quả trứng gồm \(22\) quả trứng gà và \(40\) quả trứng vịt.
Gọi giá tiền một quả trứng gà và một quả trứng vịt lần lượt là \(x\) và \(y\) đồng (\(x;y \in \mathbb{N}\))
Vì mua \(24\) quả trứng gà và \(13\) quả trứng vịt hết \(91200\) đồng nên ta có phương trình:
\(24x + 13y = 91200\).
Vì mua \(48\) quả trứng gà và \(36\) quả trứng vịt hết \(206400\) đồng nên ta có phương trình:
\(48x + 36y = 206400\) hay \(4x + 3y = 17200\).
Ta có hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{24x + 13y = 91200}\\{4x + 3y = 17200}\end{array}} \right.\)
\(\begin{array}{l}\left\{ {\begin{array}{*{20}{l}}{24x + 13y = 91200}\\{24x + 18y = 103200}\end{array}} \right.\\\left\{ \begin{array}{l}5y = 12000\\4x + 3y = 17200\end{array} \right.\\\left\{ \begin{array}{l}y = 2400\\4x + 3.2400 = 17200\end{array} \right.\\\left\{ \begin{array}{l}y = 2400(TM)\\x = 2500(TM)\end{array} \right.\end{array}\)
Vậy số tiền mua \(22\) quả trứng gà và \(40\) quả trứng vịt là: \(2500.22 + 2400.40 = 151000\) đồng.
Phân tích đề bài: Phần diện tích cần tính là hình vành khuyên. Kích cỡ đeo nhẫn chính là đường kính của đường tròn nhỏ, còn thước kẹp pan-me đo được đường kính của đường tròn lớn.
Tính bán kính hai đường tròn đồng tâm đó.
Sử dụng công thức tính diện tích hình vành khuyên giới hạn bởi hai đường tròn \(\left( {O;R} \right)\) và \(\left( {O;r} \right)\) với \(R > r\) là:
\(S = \pi .\left( {{R^2} - {r^2}} \right)\)
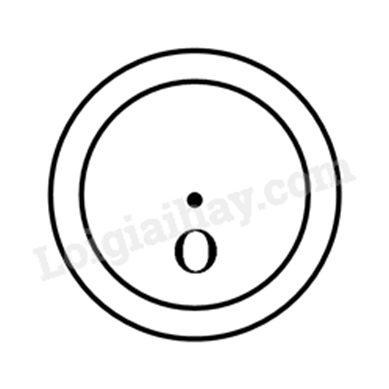
Bán kính của hai đường tròn nhỏ và lớn lần lượt là: \(\frac{{15}}{2} = 7,5\left( {mm} \right)\) và \(\frac{{17}}{2} = 8,5\left( {mm} \right)\)
Phần diện tích cần tính là diện tích của hình vành khuyên tạo bởi hai đường tròn đồng tâm O có đường kính lần lượt là 17mm và 15mm.
Vậy diện tích bề mặt là:
\(S = \pi \left( {8,{5^2} - 7,{5^2}} \right) \approx 3,14.16 = 50,24\left( {m{m^2}} \right)\)
Vậy diện tích một bề mặt của chiếc nhẫn là \(50,24m{m^2}\).
a) Chứng minh tam giác ACH và tam giác CHB vuông nên viết các hệ thức lượng liên quan đến cạnh CH.
Chứng minh \(\widehat {CAB} = \widehat {HCB}\) nên \(\cos \widehat {CAB} = \cos \widehat {HCB}\) suy ra điều phải chứng minh.
b) Chứng minh \(\Delta IAO = \Delta ICO\left( {c.c.c} \right)\) suy ra \(\widehat {IOA} = \widehat {ICO} = 90^\circ \) hay \(IC \bot OC\) tại C.
c) Chứng minh \(\Delta AIO = \Delta CIO\) và \(\Delta KCO = \Delta KBO\).
Biểu diễn \({S_{AIKB}}\) theo \({S_{\Delta IOK}}\).
Suy ra diện tích nhỏ nhất của \({S_{AIKB}}\) theo R.
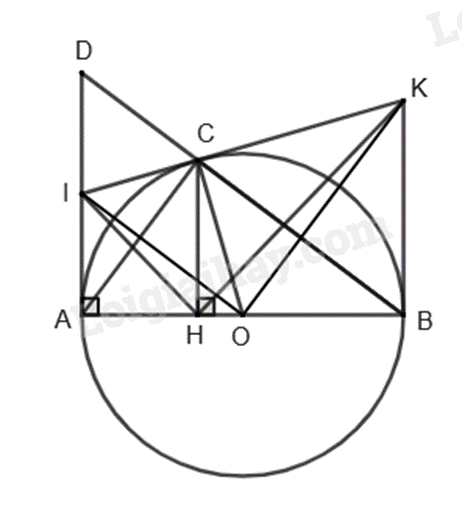
a) Vì AB là đường kính của (O) và \(C \in \left( O \right)\) suy ra \(\Delta ABC\) vuông tại C.
Vì CH vuông góc với AB tại H nên theo hệ thức lượng trong tam giác vuông, ta có:
\(CH = AC.\sin A\) (tam giác ACH vuông tại H)
và \(CH = BC.\cos \widehat {HCB}\) (tam giác CHB vuông tại H).
Mà \(\widehat {CAB} = \widehat {HCB}\) (cùng phụ với \(\widehat {ACH}\)) nên \(\cos \widehat {CAB} = \cos \widehat {HCB}\) hay \(\cos A = \cos \widehat {HCB}\). Do đó \(CH = BC.\cos A\).
Do đó \(C{H^2} = \left( {AC.\sin A} \right)\left( {BC.\cos A} \right) = AC.BC.\sin A.\cos A\).
b) Ta có \(CI = IA = ID\) (đường trung truyến trong tam giác vuông)
Xét tam giác IAO và tam giác ICO có:
AO = OC = R
IA = IC (cmt)
OI chung
Suy ra \(\Delta IAO = \Delta ICO\left( {c.c.c} \right)\), do đó \(\widehat {IOA} = \widehat {ICO} = 90^\circ \) hay \(IC \bot OC\) tại C.
Vậy IC là tiếp tuyến của (O) tại điểm C.
c) Theo ý b, ta có \(\Delta AIO = \Delta CIO\) (c.c.c).
Chứng minh tương tự, ta có \(\Delta KCO = \Delta KBO\) (c.c.c).
Mà \({S_{AIKB}} = {S_{\Delta AIO}} + {S_{\Delta CIO}} + {S_{\Delta COK}} + {S_{\Delta KOB}} = 2\left( {{S_{\Delta CIO}} + {S_{\Delta COK}}} \right)\)
Suy ra \({S_{AIKB}} = 2.{S_{\Delta IOK}} = OC.IK = R.IK \ge R.AB = R.2R = 2{R^2}\)
Dấu “=” xảy ra khi IK = AB. Khi đó C là điểm chính giữa $\overset\frown{AB}$.
Vậy \({S_{AIKB}}\) có giá trị lớn nhất là \(2{R^2}\) khi C là điểm chính giữa $\overset\frown{AB}$.
Sử dụng công thức \(k\sqrt {k - 1} + \left( {k - 1} \right)\sqrt k {\mkern 1mu} = \sqrt {k\left( {k - 1} \right)} \left( {\sqrt k + \sqrt {k - 1} } \right)\) với \(k \ge 1\).
Ta có:
\(\begin{array}{l}k\sqrt {k - 1} + \left( {k - 1} \right)\sqrt k {\mkern 1mu} \\ = \sqrt k .\sqrt {k - 1} .\left( {\sqrt k + \sqrt {k - 1} } \right)\end{array}\)
\( = \sqrt {k\left( {k - 1} \right)} \left( {\sqrt k + \sqrt {k - 1} } \right)\) với \(k \ge 1\).
Suy ra
\(\begin{array}{l}\frac{1}{{k\sqrt {k - 1} + \left( {k - 1} \right)\sqrt k }}\\ = \frac{1}{{\sqrt {k\left( {k - 1} \right)} \left( {\sqrt k + \sqrt {k - 1} } \right)}}\\ = \frac{{\left( {\sqrt k - \sqrt {k - 1} } \right)}}{{\sqrt {k\left( {k - 1} \right)} \left( {\sqrt k + \sqrt {k - 1} } \right)\left( {\sqrt k - \sqrt {k - 1} } \right)}}\end{array}\)
\(\begin{array}{l} = \frac{{\sqrt k - \sqrt {k - 1} }}{{\sqrt {k\left( {k - 1} \right)} }}\\ = \frac{{\sqrt k - \sqrt {k - 1} }}{{\sqrt k .\sqrt {k - 1} }}\\ = \frac{1}{{\sqrt {k - 1} }} - \frac{1}{{\sqrt k }}\end{array}\)
Thay lại vào A ta được:
\(A = \frac{1}{{2\sqrt 1 + 1\sqrt 2 }} + \frac{1}{{3\sqrt 2 + 2\sqrt 3 }} + ... + \frac{1}{{2025\sqrt {2024} + 2024\sqrt {2025} }}\)\({\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = {\mkern 1mu} \left( {\frac{1}{{\sqrt 1 }} - \frac{1}{{\sqrt 2 }}} \right) + \left( {\frac{1}{{\sqrt 2 }} - \frac{1}{{\sqrt 3 }}} \right) + ..... + \left( {\frac{1}{{\sqrt {2024} }} - \frac{1}{{\sqrt {2025} }}} \right)\)
\({\mkern 1mu} = 1 - \frac{1}{{\sqrt {2025} }} = 1 - \frac{1}{{45}} = \frac{{44}}{{45}}\).
Vậy \(A = \frac{{44}}{{45}}\).
Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau:
Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau:
Phần I. Câu hỏi trắc nghiệm nhiều phương án lựa chọn Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau:
A. NỘI DUNG ÔN TẬP B. BÀI TẬP I. Phần trắc nghiệm
Các bài khác cùng chuyên mục
- Đề khảo sát chất lượng đầu năm Toán 9 THCS&THPT Lương Thế Vinh - Hà Nội
- Đề khảo sát chất lượng đầu năm Toán 9 THCS Thuận Thành – Bắc Ninh
- Đề khảo sát chất lượng đầu năm Toán 9 THCS – THPT Tạ Quang Bửu – Hà Nội
- Đề khảo sát chất lượng đầu năm Toán 9 THCS – THPT Newton - Hà Nội
- Đề thi học kì 2 Toán 9 - Đề số 5
- Đề khảo sát chất lượng đầu năm Toán 9 THCS&THPT Lương Thế Vinh - Hà Nội
- Đề khảo sát chất lượng đầu năm Toán 9 THCS Thuận Thành – Bắc Ninh
- Đề khảo sát chất lượng đầu năm Toán 9 THCS – THPT Tạ Quang Bửu – Hà Nội
- Đề khảo sát chất lượng đầu năm Toán 9 THCS – THPT Newton - Hà Nội
- Đề thi học kì 2 Toán 9 - Đề số 5










Danh sách bình luận