Đề thi giữa kì 2 Toán 9 - Đề số 1
Phần I. Câu hỏi trắc nghiệm nhiều phương án lựa chọn (3 điểm) Thí sinh trả lời từ câu 1 đến câu 6. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Đề bài
Trong các hàm số sau hàm số nào có dạng \(y = a{x^2}\) với \(a \ne 0\)
-
A.
\(y = 7{x^3} - 4{x^2}\).
-
B.
\(y = 3x - 3\).
-
C.
\(y = - 4{x^2}\).
-
D.
\(y = \sqrt {6x + 3} \).
Cho phương trình bậc hai \( - 4{x^2} + 3x - 6 = 0\). Phương trình có nghiệm là
-
A.
Phương trình vô nghiệm.
-
B.
Phương trình có nghiệm kép \({x_1} = {x_2} = \frac{3}{8}\).
-
C.
Phương trình có hai nghiệm phân biệt là \({x_1} = \frac{3}{8}\), \({x_2} = - \frac{3}{8}\).
-
D.
Phương trình có hai nghiệm phân biệt là \({x_1} = \frac{3}{4}\), \({x_2} = - \frac{3}{4}\).
Cho \(u + v = - 4\) và \(u.v = - 21\), \(u < v\). Giá trị của \(u\) là
-
A.
\( - 4\).
-
B.
\( - 9\).
-
C.
\(0\).
-
D.
\( - 7\).
-
A.
6.
-
B.
7.
-
C.
8.
-
D.
9.
Một đường tròn là đường tròn nội tiếp nếu nó:
-
A.
Đi qua các đỉnh của một tam giác.
-
B.
Tiếp xúc với các đường thẳng chứa các cạnh của tam giác.
-
C.
Tiếp xúc với các cạnh của tam giác.
-
D.
Nằm trong một tam giác.
Tứ giác \(ABCD\) nội tiếp đường tròn. Biết sđ$\overset\frown{BD}=140{}^\circ $ và \(\widehat {BAD} < 90^\circ \), tính \(\widehat {BCD}\).
-
A.
\(100^\circ \).
-
B.
\(110^\circ \).
-
C.
\(70^\circ \).
-
D.
\(20^\circ \).
Trong môn Sinh học, một lớp 9 khảo sát về nhóm máu của các học sinh trong lớp. Kết quả khảo sát được trình bày như sau:
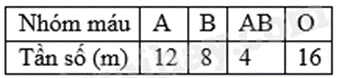
a) Số học sinh tham gia khảo sát là 40.
b) Số học sinh có nhóm máu A là ít nhất.
c) Tần số tương đối của nhóm máu AB là 30%.
d) Biểu đồ tần số tương đối về nhóm máu của các học sinh trong lớp như sau:
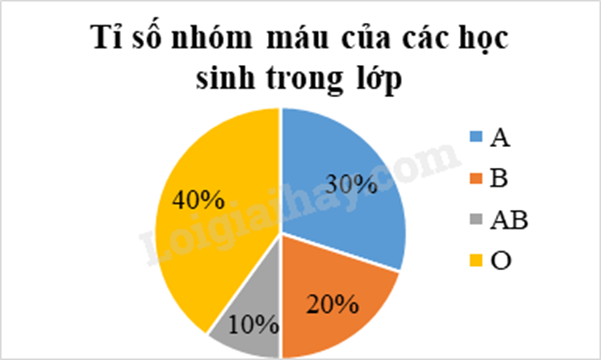
Cho đường tròn \(\left( O \right)\) đường kính \(AB\). Gọi \(H\) là điểm nằm giữa \(O\) và \(B\) (H không là trung điểm của OB). Kẻ dây \(CD\) vuông góc với \(AB\) tại \(H\). Trên cung nhỏ \(AC\) lấy điểm \(E\), kẻ \(CK\) vuông góc với \(AE\) tại \(K\). Đường thẳng \(DE\) cắt \(CK\) tại \(F\).
a) \(AHCK\) là tứ giác nội tiếp.
b) \(\widehat {EAO} + \widehat {HCK} = 90^\circ \).
c) \(\widehat {KAC} = \widehat {EDC}\).
d) \(AH.AB = A{C^2}\).
Giá trị của hàm số \(y = - 3{x^2}\) tại \({x_0} = - 3\) bằng …
Đáp án:
Phương trình \({x^2} + ax + b = 0\) (với a, b là các số nguyên) có một nghiệm là \(5 + \sqrt {21} \). Tổng của a và b là:
Đáp án:
Trong 3 ngày từ 21 – 23/8/2023 hệ thống cửa hàng của BiTi’s tại Hải Phòng đã thống kê số lượng bán được của mẫu giày phiên bản BITI’S HUNTER X LITEFLEX 3.0 theo bảng số liệu sau:
Tần số tương đối của cỡ giày số 39 (làm tròn kết quả đến hàng phần mười) là:
(không điền dấu %)
Đáp án:
Cho tam giác ABC vuông cân tại A, có \(AC = 5\sqrt 2 cm\). Bán kính đường tròn ngoại tiếp tam giác ABC bằng …
Đáp án:
Lời giải và đáp án
Trong các hàm số sau hàm số nào có dạng \(y = a{x^2}\) với \(a \ne 0\)
-
A.
\(y = 7{x^3} - 4{x^2}\).
-
B.
\(y = 3x - 3\).
-
C.
\(y = - 4{x^2}\).
-
D.
\(y = \sqrt {6x + 3} \).
Đáp án : C
Xác định xem hàm số nào có dạng \(y = a{x^2}\).
Hàm số \(y = - 4{x^2}\) có dạng \(y = a{x^2}\).
Đáp án C
Cho phương trình bậc hai \( - 4{x^2} + 3x - 6 = 0\). Phương trình có nghiệm là
-
A.
Phương trình vô nghiệm.
-
B.
Phương trình có nghiệm kép \({x_1} = {x_2} = \frac{3}{8}\).
-
C.
Phương trình có hai nghiệm phân biệt là \({x_1} = \frac{3}{8}\), \({x_2} = - \frac{3}{8}\).
-
D.
Phương trình có hai nghiệm phân biệt là \({x_1} = \frac{3}{4}\), \({x_2} = - \frac{3}{4}\).
Đáp án : A
Xác định \(\Delta = {b^2} - 4ac\) để xác định nghiệm của phương trình.
(Ta cũng có thể sử dụng máy tính cầm tay để xác định nghiệm)
Hệ số \(a = - 4,b = 3,c = - 6\). Ta có \(\Delta = {b^2} - 4.a.c = - 87 < 0\) nên phương trình vô nghiệm.
Đáp án A
Cho \(u + v = - 4\) và \(u.v = - 21\), \(u < v\). Giá trị của \(u\) là
-
A.
\( - 4\).
-
B.
\( - 9\).
-
C.
\(0\).
-
D.
\( - 7\).
Đáp án : D
Xác định phương trình khi biết tổng và tích:
Nếu hai số có tổng bằng S và tích bằng P thì hai số đó là hai nghiệm của phương trình bậc hai: \(x^2 − Sx + P = 0\). Điều kiện để có hai số đó là \(S^2 − 4P \ge 0\)
Từ đó giải phương trình tìm u. (đối với bài tập trắc nghiệm có thể bấm máy tính cầm tay)
Hai số cần tìm là nghiệm của phương trình \({x^2} + 4x - 21 = 0\)
Giải ta được \(u = - 7\) và \(v = 3\).
Đáp án D
-
A.
6.
-
B.
7.
-
C.
8.
-
D.
9.
Đáp án : D
Quan sát bảng tần số để xác định tần số xuất hiện của mặt ba chấm.
Tần số xuất hiện của mặt ba chấm là 9.
Đáp án D
Một đường tròn là đường tròn nội tiếp nếu nó:
-
A.
Đi qua các đỉnh của một tam giác.
-
B.
Tiếp xúc với các đường thẳng chứa các cạnh của tam giác.
-
C.
Tiếp xúc với các cạnh của tam giác.
-
D.
Nằm trong một tam giác.
Đáp án : C
Dựa vào khái niệm đường tròn nội tiếp tam giác:
Theo khái niệm, đường tròn nội tiếp tam giác là đường tròn tiếp xúc với tất cả các cạnh của tam giác nên đáp án C đúng.
Đáp án C
Tứ giác \(ABCD\) nội tiếp đường tròn. Biết sđ$\overset\frown{BD}=140{}^\circ $ và \(\widehat {BAD} < 90^\circ \), tính \(\widehat {BCD}\).
-
A.
\(100^\circ \).
-
B.
\(110^\circ \).
-
C.
\(70^\circ \).
-
D.
\(20^\circ \).
Đáp án : B
Ta tính \(\widehat {BAD}\) thông qua số đo cung BD: Số đo góc nội tiếp bằng một nửa số đo cung nhỏ đó.
Sử dụng định lí tổng hai góc đối của tứ giác nội tiếp bằng \(180^\circ \) để tính \(\widehat {BCD}\).
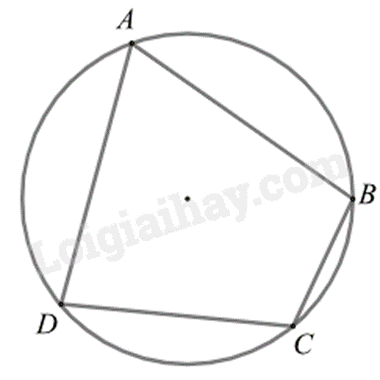
Vì tứ giác ABCD nội tiếp đường tròn nên \(\widehat {BAD}\) chắn cung BD.
Mà \(\widehat {BAD} < 90^\circ \) nên \(\widehat {BAD} = \) \(\frac{1}{2}\)sđ$\overset\frown{BD}$\( = \frac{1}{2}.140^\circ = 70^\circ \) (góc nội tiếp chắn cung BD).
Vì tứ giác ABCD nội tiếp đường tròn nên \(\widehat {BAD} + \widehat {BCD} = 180^\circ \), suy ra \(\widehat {BCD} = 180^\circ - \widehat {BAD} = 180^\circ - 70^\circ = 110^\circ \)
Đáp án B
Trong môn Sinh học, một lớp 9 khảo sát về nhóm máu của các học sinh trong lớp. Kết quả khảo sát được trình bày như sau:
a) Số học sinh tham gia khảo sát là 40.
b) Số học sinh có nhóm máu A là ít nhất.
c) Tần số tương đối của nhóm máu AB là 30%.
d) Biểu đồ tần số tương đối về nhóm máu của các học sinh trong lớp như sau:
a) Số học sinh tham gia khảo sát là 40.
b) Số học sinh có nhóm máu A là ít nhất.
c) Tần số tương đối của nhóm máu AB là 30%.
d) Biểu đồ tần số tương đối về nhóm máu của các học sinh trong lớp như sau:
a) Số học sinh tham gia khảo sát bằng tổng tần số của các nhóm máu.
b) So sánh tần số các nhóm máu.
c) Tần số tương đối của giá trị bằng tần số của giá trị với tổng tần số.
d) Tính tần số tương đối và vẽ biểu đồ tần số tương đối về nhóm máu của các học sinh trong lớp.
a) Đúng
Số học sinh tham gia khảo sát là:
12 + 8 + 4 + 16 = 40.
b) Sai
Quan sát bảng tần số, ta thấy tần số của nhóm máu AB nhỏ nhất nên số học sinh có nhóm máu AB là ít nhất.
c) Sai
Tần số tương đối của nhóm máu AB là:
\(\frac{4}{{40}}.100\% = 10\% \).
d) Đúng
Từ bảng tần số, ta có bảng tần số tương đối như sau:
Biểu đồ tần số tương đối về nhóm máu của các học sinh trong lớp là:
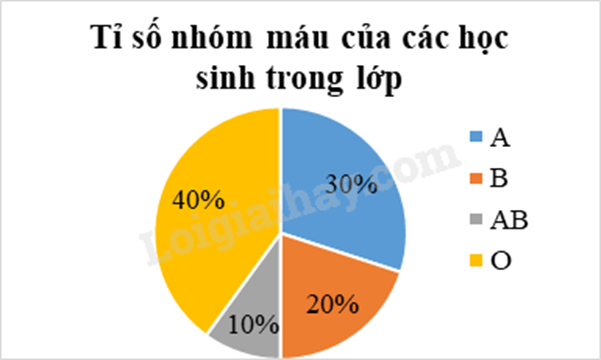
Đáp án ĐSSĐ
Cho đường tròn \(\left( O \right)\) đường kính \(AB\). Gọi \(H\) là điểm nằm giữa \(O\) và \(B\) (H không là trung điểm của OB). Kẻ dây \(CD\) vuông góc với \(AB\) tại \(H\). Trên cung nhỏ \(AC\) lấy điểm \(E\), kẻ \(CK\) vuông góc với \(AE\) tại \(K\). Đường thẳng \(DE\) cắt \(CK\) tại \(F\).
a) \(AHCK\) là tứ giác nội tiếp.
b) \(\widehat {EAO} + \widehat {HCK} = 90^\circ \).
c) \(\widehat {KAC} = \widehat {EDC}\).
d) \(AH.AB = A{C^2}\).
a) \(AHCK\) là tứ giác nội tiếp.
b) \(\widehat {EAO} + \widehat {HCK} = 90^\circ \).
c) \(\widehat {KAC} = \widehat {EDC}\).
d) \(AH.AB = A{C^2}\).
a) Chứng minh bốn điểm A, H, C, K thuộc cùng một đường tròn nên AHCK là tứ giác nội tiếp.
b) Dựa vào định lí tổng hai góc đối của tứ giác nội tiếp.
c) Dựa vào kiến thức về góc nội tiếp: Hai góc nội tiếp cùng chắn một cung thì bằng nhau.
d) Sử dụng kiến thức về góc nội tiếp chắn nửa đường tròn là góc vuông.
Chứng minh $\Delta AHC\backsim \Delta ACB\left( g.g \right)$ suy ra tỉ số cạnh bằng nhau.
a) Đúng
Xét tam giác ACK vuông tại K (\(CK \bot AE\) tại K) nên K thuộc đường tròn đường kính AC.
Xét tam giác ACH vuông tại H (\(CD \bot AB\) tại H) nên H thuộc đường tròn đường kính AC.
Do đó bốn điểm A, H, C, K thuộc đường tròn đường kính AC hay tứ giác AHCK là tứ giác nội tiếp.
b) Sai
Vì tứ giác \(AHCK\) là tứ giác nội tiếp nên \(\widehat {EAO} + \widehat {HCK} = 180^\circ \) (tính chất tứ giác nội tiếp) nên b sai.
c) Đúng
Ta có: \(\widehat {EAC} = \widehat {EDC}\) (hai góc nội tiếp chắn cung EC) hay \(\widehat {KAC} = \widehat {EDC}\).
d) Đúng
Xét đường tròn \(\left( O \right)\) đường kính \(AB\) có \(\widehat {ACB} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)
Suy ra \(\Delta ACB\) vuông tại C.
Xét \(\Delta AHC\) và \(\Delta ACB\) có:
\(\widehat A\) chung
\(\widehat {AHC} = \widehat {ACB}\left( { = 90^\circ } \right)\)
Suy ra $\Delta AHC\backsim \Delta ACB\left( g.g \right)$
Do đó \(\frac{{AH}}{{AC}} = \frac{{AC}}{{AB}}\) nên \(AH.AB = A{C^2}\)
Đáp án ĐSĐĐ
Giá trị của hàm số \(y = - 3{x^2}\) tại \({x_0} = - 3\) bằng …
Đáp án:
Đáp án:
Thay \({x_0} = - 3\) vào hàm số để tìm \(y\).
Thay \({x_0} = - 3\) vào hàm số, ta được: \(y = - 3.{\left( { - 3} \right)^2} = - 3.9 = - 27\).
Đáp án: -27
Phương trình \({x^2} + ax + b = 0\) (với a, b là các số nguyên) có một nghiệm là \(5 + \sqrt {21} \). Tổng của a và b là:
Đáp án:
Đáp án:
Thay nghiệm \(5 + \sqrt {21} \) vào phương trình, lập hệ phương trình hai ẩn a, b để tìm a, b.
Áp dụng định lí Viète để vào phương trình tìm được để tìm nghiệp còn lại.
Gọi \({x_1};{x_2}\) là hai nghiệm của phương trình \({x^2} + ax + b = 0\) (1).
Không mất tính tổng quát, giả sử \({x_1} = 5 + \sqrt {21} \) và \({x_2}\) là nghiệm còn lại.
Thay \(x = {x_1} = 5 + \sqrt {21} \) và (1) ta được:
\(\begin{array}{l}{\left( {5 + \sqrt {21} } \right)^2} + a\left( {5 + \sqrt {21} } \right) + b = 0\\46 + 10\sqrt {21} + 5a + \sqrt {21} a + b = 0\\\left( {a + 10} \right)\sqrt {21} + \left( {5a + b + 46} \right) = 0\end{array}\)
Vì a, b là các số nguyên nên ta có hệ:
\(\begin{array}{l}\left\{ \begin{array}{l}a + 10 = 0\\5a + b + 46 = 0\end{array} \right.\\\left\{ \begin{array}{l}a = - 10\\b = - 46 - 5a\end{array} \right.\\\left\{ \begin{array}{l}a = - 10\\b = 4\end{array} \right.\end{array}\)
Suy ra phương trình (1) là \({x^2} - 10x + 4 = 0\)
Ta có: \(a + b = - 10 + 4 = - 6\)
Đáp án: -6
Trong 3 ngày từ 21 – 23/8/2023 hệ thống cửa hàng của BiTi’s tại Hải Phòng đã thống kê số lượng bán được của mẫu giày phiên bản BITI’S HUNTER X LITEFLEX 3.0 theo bảng số liệu sau:
Tần số tương đối của cỡ giày số 39 (làm tròn kết quả đến hàng phần mười) là:
(không điền dấu %)
Đáp án:
Đáp án:
Xác định tần số của cỡ giày số 39 và tổng các tần số.
Tần số tương đối của giá trị bằng tỉ số phần trăm giữa tần số của giá trị với tổng tần số.
Quan sát bảng trên ta thấy cỡ giày 39 có số lần xuất hiện là 154.
Tổng các tần số là 969.
Khi đó tần số tương đối của cỡ giày số 39 là: \(\frac{{154}}{{969}}.100\% \approx 15,9\% \)
Đáp án: 15,9
Cho tam giác ABC vuông cân tại A, có \(AC = 5\sqrt 2 cm\). Bán kính đường tròn ngoại tiếp tam giác ABC bằng …
Đáp án:
Đáp án:
Đường tròn ngoại tiếp tam giác vuông cân có bán kính bằng một nửa cạnh huyền của tam giác vuông cân.
Tam giác ABC vuông cân tại A nên \(AB = AC = 5\sqrt 2 cm\).
Áp dụng định lí Pythagore vào tam giác ABC, ta có:
\(BC = \sqrt {{{\left( {5\sqrt 2 } \right)}^2} + {{\left( {5\sqrt 2 } \right)}^2}} = 10\left( {cm} \right)\).
Vì tam giác ABC vuông tại A nên đường tròn ngoại tiếp tam giác ABC có đường kính là cạnh huyền BC.
Bán kính đường tròn ngoại tiếp tam giác ABC là: \(10:2 = 5\left( {cm} \right)\)
Đáp án: 5
Gọi vận tốc dự định của bác An đi từ nhà đến nơi làm việc là \(x\left( {km/h,x > 10} \right)\), biểu diễn vận tốc đi quãng đường còn lại theo \(x\).
Lập các biểu thức biểu diễn thời gian bác An đi \(\frac{1}{3}\) quãng đường đầu và quãng đường còn lại.
Từ đó lập phương trình bậc hai ẩn \(x\) biểu diễn thời gian đi của bác An.
Giải phương trình, kết hợp điều kiện ban đầu của \(x\) để xác định.
Đổi 20 phút = \(\frac{1}{3}\) giờ.
Gọi vận tốc dự định của bác An đi từ nhà đến nơi làm việc là \(x\left( {km/h,x > 10} \right)\).
Khi đó vận tốc bác An đi quãng đường còn lại là: \(x - 10\left( {km/h,x > 10} \right)\)
Thời gian bác An dự định đi từ nhà đến nơi làm việc là: \(\frac{{60}}{x}\) (giờ)
Thời gian bác An đi \(\frac{1}{3}\) quãng đường đầu là: \(\frac{1}{3}.\frac{{60}}{x} = \frac{{20}}{x}\) (giờ)
Quãng đường còn lại là: \(60.\left( {1 - \frac{1}{3}} \right) = 40\) (km)
Thời gian bác An đi quãng đường còn lại là: \(\frac{{40}}{{x - 10}}\) (giờ).
Vì bác An đến nơi làm việc muộn hơn dự định 20 phút nên ta có phương trình:
\(\frac{{20}}{x} + \frac{{40}}{{x - 10}} = \frac{{60}}{x} + \frac{1}{3}\)
\(\frac{{40}}{{x - 10}} = \frac{{40}}{x} + \frac{1}{3}\)
\({x^2} - 10x - 1200 = 0\)
Giải phương trình ta được \({x_1} = 40\) (tm); \({x_2} = - 30\) (không tm).
Vậy vận tốc dự định của bác An khi đi từ nhà đến nơi làm việc là 40km/h.
Tính khoảng cách giữa hai vị trí A và B chính là tìm cạnh của tam giác đều ABC khi biết bán kính đường tròn ngoại tiếp tam giác.
Đường tròn ngoại tiếp tam giác đều cạnh a có tâm là trọng tâm của tam giác đó và bán kính bằng \(\frac{{\sqrt 3 }}{3}a\).
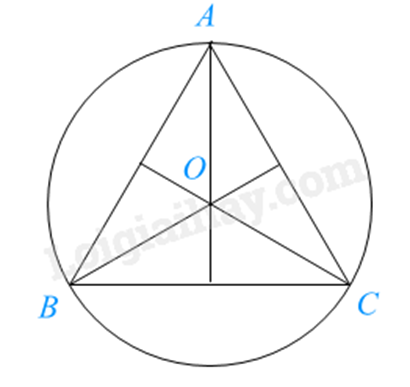
Gọi tâm đường tròn ngoại tiếp tam giác ABC là O. Vì tam giác ABC đều nên bán kính đường tròn ngoại tiếp tam giác ABC bằng \(\frac{{\sqrt 3 }}{3}AB\), hay \(OA = \frac{{\sqrt 3 }}{3}AB\).
Suy ra \(AB = OA:\frac{{\sqrt 3 }}{3} = 6:\frac{{\sqrt 3 }}{3} = 6\sqrt 3 \) (dm)
Vậy khoảng cách A và B là \(6\sqrt 3 \) dm.
Xác định số nghiệm của phương trình sử dụng \(\Delta \) hoặc \(\Delta '\).
Áp dụng định lí Viète để tìm ra nghiệm \({x_2}\) còn lại.
Thay nghiệm vừa tìm được vào A.
Phương trình \(3{x^2} - 2x - 8 = 0\) có \(\Delta ' = {\left( { - 1} \right)^2} - 3.\left( { - 8} \right) = 25\) nên phương trình có hai nghiệm phân biệt.
Áp dụng định lí Viète, ta có: \({x_1}.{x_2} = \frac{{ - 8}}{3}\) suy ra \({x_2} = \frac{{ - 8}}{3}:2 = \frac{{ - 4}}{3}\).
Khi đó: \(A = 3.\frac{{ - 4}}{3} + 2025 = - 4 + 2025 = 2021\).
