Đề thi giữa kì 1 Toán 9 - Đề số 3
Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau: Câu 1: Nghiệm của phương trình \(x + 2y = 5\) là
Đề bài
Nghiệm của phương trình \(x + 2y = 5\) là
-
A.
\(\left( {x;y} \right) = \left( {1; - 2} \right)\).
-
B.
\(\left( {x;y} \right) = \left( {1;2} \right)\).
-
C.
\(\left( {x;y} \right) = \left( {2; - 1} \right)\).
-
D.
\(\left( {x;y} \right) = \left( {2;1} \right)\).
Cặp số nào sau đây là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}x + 2y = 3\\y = 1\end{array} \right.\)?
-
A.
\(\left( {x;y} \right) = \left( {1;2} \right)\).
-
B.
\(\left( {x;y} \right) = \left( {2;1} \right)\).
-
C.
\(\left( {x;y} \right) = \left( {1; - 1} \right)\).
-
D.
\(\left( {x;y} \right) = \left( {1;1} \right)\).
Nghiệm của phương trình \(x\left( {x + 1} \right) = 0\) là
-
A.
\(x = 0\) và \(x = - 1\).
-
B.
\(x = 1\).
-
C.
\(x = 0\).
-
D.
\(x = 1\) và \(x = - 1\).
Điều kiện xác định của phương trình \(\frac{{x + 3}}{{x - 1}} + \frac{{x - 2}}{x} = 2\) là
-
A.
\(x \ne 0;x \ne 1\).
-
B.
\(x = 0;x = 1\).
-
C.
\(x \ne 0\).
-
D.
\(x \ne 1\).
Cho \(a > b\), kết quả nào sau đây đúng?
-
A.
\(a + 3 > b + 5\).
-
B.
\(a - 2 > b - 2\).
-
C.
\( - 2a > - 2b\).
-
D.
\(2a > 3b\).
Cho \( - 2a \le - 2b\), kết quả nào sau đây là đúng?
-
A.
\(a \le b\).
-
B.
\(a - 2 \ge b - 1\).
-
C.
\(a > b\).
-
D.
\(2a \ge 2b\).
Trong các bất phương trình sau, bất phương trình nào không phải bất phương trình bậc nhất một ẩn?
-
A.
\(5x + 3 > 0\).
-
B.
\( - 2x + 7 < 0\).
-
C.
\(3x \le 0\).
-
D.
\(2{x^2} - 5 \ge 0\).
Trong các số sau, số nào là nghiệm của bất phương trình \(2 - 3x > 0\)?
-
A.
\( - 2\).
-
B.
\(2\).
-
C.
\(\frac{3}{2}\).
-
D.
\(\frac{2}{3}\).
Tỉ số lượng giác nào sau đây bằng \(\sin 40^\circ \)?
-
A.
\(\sin 50^\circ \).
-
B.
\(\cos 50^\circ \).
-
C.
\(\tan 50^\circ \).
-
D.
\(\cot 50^\circ \).
Cho tam giác ABC có AB = 5, AC = 12, BC = 13. Khi đó tỉ số lượng giác cosB là
-
A.
\(\frac{{13}}{5}\).
-
B.
\(\frac{5}{{13}}\).
-
C.
\(\frac{{12}}{5}\).
-
D.
\(\frac{5}{{12}}\).
Giá trị của biểu thức \({\sin ^2}25^\circ + {\cos ^2}25^\circ \) là
-
A.
0.
-
B.
1.
-
C.
2.
-
D.
3.
Cho tam giác ABC vuông tại A có BC = 10cm, \(\widehat C = 30^\circ \). Độ dài cạnh AB là:
-
A.
5,5cm.
-
B.
5cm.
-
C.
\(5\sqrt 3 \)cm.
-
D.
\(5\sqrt 2 \)cm.
Lời giải và đáp án
Nghiệm của phương trình \(x + 2y = 5\) là
-
A.
\(\left( {x;y} \right) = \left( {1; - 2} \right)\).
-
B.
\(\left( {x;y} \right) = \left( {1;2} \right)\).
-
C.
\(\left( {x;y} \right) = \left( {2; - 1} \right)\).
-
D.
\(\left( {x;y} \right) = \left( {2;1} \right)\).
Đáp án : B
Thay giá trị x, y vào phương trình để xác định nghiệm của phương trình.
Ta có: 1 + 2.2 = 5 nên \(\left( {x;y} \right) = \left( {1;2} \right)\) là một nghiệm của phương trình \(x + 2y = 5\).
Cặp số nào sau đây là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}x + 2y = 3\\y = 1\end{array} \right.\)?
-
A.
\(\left( {x;y} \right) = \left( {1;2} \right)\).
-
B.
\(\left( {x;y} \right) = \left( {2;1} \right)\).
-
C.
\(\left( {x;y} \right) = \left( {1; - 1} \right)\).
-
D.
\(\left( {x;y} \right) = \left( {1;1} \right)\).
Đáp án : D
Giải hệ phương trình để tìm nghiệm.
Ta có: \(\left\{ \begin{array}{l}x + 2y = 3\\y = 1\end{array} \right.\) suy ra \(\left\{ \begin{array}{l}x + 2.1 = 3\\y = 1\end{array} \right.\). Do đó \(\left\{ \begin{array}{l}x = 1\\y = 1\end{array} \right.\).
Đáp án D.
Nghiệm của phương trình \(x\left( {x + 1} \right) = 0\) là
-
A.
\(x = 0\) và \(x = - 1\).
-
B.
\(x = 1\).
-
C.
\(x = 0\).
-
D.
\(x = 1\) và \(x = - 1\).
Đáp án : A
Giải phương trình tích để tìm nghiệm.
Ta có: \(x\left( {x + 1} \right) = 0\)
+) \(x = 0\)
+) \(x + 1 = 0\) suy ra \(x = - 1\).
Vậy phương trình có hai nghiệm \(x = 0\) và \(x = - 1\).
Đáp án A.
Điều kiện xác định của phương trình \(\frac{{x + 3}}{{x - 1}} + \frac{{x - 2}}{x} = 2\) là
-
A.
\(x \ne 0;x \ne 1\).
-
B.
\(x = 0;x = 1\).
-
C.
\(x \ne 0\).
-
D.
\(x \ne 1\).
Đáp án : A
Điều kiện xác định của phương trình là mẫu thức khác 0.
Điều kiện xác định của phương trình \(\frac{{x + 3}}{{x - 1}} + \frac{{x - 2}}{x} = 2\) là:
\(x - 1 \ne 0\) và \(x \ne 0\)
hay \(x \ne 1\) và \(x \ne 0\).
Đáp án A.
Cho \(a > b\), kết quả nào sau đây đúng?
-
A.
\(a + 3 > b + 5\).
-
B.
\(a - 2 > b - 2\).
-
C.
\( - 2a > - 2b\).
-
D.
\(2a > 3b\).
Đáp án : B
Sử dụng tính chất của bất đẳng thức.
A. \(a + 3 > b + 5\)
Từ \(a > b\), ta cộng thêm 3 vào cả hai vế, ta có:
\(a + 3 > b + 3.\)
Mà \(b + 5 > b + 3\) nên chưa thể khẳng định được \(a + 3 > b + 5\). Vậy A sai.
B. \(a - 2 > b - 2\)
Từ \(a > b\), ta trừ đi 2 ở cả hai vế, ta có: \(a - 2 > b - 2.\)
Điều này đúng, vì trừ cùng một số ở hai vế không làm thay đổi bất đẳng thức. Vậy B đúng.
C. \( - 2a > - 2b\)
Từ \(a > b\), ta nhân cả hai vế với \( - 2\).
Khi nhân với một số âm, dấu bất đẳng thức sẽ đổi chiều, ta được: \( - 2a < - 2b.\) Vậy C sai.
D. \(2a > 3b\)
Từ \(a > b\), nhân cả hai vế với 2, ta được: \(2a > 2b.\)
Mà \(3b > 2b\), nên chưa thể khẳng định được \(2a > 3b\). Vậy D sai.
Đáp án B.
Cho \( - 2a \le - 2b\), kết quả nào sau đây là đúng?
-
A.
\(a \le b\).
-
B.
\(a - 2 \ge b - 1\).
-
C.
\(a > b\).
-
D.
\(2a \ge 2b\).
Đáp án : D
Sử dụng tính chất của bất đẳng thức.
Vì \( - 2a \le - 2b\) nên \(a \ge b\) (vì -2 < 0)
Nên A và C sai.
Vì \(a \ge b\) nên \(a - 2 \ge b - 2\).
Mà \(b - 1 \ge b - 2\) nên chưa thể khẳng định được \(a - 2 \ge b - 1\). Vậy B sai.
Vì \(a \ge b\) nên \(2a \ge 2b\) (vì 2 > 0) nên D đúng.
Đáp án D.
Trong các bất phương trình sau, bất phương trình nào không phải bất phương trình bậc nhất một ẩn?
-
A.
\(5x + 3 > 0\).
-
B.
\( - 2x + 7 < 0\).
-
C.
\(3x \le 0\).
-
D.
\(2{x^2} - 5 \ge 0\).
Đáp án : D
Bất phương trình bậc nhất một ẩn có dạng \(ax + b > 0\) (hoặc \(ax + b < 0,ax + b \ge 0,ax + b \le 0\)), \(a \ne 0\).
Bât phương trình \(2{x^2} - 5 \ge 0\) có bậc của x là 2 nên không phải phương trình bậc nhất một ẩn.
Đáp án D.
Trong các số sau, số nào là nghiệm của bất phương trình \(2 - 3x > 0\)?
-
A.
\( - 2\).
-
B.
\(2\).
-
C.
\(\frac{3}{2}\).
-
D.
\(\frac{2}{3}\).
Đáp án : A
Giải bất phương trình để tìm nghiệm.
Ta có: \(2 - 3x > 0\)
\(\begin{array}{l} - 3x > - 2\\x < \frac{2}{3}\end{array}\)
Trong các số trên, chỉ có \( - 2 < \frac{2}{3}\) nên -2 là một nghiệm của bất phương trình \(2 - 3x > 0\).
Đáp án A.
Tỉ số lượng giác nào sau đây bằng \(\sin 40^\circ \)?
-
A.
\(\sin 50^\circ \).
-
B.
\(\cos 50^\circ \).
-
C.
\(\tan 50^\circ \).
-
D.
\(\cot 50^\circ \).
Đáp án : B
Dựa vào tỉ số lượng giác của các góc phụ nhau: \(\sin \alpha = \cos \left( {90^\circ - \alpha } \right)\), \(\tan \alpha = \cot \left( {90^\circ - \alpha } \right)\).
Tỉ số lượng giác bằng \(\sin 40^\circ \) là \(\cos \left( {90^\circ - 40^\circ } \right) = \cos 50^\circ \).
Đáp án B.
Cho tam giác ABC có AB = 5, AC = 12, BC = 13. Khi đó tỉ số lượng giác cosB là
-
A.
\(\frac{{13}}{5}\).
-
B.
\(\frac{5}{{13}}\).
-
C.
\(\frac{{12}}{5}\).
-
D.
\(\frac{5}{{12}}\).
Đáp án : B
Chứng minh tam giác ABC vuông.
Từ đó biểu diễn tỉ số lượng giác cosB theo cạnh của tam giác ABC.
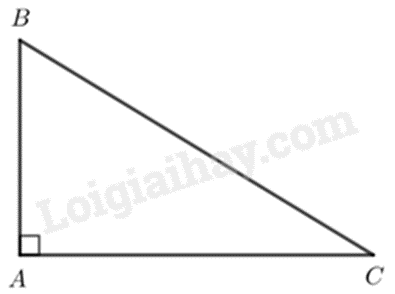
Xét tam giác ABC có \(A{B^2} + A{C^2} = {5^2} + {12^2} = 169 = {13^2} = B{C^2}\) nên tam giác ABC vuông tại A.
Tỉ số lượng giác cosB là: \(\cos B = \frac{{AB}}{{BC}} = \frac{5}{{13}}\).
Đáp án B.
Giá trị của biểu thức \({\sin ^2}25^\circ + {\cos ^2}25^\circ \) là
-
A.
0.
-
B.
1.
-
C.
2.
-
D.
3.
Đáp án : B
Sử dụng máy tính cầm tay để tính.
Bấm máy tính, ta được: \({\sin ^2}25^\circ + {\cos ^2}25^\circ = 1\).
Đáp án B.
Cho tam giác ABC vuông tại A có BC = 10cm, \(\widehat C = 30^\circ \). Độ dài cạnh AB là:
-
A.
5,5cm.
-
B.
5cm.
-
C.
\(5\sqrt 3 \)cm.
-
D.
\(5\sqrt 2 \)cm.
Đáp án : B
Trong tam giác vuông, mỗi cạnh góc vuông bằng cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề.
Cạnh góc vuông = (cạnh huyền ) × (sin góc đối)
= (cạnh huyền ) × (cosin góc kề)
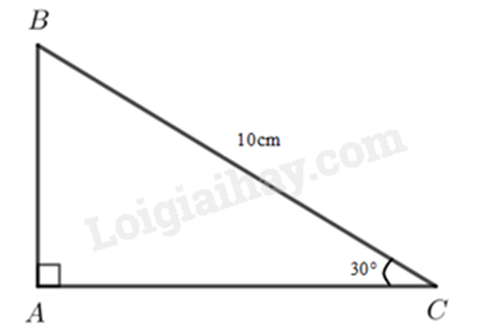
Xét tam giác vuông ABC, ta có:
\(AB = BC.\sin C = 10.\sin 30^\circ = 5\left( {cm} \right)\).
Đáp án B.
1. a) Đưa phương trình về phương trình tích để giải.
b) Tìm điều kiện xác định, quy đồng mẫu và giải phương trình tìm được. Sau đó kiểm tra điều kiện của các nghiệm tìm được.
c, d) Dựa vào cách giải bất phương trình bậc nhất một ẩn và phương trình đưa về dạng bất phương tình bậc nhất một ẩn.
2. Sử dụng phương pháp cộng đại số để giải hệ phương trình.
1. Giải các phương trình và bất phương trình sau:
a) \({x^2} + 2x - 3 = 0\)
\(\begin{array}{l}{x^2} - x + 3x - 3 = 0\\\left( {{x^2} - x} \right) + \left( {3x - 3} \right) = 0\\x\left( {x - 1} \right) + 3\left( {x - 1} \right) = 0\\\left( {x + 3} \right)\left( {x - 1} \right) = 0\end{array}\)
+) \(x + 3 = 0\) suy ra \(x = - 3\).
+) \(x - 1 = 0\) suy ra \(x = 1\).
Vậy phương trình có hai nghiệm \(x = - 3;x = 1\).
b) \(\frac{{2x + 1}}{{2x}} - \frac{x}{{x + 2}} = 0\)
ĐKXĐ: \(2x \ne 0\) và \(x + 2 \ne 0\)
hay \(x \ne 0\) và \(x \ne - 2\).
Ta có: \(\frac{{2x + 1}}{{2x}} - \frac{x}{{x + 2}} = 0\)
\(\begin{array}{l}\frac{{\left( {2x + 1} \right)\left( {x + 2} \right)}}{{2x\left( {x + 2} \right)}} - \frac{{x.2x}}{{2x\left( {x + 2} \right)}} = 0\\\left( {2x + 1} \right)\left( {x + 2} \right) - x.2x = 0\\2{x^2} + x + 4x + 2 - 2{x^2} = 0\\5x + 2 = 0\\x = \frac{{ - 2}}{5}\left( {TM} \right)\end{array}\)
Vậy nghiệm của phương trình là \(x = \frac{{ - 2}}{5}\).
c) \(3x - 5 < 2x + 2\)
\(\begin{array}{l}3x - 2x < 2 + 5\\x < 7\end{array}\)
Vậy nghiệm của bất phương trình là \(x < 7\).
d) \(\frac{{2x + 3}}{2} \ge \frac{{1 - x}}{3} + 1\)
\(\begin{array}{l}\frac{{3\left( {2x + 3} \right)}}{{2.3}} \ge \frac{{2\left( {1 - x} \right)}}{{3.2}} + \frac{6}{6}\\3\left( {2x + 3} \right) \ge 2\left( {1 - x} \right) + 6\\6x + 9 \ge 2 - 2x + 6\\6x + 2x \ge 2 + 6 - 9\\8x \ge - 1\\x \ge \frac{{ - 1}}{8}\end{array}\)
Vậy nghiệm của bất phương trình là \(x \ge \frac{{ - 1}}{8}\).
2. Giải hệ phương trình \(\left\{ \begin{array}{l}2x - y = 4\\x + 2y = - 3\end{array} \right.\)
Ta có: \(\left\{ \begin{array}{l}2x - y = 4\\x + 2y = - 3\end{array} \right.\)
Nhân cả hai vế của phương trình \(2x - y = 4\) với 2, ta được hệ phương trình \(\left\{ \begin{array}{l}4x - 2y = 8\\x + 2y = - 3\end{array} \right.\).
Cộng hai vế của hai phương trình trong hệ mới, ta được \(5x = 5\) suy ra \(x = 1\).
Thế vào phương trình \(2x - y = 4\), ta được \(2.1 - y = 4\) suy ra \(y = - 2\).
Vậy nghiệm của hệ phương trình là \(\left( {x;y} \right) = \left( {1; - 2} \right)\).
Gọi số khẩu trang khu phố cô Mai may được là \(x\) (khẩu trang, \(x \in {\mathbb{N}^*},x < 720\))
Số khẩu trang khu phố cô Lan may được là \(y\) (khẩu trang, \(y \in {\mathbb{N}^*},y < 720\))
Biểu diễn hệ phương trình theo x và y.
Giải hệ phương trình để tìm x và y.
Gọi số khẩu trang khu phố cô Mai may được là \(x\) (khẩu trang, \(x \in {\mathbb{N}^*},x < 720\))
Số khẩu trang khu phố cô Lan may được là \(y\) (khẩu trang, \(y \in {\mathbb{N}^*},y < 720\))
Vì tổng số khẩu trang của hai khu phố là 720 chiếc:
\(x + y = 720\) (1)
Lần thứ hai khu phố cô Mai may được vượt mức 15%, nên số khẩu trang khu phố cô Mai may được là:
\(x + 0,15x = 1,15x\) (khẩu trang)
Lần thứ hai khu phố cô Lan may được vượt mức 12%, nên số khẩu trang khu phố cô Lan may được là:
\(y + 0,12y = 1,12y\) (khẩu trang)
Vì trong hai lần cả hai khu phố đã may được 819 cái khẩu trang:
\(1,15x + 1,12y = 819\) (2)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{ {\begin{array}{*{20}{l}}{x + y = 720}\\{1,15x + 1,12y = 819}\end{array}} \right.\)
Từ phương trình (1) ta có: \(x = 720 - y\)
Thay \(x = 720 - y\) vào phương trình thứ hai:
\(1,15(720 - y) + 1,12y = 819\)
\(1,15.720 - 1,15y + 1,12y = 819\)
\(828 - 1,15y + 1,12y = 819\)
\( - 0,03y = - 9\)
\(y = 300\)
Thay \(y = 300\) vào phương trình \(x + y = 720\), ta được:
\(x + 300 = 720\)
\(x = 420\)
Vậy lần thứ hai khu phố cô Mai may được 1,15.420 = 483 chiếc khẩu trang; khu phố cô Lan may được 1,12.300 = 336 chiếc khẩu trang.
Gọi số bánh trôi có thể nặn là x.
Biểu diễn bất phương trình bậc nhất một ẩn theo x dựa vào dữ kiện đề bài.
Giải bất phương trình để tìm số bánh trôi mà bác An nặn được nhiều nhất.
Gọi số bánh trôi bác An có thể nặn là \(x\) (chiếc), \(x \in {\mathbb{N}^*}\).
Đổi 1 giờ 30 phút = 90 phút.
Vì bánh trôi cần 1 phút để nặn xong 1 chiếc, bánh chay cần 2 phút để nặn xong 1 chiếc, mà trong 1 giờ 30 phút bác An nặn được 15 chiếc bánh chay nên ta có bất phương trình:
\(\begin{array}{l}1.x + 2.15 \le 90\\x + 30 \le 90\\x \le 60\end{array}\)
Vậy bác An có thể nặn nhiều nhất 60 chiếc bánh trôi.
a) Vận dụng các kiến thức về hệ thức lượng và định lí Pythagore trong tam giác vuông để giải tam giác.
b) Chứng minh AHBE là hình chữ nhật nên AB = HE.
Chứng minh $\Delta ABK\backsim \Delta BCK\left( g.g \right)$ suy ra \(A{B^2} = AK.AC\).
Từ đó chứng minh được \(H{E^2} = AK.AC\).
c) Chứng minh $\Delta ABC\backsim \Delta NMC\left( g.g \right)$ suy ra \(\frac{{CN}}{{AC}} = \frac{{CM}}{{BC}}\).
Chứng minh $\Delta BMC\backsim \Delta ANC\left( c.g.c \right)$ suy ra \(\frac{{BM}}{{BC}} = \frac{{AN}}{{AC}}\).
Biểu diễn \(\cos C\) trong tam giác vuông ABC. Từ đó suy ra điều phải chứng minh.
a) Xét tam giác ABC vuông tại A, số đo góc B là:
\(\widehat B = 90^\circ - \widehat C = 90^\circ - 30^\circ = 60^\circ \).
Áp dụng tỉ số lượng giác trong tam giác vuông vào tam giác ABC, ta có: \(\tan B = \frac{{AC}}{{AB}}\)
suy ra \(AC = AB.\tan B = 12.\tan 60^\circ = 12\sqrt 3 \left( {cm} \right)\)
Áp dụng định lí Pythagore vào tam giác vuông, ta có:
\(BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {{{12}^2} + {{\left( {12\sqrt 3 } \right)}^2}} = 24\left( {cm} \right)\)
Vậy \(\widehat B = 60^\circ ,AC = 12\sqrt 3 cm,BC = 24cm\).
b) Xét tứ giác AHBE có: \(\widehat H = \widehat B = \widehat E\left( { = 90^\circ } \right)\) nên tứ giác AHBE là hình chữ nhật, suy ra AB = HE. (1)
Xét tam giác ABK và tam giác ACB có:
\(\widehat {BAK} = \widehat {CAB}\left( { = 90^\circ } \right)\)
\(\widehat {AKB} = \widehat {ABC}\) (cùng phụ với \(\widehat C\))
suy ra $\Delta ABK\backsim \Delta BCK\left( g.g \right)$
Do đó \(\frac{{AB}}{{AK}} = \frac{{AC}}{{AB}}\) nên \(A{B^2} = AK.AC\). (2)
Từ (1) và (2) suy ra \(H{E^2} = AK.AC\) (đpcm)
c) Xét tam giác ABC và tam giác NMC có:
\(\widehat A = \widehat N\left( { = 90^\circ } \right)\)
\(\widehat C\) chung
Suy ra $\Delta ABC\backsim \Delta NMC\left( g.g \right)$.
Do đó \(\frac{{CN}}{{AC}} = \frac{{CM}}{{BC}}\).
Xét tam giác BMC và tam giác ANC có:
\(\frac{{CN}}{{AC}} = \frac{{CM}}{{BC}}\) (cmt)
\(\widehat C\) chung
Suy ra $\Delta BMC\backsim \Delta ANC\left( c.g.c \right)$.
Do đó \(\frac{{BM}}{{BC}} = \frac{{AN}}{{AC}}\) hay \(AN = BM.\frac{{AC}}{{BC}}\).
Trong tam giác vuông ABC, ta có: \(\cos C = \frac{{AC}}{{BC}}\).
Từ đó suy ra \(AN = BM.\frac{{AC}}{{BC}} = BM.\cos C\). (đpcm)
Vẽ \(AK \bot BC\) tại K, \(AH \bot DC\) tại H, chứng minh \(AK = CH,AH = CK\)
Biểu diễn AK, BK theo AB và \(\widehat {ABK}\).
Từ đó biểu diễn AH, DH.
Áp dụng định lí Pythagore vào tam giác vuông ADH để tính AD.
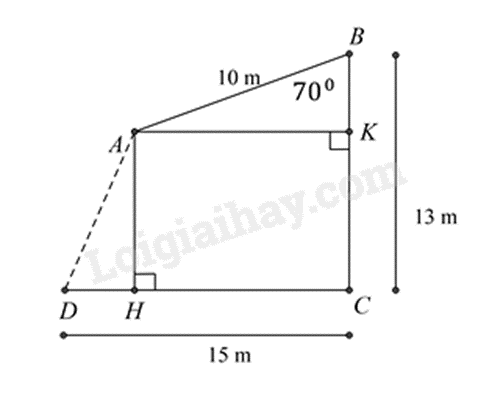
Vẽ \(AK \bot BC\) tại K, \(AH \bot DC\) tại H, khi đó tứ giác \(AKCH\) là hình chữ nhật.
Suy ra \(AK = CH,AH = CK\)
Trong tam giác vuông \(AKB\) vuông tại \(K\) có \(AB = 10cm\), \(\widehat {ABK} = 70^\circ \)
+) \(AK = AB.\sin 70^\circ = 10.\sin 70^\circ \)
Suy ra \(AK = CH = 10.\sin 70^\circ \)
Hay \(DH = CD - HC = 15 - 10.\sin 70^\circ \)
+) \(BK = AB.\cos 70^\circ = 10.\cos 70^\circ \)
Suy ra \(CK = CB - BK = 13 - 10.\cos {70^0}\)
Hay \(AH = CK = 13 - 10.\cos 70^\circ \)
Theo định lí Pythagore trong tam giác vuông \(ADH\), ta có:
\(AD = \sqrt {A{H^2} + D{H^2}} = \sqrt {{{\left( {13 - 10.\cos 70^\circ } \right)}^2} + {{\left( {15 - 10.\sin 70^\circ } \right)}^2}} \approx 11,1{\rm{ }}m\)
Phần I. Câu hỏi trắc nghiệm nhiều phương án lựa chọn Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Phần I. Câu hỏi trắc nghiệm nhiều phương án lựa chọn Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau: Câu 1: Nghiệm của phương trình \(x + 2y = 0\) là:
Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau: Câu 1: Trong các phương trình sau, phương trình nào không phải là phương trình bậc nhất hai ẩn?
