Đề thi học kì 2 Toán 9 - Đề số 3
Phần I. Câu hỏi trắc nghiệm nhiều phương án lựa chọn (3 điểm) Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Đề bài
Xác định hệ số a của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\), biết đồ thị của hàm số đi qua điểm A(1;1).
-
A.
1.
-
B.
2.
-
C.
3.
-
D.
4.
Giá trị của tham số \(m\) để phương trình \({x^2} + 2x - 3m = 0\;\) có hai nghiệm phân biệt.
-
A.
\(m < \frac{1}{3}.\)
-
B.
\(m > \frac{1}{3}.\)
-
C.
\(m < - \frac{1}{3}.\)
-
D.
\(m > - \frac{1}{3}.\)
Cho phương trình \({x^2} - 14x + 33 = 0\). Không giải phương trình, hãy tính tổng và tích các nghiệm, hãy chọn câu đúng:
-
A.
\({x_1} + {x_2} = 33;\;{x_1}{x_2} = 14\).
-
B.
\({x_1} + {x_2} = 14;\;{x_1}{x_2} = 33\).
-
C.
\({x_1} + {x_2} = 11;\;{x_1}{x_2} = 3\).
-
D.
\({x_1} + {x_2} = 14;\;{x_1}{x_2} = - 33\).
Một trường trung học tiến hành khảo sát điểm kiểm tra toán của 200 học sinh lớp 9. Kết quả được thống kê theo bảng và biểu đồ tần số tương đối ghép nhóm dưới đây:
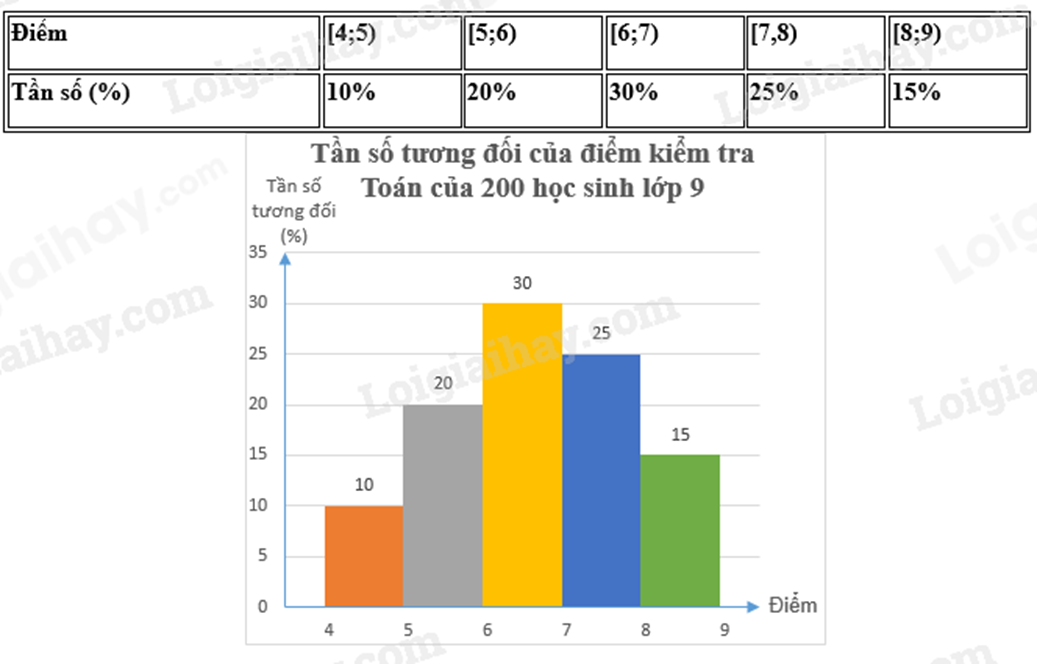
Hỏi có bao nhiêu học sinh đạt điểm từ 6 đến dưới 8?
-
A.
60.
-
B.
100.
-
C.
110.
-
D.
80.
Bạn Lan gieo một con xúc xắc liên tiếp 2 lần. Số phần tử của không gian mẫu là
-
A.
\(2\).
-
B.
\(4\).
-
C.
\(6\).
-
D.
\(36\).
Cho bán kính của đường tròn nội tiếp tam giác đều là \(\frac{{\sqrt 3 }}{2}cm\). Độ dài cạnh của tam giác đều đó là:
-
A.
\(\frac{3}{2}cm\).
-
B.
\(\frac{{3\sqrt 3 }}{2}cm\).
-
C.
\(3cm\).
-
D.
\(\sqrt 3 cm\).
Trong các hình sau, hình nào sau đây không nội tiếp được đường tròn?
-
A.
Hình vuông.
-
B.
Hình chữ nhật.
-
C.
Hình thoi có một góc nhọn.
-
D.
Hình thang cân.
Cho đa giác đều \(11\) cạnh có độ dài mỗi cạnh là \(5cm\). Tính chu vi đa giác.
-
A.
\(45cm\).
-
B.
\(50cm\).
-
C.
\(60cm\).
-
D.
\(55cm\).
Trong các hình dưới đây hình nào vẽ hai điểm A và B thỏa mãn phép quay thuận chiều \(60^\circ \) biến điểm A thành điểm B.
-
A.
Hình 1.
-
B.
Hình 2.
-
C.
Hình 3.
-
D.
Hình 4.
Cho hình trụ có bán kính đáy R = 8cm và diện tích toàn phần là \(564\pi c{m^2}\). Chiều cao của hình trụ là:
-
A.
27cm.
-
B.
27,25cm.
-
C.
25cm.
-
D.
25,27cm.
Khi quay một hình tam giác vuông một vòng xung quanh đường thẳng cố định chứa một cạnh góc vuông ta được:
-
A.
Hình nón.
-
B.
Hình lập phương.
-
C.
Hình cầu.
-
D.
Hình trụ.
Tính diện tích mặt cầu của quả địa cầu trong hình vẽ sau, biết đường kính quả địa cầu \(d = 30cm\) (quả địa cầu có dạng một hình cầu).
-
A.
\(60\pi \) \(\left( {c{m^2}} \right)\).
-
B.
\(450\pi \) \(\left( {c{m^2}} \right)\).
-
C.
\(900\pi \) \(\left( {c{m^2}} \right)\).
-
D.
\(300\pi \) \(\left( {c{m^2}} \right)\).
Một tổ máy trộn bê tông phải sản xuất \(450{m^3}\) bê tông cho một đập thuỷ lợi trong một thời gian quy định. Nhờ tăng năng suất mỗi ngày \(4,5{m^3}\;\)nên \(4\)ngày trước thời hạn quy định tổ đã sản xuất được \(96\% \) công việc.
a) \(4\) ngày trước thời hạn quy định tổ đã sản xuất được \(432{m^3}\) bê tông.
b) Số ngày đổ bê tông theo quy định là \(20\) ngày.
c) Lượng bê tông thực tế sản xuất được trong một ngày là \(22,5{\rm{ }}{m^3}\).
d) Theo năng suất thực tế thì cần 16 ngày để hoàn thành \(450{m^3}\) bê tông.
Một cái bồn chứa dầu gồm hai bán cầu và một hình trụ (như hình vẽ) (lấy \(\pi \approx 3,14\))
a) Bán kính của bán cầu bằng \(1,8\) m.
b) Diện tích xung quanh của bồn chứa bằng \(8,1\) \({m^2}\).
c) Thể tích của bồn chứa là \(12,26{m^3}\).
d) Lượng dầu tối đa có thể chứa được trong bồn là 3110,4 kg. biết khối lượng riêng của dầu hỏa là \(800kg/{m^3}\).
Biết phương trình \(2{x^2}\; + {\rm{ }}ax{\rm{ }} - 3{a^2}{\rm{ = }}0\) có một nghiệm bằng \( - 3\). Tính tổng các giá trị a.
Đáp án:
Một lớp học gồm 40 học sinh được khảo sát về chiều cao và đưa ra bảng tần số ghép nhóm dưới đây:
Tần số tương đối ghép nhóm của nhóm \([170;180)\) là bao nhiêu %?
Đáp án:
Bạn An giải một đề thi gồm có ba bài được đánh số 1; 2; 3. An được chọn lần lượt các bài để giải theo một thứ tự ngẫu nhiên. Tính xác suất của biến cố A: “An giải bài 1 trước bài 3” (viết dưới dạng số thập phân)
Đáp án:
Cho lục giác đều ABCDEF nội tiếp đường tròn (O). Phép quay thuận chiều \(\alpha ^\circ \) tâm O biến điểm A thành điểm C. Giá trị của \(\alpha \) là
Đáp án:
Lời giải và đáp án
Xác định hệ số a của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\), biết đồ thị của hàm số đi qua điểm A(1;1).
-
A.
1.
-
B.
2.
-
C.
3.
-
D.
4.
Đáp án : A
Thay toạ độ điểm A vào hàm số để tìm a.
Vì đồ thị của hàm số đi qua điểm A(1;1) nên thay \(x = 1;y = 1\), ta được:
\(1 = a{.1^2}\) suy ra a = 1.
Đáp án A
Giá trị của tham số \(m\) để phương trình \({x^2} + 2x - 3m = 0\;\) có hai nghiệm phân biệt.
-
A.
\(m < \frac{1}{3}.\)
-
B.
\(m > \frac{1}{3}.\)
-
C.
\(m < - \frac{1}{3}.\)
-
D.
\(m > - \frac{1}{3}.\)
Đáp án : D
Tính \(\Delta \) hoặc \(\Delta '\) của phương trình.
Để phương trình có hai nghiệm phân biệt thì \(\Delta > 0\) hoặc \(\Delta ' > 0\).
Giải bất phương trình để tìm m.
Phương trình \({x^2} + 2x - 3m = 0\;\) có hệ số \(a = 1;b' = \frac{2}{2} = 1;c = - 3m\) nên ta có hệ thức:
\(\Delta ' = {1^2} - 1.\left( { - 3m} \right) = 1 + 3m\).
Để phương trình có hai nghiệm phân biệt thì \(1 + 3m > 0\).
Giải bất phương trình:
\(\begin{array}{l}1 + 3m > 0\\3m > - 1\\m > - \frac{1}{3}\end{array}\)
Vậy \(m > - \frac{1}{3}\) thì phương trình \({x^2} + 2x - 3m = 0\;\) có hai nghiệm phân biệt.
Đáp án D
Cho phương trình \({x^2} - 14x + 33 = 0\). Không giải phương trình, hãy tính tổng và tích các nghiệm, hãy chọn câu đúng:
-
A.
\({x_1} + {x_2} = 33;\;{x_1}{x_2} = 14\).
-
B.
\({x_1} + {x_2} = 14;\;{x_1}{x_2} = 33\).
-
C.
\({x_1} + {x_2} = 11;\;{x_1}{x_2} = 3\).
-
D.
\({x_1} + {x_2} = 14;\;{x_1}{x_2} = - 33\).
Đáp án : B
Kiểm tra xem phương trình có nghiệm hay không.
Nếu có, sử dụng định lí Viète để tính tổng và tích các nghiệm: \(\left\{ \begin{array}{l}{x_1} + {x_2} = \frac{{ - b}}{a}\\{x_1}.{x_2} = \frac{c}{a}\end{array} \right.\).
Ta có: \(\Delta = {\left( { - 14} \right)^2} - 4.33 = 64 > 0\) nên phương trình có hai nghiệm phân biệt \({x_1},{x_2}\).
Áp dụng định lí Viète, ta có:
\(\left\{ \begin{array}{l}{x_1} + {x_2} = \frac{{ - b}}{a} = \frac{{14}}{1} = 14\\{x_1}.{x_2} = \frac{c}{a} = \frac{{33}}{1} = 33\end{array} \right.\).
Đáp án B
Một trường trung học tiến hành khảo sát điểm kiểm tra toán của 200 học sinh lớp 9. Kết quả được thống kê theo bảng và biểu đồ tần số tương đối ghép nhóm dưới đây:
Hỏi có bao nhiêu học sinh đạt điểm từ 6 đến dưới 8?
-
A.
60.
-
B.
100.
-
C.
110.
-
D.
80.
Đáp án : C
Tính tổng tần số tương đối các học sinh từ 6 đến dưới 8 điểm.
Từ đó tính số học sinh từ 6 đến dưới 8 điểm dựa vào công thức tính tỉ số phần trăm của một số.
Tổng tần số tương đối các học sinh từ 6 đến dưới 8 điểm là: 30 + 25 = 55(%)
Số học sinh từ 6 đến dưới 8 điểm là: \(\frac{{200.55}}{{100}} = 110\) (học sinh)
Đáp án C
Bạn Lan gieo một con xúc xắc liên tiếp 2 lần. Số phần tử của không gian mẫu là
-
A.
\(2\).
-
B.
\(4\).
-
C.
\(6\).
-
D.
\(36\).
Đáp án : D
Xác định các phần tử của không gian mẫu.
Không gian mẫu của phép thử là:
\(\Omega = \left\{ \begin{array}{l}\left( {1;1} \right),\left( {1;2} \right),\left( {1;3} \right),\left( {1;4} \right),\left( {1;5} \right),\left( {1;6} \right),\\\left( {2;1} \right),\left( {2;2} \right),\left( {2;3} \right),\left( {2;4} \right),\left( {2;5} \right),\left( {2;6} \right),\\\left( {3;1} \right),\left( {3;2} \right),\left( {3;3} \right),\left( {3;4} \right),\left( {3;5} \right),\left( {3;6} \right),\\\left( {4;1} \right),\left( {4;2} \right),\left( {4;3} \right),\left( {4;4} \right),\left( {4;5} \right),\left( {4;6} \right),\\\left( {5;1} \right),\left( {5;2} \right),\left( {5;3} \right),\left( {5;4} \right),\left( {5;5} \right),\left( {5;6} \right),\\\left( {6;1} \right),\left( {6;2} \right),\left( {6;3} \right),\left( {6;4} \right),\left( {6;5} \right),\left( {6;6} \right)\end{array} \right\}\).
Số phần tử của không gian mẫu là 36.
Đáp án D
Cho bán kính của đường tròn nội tiếp tam giác đều là \(\frac{{\sqrt 3 }}{2}cm\). Độ dài cạnh của tam giác đều đó là:
-
A.
\(\frac{3}{2}cm\).
-
B.
\(\frac{{3\sqrt 3 }}{2}cm\).
-
C.
\(3cm\).
-
D.
\(\sqrt 3 cm\).
Đáp án : C
Bán kính đường của tròn nội tiếp tam giác đều cạnh a là \(\frac{{a\sqrt 3 }}{6}\). Từ đó ta tính độ dài cạnh theo bán kính.
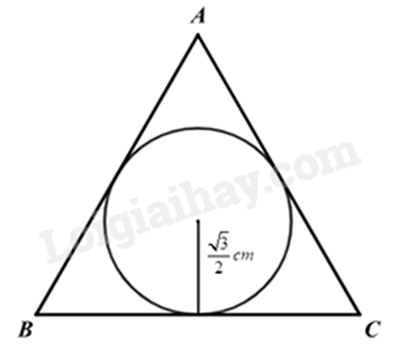
Giả sử cạnh của tam giác đều là a (cm) thì bán kính của đường tròn nội tiếp tam giác đều là \(\frac{{a\sqrt 3 }}{6}\) (cm).
Do đó ta có: \(\frac{{a\sqrt 3 }}{6} = \frac{{\sqrt 3 }}{2}\) suy ra \(a = \frac{{\sqrt 3 }}{2}:\frac{{\sqrt 3 }}{6} = 3\left( {cm} \right)\).
Đáp án C
Trong các hình sau, hình nào sau đây không nội tiếp được đường tròn?
-
A.
Hình vuông.
-
B.
Hình chữ nhật.
-
C.
Hình thoi có một góc nhọn.
-
D.
Hình thang cân.
Đáp án : C
Dựa vào tính chất tổng hai góc đối bằng \(180^\circ \).
Trong các hình trên, chỉ có hình thoi có một góc nhọn là không nội tiếp được đường tròn vì hình thoi hai cặp góc đối bằng nhau.
Nếu hình thoi có một góc nhọn thì góc đối của nó cũng là góc nhọn nên tổng của chúng không thể bằng \(180^\circ \) nên không thoả mãn tính chất của đường tròn nội tiếp.
Đáp án C
Cho đa giác đều \(11\) cạnh có độ dài mỗi cạnh là \(5cm\). Tính chu vi đa giác.
-
A.
\(45cm\).
-
B.
\(50cm\).
-
C.
\(60cm\).
-
D.
\(55cm\).
Đáp án : D
Chu vi của đa giác bằng tổng độ dài các cạnh của đa giác đó.
Vì đa giác là đa giác đều nên chu vi của đa giác là: \(5.11 = 55\left( {cm} \right)\)
Đáp án D
Trong các hình dưới đây hình nào vẽ hai điểm A và B thỏa mãn phép quay thuận chiều \(60^\circ \) biến điểm A thành điểm B.
-
A.
Hình 1.
-
B.
Hình 2.
-
C.
Hình 3.
-
D.
Hình 4.
Đáp án : D
Phép quay thuận chiều \(\alpha ^\circ \) tâm O biến điểm A thành điểm B.
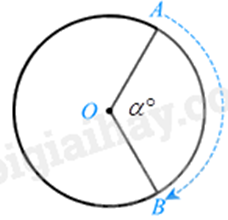
Phép quay thuận chiều \(60^\circ \) tâm O biến điểm A thành điểm B là:
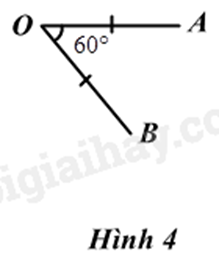
Đáp án D
Cho hình trụ có bán kính đáy R = 8cm và diện tích toàn phần là \(564\pi c{m^2}\). Chiều cao của hình trụ là:
-
A.
27cm.
-
B.
27,25cm.
-
C.
25cm.
-
D.
25,27cm.
Đáp án : B
Công thức tính diện tích toàn phần của hình trụ:
${{S}_{tp}}={{S}_{xq}}+{{S}_{2 \text{đáy}}}=2\pi Rh+2\pi {{R}^{2}}$ suy ra chiều cao của hình trụ.
Ta có diện tích toàn phần của hình trụ là:
${{S}_{tp}}={{S}_{xq}}+{{S}_{2 \text{đáy}}}=564\pi $
\(\begin{array}{l}2\pi .8.h + 2\pi {.8^2} = 564\pi \\16\pi h + 128\pi = 564\pi \\16\pi h = 436\pi \\h = \frac{{436\pi }}{{16\pi }} = 27,25\end{array}\)
Vậy \(h = 27,25cm\).
Đáp án B
Khi quay một hình tam giác vuông một vòng xung quanh đường thẳng cố định chứa một cạnh góc vuông ta được:
-
A.
Hình nón.
-
B.
Hình lập phương.
-
C.
Hình cầu.
-
D.
Hình trụ.
Đáp án : A
Dựa vào kiến thức về hình nón.
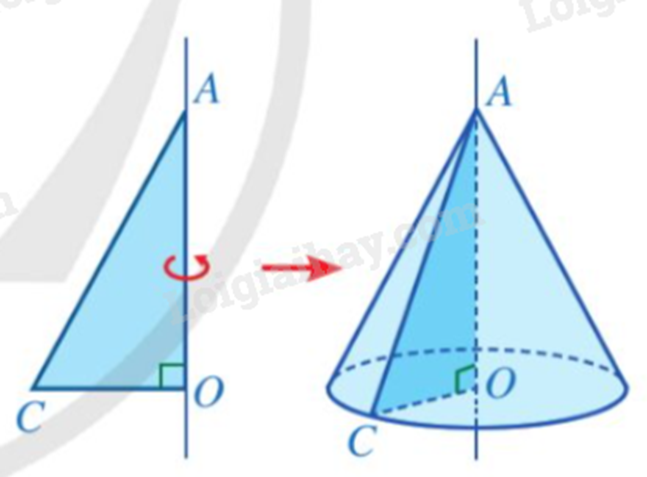
Hình nón là hình được tạo ra khi quay một hình tam giác vuông một vòng xung quanh đường thẳng cố định chứa một cạnh góc vuông của tam giác đó.
Đáp án A
Tính diện tích mặt cầu của quả địa cầu trong hình vẽ sau, biết đường kính quả địa cầu \(d = 30cm\) (quả địa cầu có dạng một hình cầu).
-
A.
\(60\pi \) \(\left( {c{m^2}} \right)\).
-
B.
\(450\pi \) \(\left( {c{m^2}} \right)\).
-
C.
\(900\pi \) \(\left( {c{m^2}} \right)\).
-
D.
\(300\pi \) \(\left( {c{m^2}} \right)\).
Đáp án : C
Giả sử quả địa cầu là một hình cầu tâm O bán kính r.
Sử dụng công thức tính diện tích mặt cầu bán kính r: \(S = 4\pi {r^2}\). Đối công thức sử dụng đường kính của hình cầu và tính.
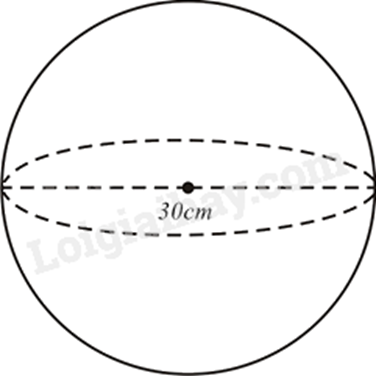
Giả sử quả địa cầu là một hình cầu tâm O bán kính r.
Diện tích mặt cầu có tâm O bán kính r là: \(S = 4\pi {r^2}\) hay \(S = \pi {d^2}\) (với \(d = 2r\) là đường kính của hình cầu)
Do đó \(S = \pi {.30^2} = 900\pi \left( {c{m^2}} \right)\)
Đáp án C
Một tổ máy trộn bê tông phải sản xuất \(450{m^3}\) bê tông cho một đập thuỷ lợi trong một thời gian quy định. Nhờ tăng năng suất mỗi ngày \(4,5{m^3}\;\)nên \(4\)ngày trước thời hạn quy định tổ đã sản xuất được \(96\% \) công việc.
a) \(4\) ngày trước thời hạn quy định tổ đã sản xuất được \(432{m^3}\) bê tông.
b) Số ngày đổ bê tông theo quy định là \(20\) ngày.
c) Lượng bê tông thực tế sản xuất được trong một ngày là \(22,5{\rm{ }}{m^3}\).
d) Theo năng suất thực tế thì cần 16 ngày để hoàn thành \(450{m^3}\) bê tông.
a) \(4\) ngày trước thời hạn quy định tổ đã sản xuất được \(432{m^3}\) bê tông.
b) Số ngày đổ bê tông theo quy định là \(20\) ngày.
c) Lượng bê tông thực tế sản xuất được trong một ngày là \(22,5{\rm{ }}{m^3}\).
d) Theo năng suất thực tế thì cần 16 ngày để hoàn thành \(450{m^3}\) bê tông.
a) Sử dụng công thức tính m% của một số a: \(m\% .a\)
b) Gọi số ngày đổ bê tông theo quy định là \(x\)(ngày)
Biểu diễn lượng bê tông sản xuất mỗi ngày theo quy định và thực tế theo \(x\).
Vì \(4\) ngày trước thời hạn quy định tổ sản xuất được \(96\% \) công việc nên ta có phương trình để tìm số ngày đổ bê tông theo quy định.
Giải phương trình và kiểm tra lại nghiệm.
c) Tính lượng bê tông thực tế sản xuất được theo công thức biểu diễn.
d) Tính năng suất = lượng bê tông : số ngày.
a) Đúng
Thực tế, \(4\) ngày trước thời hạn quy định tổ đã sản xuất được: \(96\% .{\rm{ }}450 = 432\) ( \({m^3}\) bê tông)
b) Đúng
Gọi số ngày đổ bê tông theo quy định là: \(x\)(ngày)
Số lượng bê tông cần đổ trong một ngày \(\frac{{450}}{x}\left( {{m^3}} \right)\)
Số lượng bê tông thực tế sản xuất được trong một ngày là: \(\frac{{450}}{x} + 4,5\left( {{m^3}} \right)\)
Vì \(4\) ngày trước thời hạn quy định tổ sản xuất được \(96\% \) công việc nên ta có phương trình:
\(\begin{array}{l}\left( {\frac{{450}}{x} + 4,5} \right)\left( {x - 4} \right) = 432\\450 + 4,5x - \frac{{1800}}{x} - 18 = 432\\4,5{x^2} = 1800\\{x^2} = 400\end{array}\)
Suy ra \({x_1} = - 20\) (loại); \({x_2} = 20\) (thỏa mãn)
Vậy số ngày đổ bê tông theo quy định là \(20\) ngày.
c) Sai
Lượng bê tông thực tế sản xuất được trong một ngày là: \(\frac{{450}}{{20}} + 4,5 = 27\left( {{m^3}} \right)\)
d) Sai
Theo năng suất thực tế thì cần \(450:27 = 16,\left( 6 \right) \approx \;17\) ngày để hoàn thành \(450{m^3}\) bê tông.
Đáp án: ĐĐSS
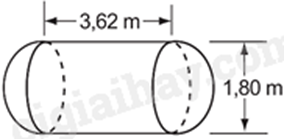
Một cái bồn chứa dầu gồm hai bán cầu và một hình trụ (như hình vẽ) (lấy \(\pi \approx 3,14\))
a) Bán kính của bán cầu bằng \(1,8\) m.
b) Diện tích xung quanh của bồn chứa bằng \(8,1\) \({m^2}\).
c) Thể tích của bồn chứa là \(12,26{m^3}\).
d) Lượng dầu tối đa có thể chứa được trong bồn là 3110,4 kg. biết khối lượng riêng của dầu hỏa là \(800kg/{m^3}\).
a) Bán kính của bán cầu bằng \(1,8\) m.
b) Diện tích xung quanh của bồn chứa bằng \(8,1\) \({m^2}\).
c) Thể tích của bồn chứa là \(12,26{m^3}\).
d) Lượng dầu tối đa có thể chứa được trong bồn là 3110,4 kg. biết khối lượng riêng của dầu hỏa là \(800kg/{m^3}\).
a) Từ đường kính tính bán kính của bán cầu.
b) Diện tích xung quanh của bồn chứa = diện tích xung quanh hình trụ và diện tích hai nửa mặt cầu (diện tích một mặt cầu): \({S_{xq}}(T) = 2\pi Rh;S(C) = 4\pi {R^2}\)
c) Thể tích của bồn chứa = thể tích hình trụ và thể tích mặt cầu (tổng thể tích hai nửa mặt cầu):
\({V_T} = \pi {R^2}h;{V_C} = \frac{4}{3}\pi {R^3}\)
d) Lượng dầu tối đa bằng = thể tích dầu . khối lượng riêng của dầu hỏa: \(\left( {m = D.V} \right)\).
a) Sai
Bán kính bán cầu bằng \(\frac{{1,8}}{2} = 0,9\)m.
b) Sai
Diện tích xung quanh bồn chứa bằng:
\({S_{xq}} = 4\pi .0,{9^2} + 2\pi .0,9.3,62 \approx 30,6\) \(\left( {{m^2}} \right)\)
c) Đúng
Thể tích bồn chứa là:
\(V = \pi .0,{9^2}.3,62 + \frac{4}{3}\pi .0,{9^3} \approx 12,26\left( {{m^3}} \right)\)
d) Sai
Khối lượng dầu hỏa là:
\(m = D.V = 800.12,26 = 9808\) (kg)
Đáp án: SSĐS
Biết phương trình \(2{x^2}\; + {\rm{ }}ax{\rm{ }} - 3{a^2}{\rm{ = }}0\) có một nghiệm bằng \( - 3\). Tính tổng các giá trị a.
Đáp án:
Đáp án:
Thay \(x = - 3\) vào phương trình. Giải phương trình bậc hai ẩn a để tìm a.
Thay \(x = - 3\) vào phương trình, ta được:
\(\begin{array}{l}2.{\left( { - 3} \right)^2}\; + {\rm{ }}a\left( { - 3} \right){\rm{ }} - 3{a^2}{\rm{ = }}0\\18 - 3a - 3{a^2} = 0\\{a^2} + a - 6 = 0\end{array}\)
Ta có: \(\Delta = {1^2} - 4.\left( { - 6} \right) = 25 > 0\) nên phương trình có hai nghiệm \({a_1} = \frac{{ - 1 - \sqrt {25} }}{2} = - 3;{a_2} = \frac{{ - 1 + \sqrt {25} }}{2} = 2\)
Suy ra tổng các giá trị của a là: -3 + 2 = -1.
Đáp án: -1
Một lớp học gồm 40 học sinh được khảo sát về chiều cao và đưa ra bảng tần số ghép nhóm dưới đây:
Tần số tương đối ghép nhóm của nhóm \([170;180)\) là bao nhiêu %?
Đáp án:
Đáp án:
Từ bảng tần số ghép nhóm, xác định tần số của nhóm [170; 180).
Tính tần số tương đối ghép nhóm của nhóm: tần số : tổng tần số.100%
Từ bảng tần số ghép nhóm, nhóm chiều cao \([170;180)\) có tần số là 8.
Tần số tương đối của nhóm này là: \(\frac{8}{{40}}.100\% = 20\% .\)
Vậy tần số tương đối của nhóm này là 20%.
Đáp án: 20
Bạn An giải một đề thi gồm có ba bài được đánh số 1; 2; 3. An được chọn lần lượt các bài để giải theo một thứ tự ngẫu nhiên. Tính xác suất của biến cố A: “An giải bài 1 trước bài 3” (viết dưới dạng số thập phân)
Đáp án:
Đáp án:
Xác định số phần tử của không gian mẫu và số phần tử của biến cố.
Xác suất của biến cố bằng tỉ số giữa số phần tử của biến cố với số phần tử của không gian mẫu.
Không gian mẫu của phép thử là: \(\Omega \) = {(1;2;3),(1;3;2),(2;1;3),(2;3;1),(3;1;2),(3;2;1)}. Không gian mẫu có 6 phần tử.
Kết quả thuận lợi cho biến cố A: “An giải bài 1 trước bài 3” là: {(1;2;3),(1;3;2),(2;1;3)}. Biến cố A có 3 phần tử.
Xác suất của biến cố A: “An giải bài 1 trước bài 3” là: \(\frac{3}{6} = \frac{1}{2} = 0,5\).
Đáp án: 0,5
Cho lục giác đều ABCDEF nội tiếp đường tròn (O). Phép quay thuận chiều \(\alpha ^\circ \) tâm O biến điểm A thành điểm C. Giá trị của \(\alpha \) là
Đáp án:
Đáp án:
Tính số đo mỗi góc ở tâm ứng với một cạnh: \(\frac{{360^\circ }}{n}\) (với n là số cạnh của đa giác)
Xác định góc quay từ A đến C là \(\widehat {AOC}\).
Ta có mỗi góc ở tâm ứng với mỗi cạnh của lục giác đều là:
\(\widehat {AOB} = \widehat {BOC} = \widehat {COD} = \widehat {DOE} = \widehat {EOF} = \widehat {FOA} = \frac{{360^\circ }}{6} = 60^\circ \).
Suy ra \(\widehat {AOC} = 60^\circ .2 = 120^\circ \) nên phép quay thuận chiều \(\alpha ^\circ = 120^\circ \) tâm O biến điểm A thành điểm C. Do đó \(\alpha = 120\).
Đáp án: 120
a) Thay tung độ bằng 8 vào hàm số \(y = \frac{{ - 1}}{4}{x^2}\) để tìm hoành độ của M tương ứng.
b) Dùng \(ac < 0\) để xác định số nghiệm của phương trình.
Tính tổng và tích của hai nghiệm \({x_1},{x_2}\) theo định lí Viète: \(\left\{ \begin{array}{l}S = {x_1} + {x_2} = \frac{{ - b}}{a}\\P = {x_1}{x_2} = \frac{c}{a}\end{array} \right.\).
Biến đổi biểu thức A để xuất hiện tổng và tích của hai nghiệm.
a) Thay y = 8 ta được:
\(\begin{array}{l}8 = \frac{1}{2}{x^2}\\{x^2} = 8:\frac{1}{2}\\{x^2} = 16\\x = \pm 4\end{array}\)
Vậy toạ độ của điểm M là: \(M\left( { - 4;8} \right);M\left( {4;8} \right)\).
b) Xét phương trình \({x^2} - 2x - 8 = 0\) ta có: \(ac = 1.\left( { - 8} \right) = - 8 < 0\) nên phương trình có hai nghiệm phân biệt \({x_1};{x_2}\).
Áp dụng định lí Viète, ta có: \(\left\{ \begin{array}{l}S = {x_1} + {x_2} = - \frac{{\left( { - 2} \right)}}{1} = 2\\P = {x_1}.{x_2} = \frac{{ - 8}}{1} = - 8\end{array} \right.\)
Ta có: \(A = \left( {{x_1} + 2{x_2}} \right)\left( {{x_2} + 2{x_1}} \right)\)
\(\begin{array}{l} = {x_1}{x_2} + 2x_2^2 + 2x_1^2 + 4{x_1}{x_2}\\ = {x_1}{x_2} + 2{\left( {{x_1} + {x_2}} \right)^2}\\ = - 8 + {2.2^2} = 0\end{array}\)
Vậy \(A = 0\).
a) Chứng minh \(\Delta BEC\) và \(\Delta BDC\) cùng nội tiếp đường tròn đường kính BC nên tứ giác BCDE nội tiếp.
b) Chứng minh \(\widehat {ADE} = \widehat {AKC}\) dựa vào tổng hai góc đối của tứ giác nội tiếp BCDE và tính chất hai góc kề bù.
Suy ra $\Delta ADF\backsim \Delta AKC$ nên \(\widehat {AFD} = 90^\circ \) suy ra AK \( \bot \)DE
c) Chứng minh H là trực tâm của \(\Delta ABC\) suy ra AH \( \bot \) BC
Chứng minh tứ giác ABGD nội tiếp đường tròn đường kính AB
suy ra đường kính đường tròn ngoại tiếp \(\Delta ADG\) là AB
Chứng minh $\Delta ABG\backsim \Delta AKC$ suy ra \(\frac{{AB}}{{AK}} = \frac{{AG}}{{AC}}\)
Sử dụng tỉ số lượng giác \(\sin \widehat {ACB} = \frac{{AG}}{{AC}}\) nên \(\frac{{AB}}{{AK}} = \sin \widehat {ACB}\)
Giải để tính AB.
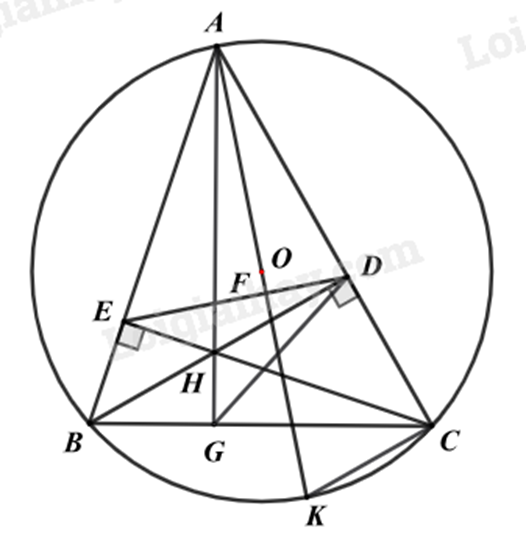
a) Vì BD và CE là hai đường cao của tam giác ABC nên \(\widehat {BEC} = \widehat {BDC} = 90^\circ \)
Xét \(\Delta BEC\) vuông tại E nên \(\Delta BEC\) nội tiếp đường tròn đường kính BC, do đó B, E, C thuộc đường tròn đường kính BC.
Xét \(\Delta BDC\) vuông tại D nên \(\Delta BDC\) nội tiếp đường tròn đường kính BC, do đó B, D, C thuộc đường tròn đường kính BC.
Do đó bốn điểm B, C, D, E thuộc đường tròn đường kính BC hay \(BCDE\) là tứ giác nội tiếp.
b) Vì BCDE là tứ giác nội tiếp nên \(\widehat {CBE} + \widehat {EDC} = 180^\circ \) (tổng hai góc đối của tứ giác nội tiếp)
và \(\widehat {ADE} + \widehat {EDC} = 180^\circ \) (hai góc kề bù) suy ra \(\widehat {CBE} = \widehat {ADE}\)
Mà \(\widehat {CBE} = \widehat {AKC}\) (hai góc nội tiếp cùng chắn cung AC). Do đó \(\widehat {ADE} = \widehat {AKC}\)
Xét \(\Delta ADF\) và \(\Delta AKC\) có:
\(\widehat A\) chung
\(\widehat {ADF} = \widehat {AKC}\) (\(\widehat {ADE} = \widehat {AKC}\))
nên $\Delta ADF\backsim \Delta AKC$ suy ra \(\widehat {AFD} = \widehat {ACK} = 90^\circ \) (hai góc tương ứng và \(\widehat {ACK}\) là góc nội tiếp chắn nửa đường tròn)
Do đó AK \( \bot \)DE
c) Vì BD và CE là hai đường cao của tam giác ABC và BD cắt CE tại H nên H là trực tâm của \(\Delta ABC\) suy ra AH \( \bot \) BC tại G.
Xét \(\Delta ABD\) vuông tại D nên \(\Delta ABD\) nội tiếp đường tròn đường kính AB, do đó A, B, D thuộc đường tròn đường kính AB.
Xét \(\Delta ABG\) vuông tại G nên \(\Delta ABG\) nội tiếp đường tròn đường kính AB, do đó A, B, G thuộc đường tròn đường kính AB.
Do đó bốn điểm A, B, G, D thuộc đường tròn đường kính AB hay tứ giác ABGD nội tiếp đường tròn đường kính AB.
Suy ra đường kính đường tròn ngoại tiếp \(\Delta ADG\) là AB.
Xét \(\Delta ABG\) và \(\Delta AKC\) có:
\(\widehat {AGB} = \widehat {ACK}\left( { = 90^\circ } \right)\)
\(\widehat {ABG} = \widehat {AKC}\) (hai góc nội tiếp cùng chắn cung AC)
nên $\Delta ABG\backsim \Delta AKC$ suy ra \(\frac{{AB}}{{AK}} = \frac{{AG}}{{AC}}\)
Áp dụng tỉ số lượng giác vào tam giác vuông AGC, ta có: \(\sin \widehat {ACB} = \frac{{AG}}{{AC}}\)
Suy ra \(\frac{{AB}}{{AK}} = \sin \widehat {ACB}\).
Thay số, ta được:
\(\frac{{AB}}{{2.5}} = \sin 60^\circ \) suy ra \(AB = \sin 60^\circ .2.5 = 5\sqrt 3 \approx 8,7\left( {cm} \right)\)
Vậy đường kính đường tròn ngoại tiếp \(\Delta ADG\) khoảng 8,7cm.
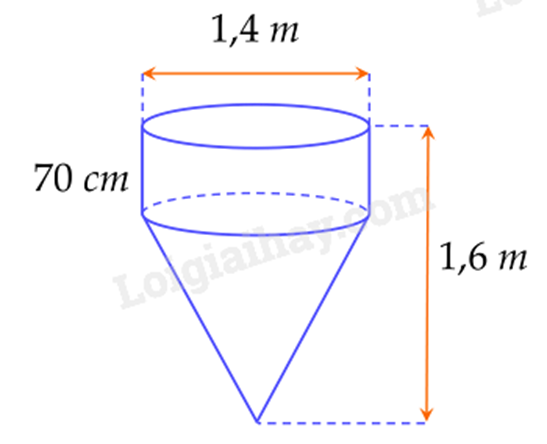
Thể tích của dụng cụ trộn bê tông = thể tích hình trụ + thể tích hình nón.
Sử dụng công thức tính thể tích hình trụ: \({V_T} = \pi {r^2}h\).
Sử dụng công thức tính thể tích hình nón: \({V_N} = \frac{1}{3}\pi {r^2}h\).
Đổi 70cm = 0,7m
Bán kính đáy của dụng cụ là:
\(r = 1,4:2 = 0,7\left( m \right)\)
Thể tích phần dạng hình trụ là:
\({V_T} = \pi {r^2}{h_1} \approx 3,14.0,{7^2}.0,7 \approx 1,08\left( {{m^3}} \right)\)
Chiều cao phần dạng hình nón là:
\({h_2} = 1,6 - 0,7 = 0,9\left( m \right)\)
Thể tích phần dạng hình nón là:
\({V_N} = \frac{1}{3}.\pi {r^2}{h_2} \approx \frac{1}{3}.3,14.0,{7^2}.0,9 \approx 0,46\left( {{m^3}} \right)\)
Thể tích của dụng cụ trộn bê tông là: \({V_T} + {V_N} \approx 1,08 + 0,46 = 1,54\left( {{m^3}} \right)\)
Vậy thể tích của dụng cụ trộn bê tông là khoảng \(1,54{m^3}\).
Phần I. Câu hỏi trắc nghiệm nhiều phương án lựa chọn (3 điểm) Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Phần I. Câu hỏi trắc nghiệm nhiều phương án lựa chọn (3 điểm) Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
