Đề thi giữa kì 2 Toán 7 Chân trời sáng tạo - Đề số 9

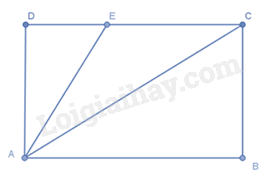
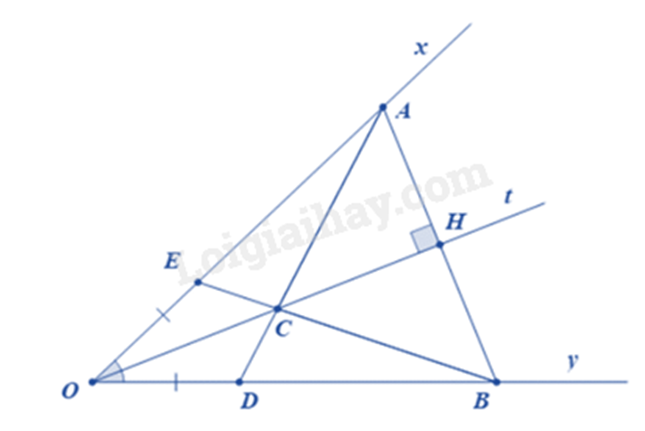
a) Xét tam giác AHO và tam giác BHO có:

\(\widehat {AOH} = \widehat {BOH}\) (Ot là tia phân giác của \(\widehat {AOB}\))

OH chung

\(\widehat {AHO} = \widehat {BHO}\left( { = {{90}^0}} \right)\)

Suy ra \(\Delta AHO = \Delta BHO\left( {g.c.g} \right)\)

Suy ra OA = OB (hai cạnh tương ứng) (đpcm)

b) \(\Delta AHO = \Delta BHO\) suy ra AH = HB (hai cạnh tương ứng)

Xét tam giác AHC và tam giác BHC có:

HC chung

\(\widehat {AHC} = \widehat {BHC}\left( { = {{90}^0}} \right)\)

AH = HB

Suy ra \(\Delta AHC = \Delta BHC\) (hai cạnh góc vuông)

Suy ra \(\widehat {ACH} = \widehat {HCB}\) (hai góc tương ứng)

c) Xét tam giác OCE và OCD có:

OE = OD

\(\widehat {EOC} = \widehat {DOC}\)

OC chung

Suy ra ∆OEC = ∆ODC (c.g.c)

Suy ra EC = DC (hai cạnh tương ứng)

Ta có OA = OB và OE = OD nên AE = BD.

Xét \(\Delta ECA\) và \(\Delta DCB\) có:

EC = ED (cmt)

EA = DB (cmt)

CA = CB (\(\Delta AHC = \Delta BHC\))

Suy ra \(\Delta ECA = \Delta DCB\) (c.c.c)

Suy ra \(\widehat {ECA} = \widehat {DCB}\) (hai góc tương ứng)

Mặt khác \(\widehat {ECA} + \widehat {ECD} = {180^0}\) (vì AC cắt Oy tại D)

Suy ra \(\widehat {DCB} + \widehat {ECD} = {180^0}\) hay B, C, E thẳng hàng (đpcm).