 Đề thi toán 7, đề kiểm tra toán 7 chân trời sáng tạo có đáp án và lời giải chi tiết
Đề thi toán 7, đề kiểm tra toán 7 chân trời sáng tạo có đáp án và lời giải chi tiết
 Đề thi học kì 1 Toán 7 Chân trời sáng tạo
Đề thi học kì 1 Toán 7 Chân trời sáng tạo Đề thi học kì 1 Toán 7 - Đề số 6 - Chân trời sáng tạo
Tải vềPhần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Đề bài
Phần I: Trắc nghiệm (3 điểm).
Câu 1: Trong các phân số sau, phân số nào biểu diễn số hữu tỉ \( - 0,125?\)
A. \(\dfrac{1}{8}\)
B. \( - \dfrac{1}{8}\)
C. \( - \dfrac{1}{{125}}\)
D. \(\dfrac{1}{{125}}\)
Câu 2: Kết quả của phép tính: \({\left( { - 0,08} \right)^4}{.10^4}\) là:
A. \(0,{8^4}\)
B. \({8^4}\)
C. \({10.8^4}\)
D. \(0,{08^4}\)
Câu 3: So sánh \(2 + \sqrt {37} \) và \(6 + \sqrt 2 \)?
A. \(2 + \sqrt {37} > 6 + \sqrt 2 \)
B. \(2 + \sqrt {37} < 6 + \sqrt 2 \)
C. \(2 + \sqrt {37} = 6 + \sqrt 2 \)
D. Không có đáp án
Câu 4: Sắp xếp các số \(\left| { - 3} \right|\,\,;\,\,\sqrt 6 \,\,;\,\,\left| {\dfrac{{ - 22}}{6}} \right|\,\,;\,\,\sqrt {\dfrac{{128}}{2}} \,\,;\,\, - \dfrac{7}{3}\) theo thứ tự tăng dần.
A. \( - \dfrac{7}{3}\,\,;\,\,\left| {\dfrac{{ - 22}}{6}} \right|\,\,;\,\,\sqrt 6 \,\,;\,\,\left| { - 3} \right|\,\,;\,\,\sqrt {\dfrac{{128}}{2}} \)
B. \( - \dfrac{7}{3}\,\,;\,\,\sqrt 6 \,;\,\,\left| { - 3} \right|\,\,\,;\,\,\left| {\dfrac{{ - 22}}{6}} \right|\,\,;\,\,\sqrt {\dfrac{{128}}{2}} \)
C. \(\,\sqrt {\dfrac{{128}}{2}} \,\,;\,\,\,\left| { - 3} \right|\,\,;\left| {\dfrac{{ - 22}}{6}} \right|\,\,;\,\,\,\sqrt 6 \,\,;\,\, - \dfrac{7}{3}\,\,\)
D. \( - \dfrac{7}{3}\,\,\,;\,\,\sqrt 6 \,\,;\,\,\,\left| {\dfrac{{ - 22}}{6}} \right|\,\,;\,\,\sqrt {\dfrac{{128}}{2}} \,\,;\,\,\,\left| { - 3} \right|\)
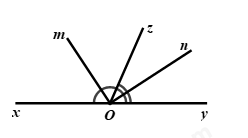
Câu 5: Cho góc bẹt \(xOy\). Vẽ tia \(Oz\) nằm giữa hai tia \(Ox\) và \(Oy\). Vẽ tia \(Om\) là phân giác của góc \(xOz\). Vẽ tia \(On\) là tia phân giác của góc \(zOy\). Tính số đo góc \(mOn?\)
A. \(\angle mOn = {30^0}\)
B. \(\angle mOn = {60^0}\)
C. \(\angle mOn = {90^0}\)
D. \(\angle mOn = {120^0}\)
Câu 6: Trong các khẳng định sau, khẳng định nào sai?
A. Hình lăng trụ đứng tam giác có 4 mặt, 6 đỉnh
B. Hình lăng trụ đứng tam giác có 5 mặt, 6 đỉnh
C. Công thức tính diện tích xung quanh của hình lăng trụ đứng tứ giác và tam giác là \({S_{xq}} = C.h\)
D. Hình lăng trụ đứng tứ giác là lăng trụ đứng tứ giác có các mặt bên là các hình chữ nhật
Câu 7: Một hình khối gồm 14 hình lập phương gắn kết với nhau như hình bên dưới. Mỗi hình lập phương có cạnh \(1\,cm.\) Thể tích của hình khối này là:
A. \(15\,c{m^3}\)
B. \(14\,cm\)
C. \(27\,c{m^3}\)
D. \(14\,c{m^3}\)
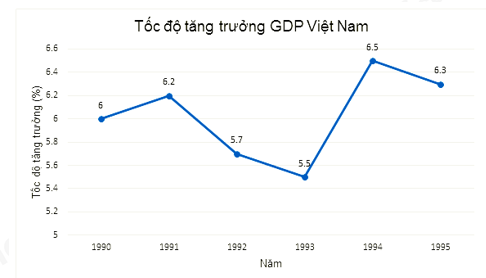
Câu 8: Cho biểu đồ sau:
Tốc độ tăng trưởng GDP Việt Nam mạnh nhất trong khoảng thời gian từ năm 1990 đến năm 1995 là năm nào? Bao nhiêu % ?
A. Năm 1991 tăng 6,2%
B. Năm 1995 tăng 6,5%
C. Năm 1994 tăng 6,7%
D. Năm 1994 tăng 6,5%
Câu 9: Đường trung trực của đoạn thẳng \(AB\) là đường thẳng …
A. song song với đoạn thẳng \(AB\).
B. vuông góc với đoạn thẳng \(AB\).
C. đi qua trung điểm của đoạn thẳng \(AB\).
D. vuông góc với đoạn thẳng \(AB\) tại trung điểm của nó.
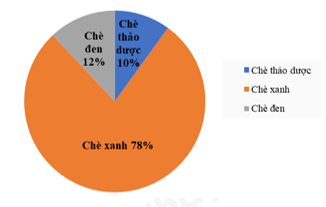
Câu 10: Trong năm 2020, công ty chè Phú Minh thu được 25 tỉ đồng từ việc xuất khẩu chè. Biểu đồ hình quạt tròn ở hình bên dưới biểu diễn kết quả thống kê (tính theo tỉ số phần trăm) các loại chè xuất khẩu trong năm 2020 của công ty Phú Minh.
Bảng nào sau đây là bảng số liệu thống kê số tiền công ty chè Phú Minh thu được ở mỗi loại chè 2020?
A.
|
Loại chè |
Chè thảo dược |
Chè xanh |
Chè đen |
|
Số tiền (tỉ đồng) |
2,5 |
19,1 |
3,2 |
B.
|
Loại chè |
Chè thảo dược |
Chè xanh |
Chè đen |
|
Số tiền (tỉ đồng) |
2,5 |
19,5 |
3 |
C.
|
Loại chè |
Chè thảo dược |
Chè xanh |
Chè đen |
|
Số tiền (tỉ đồng) |
2,2 |
19,2 |
3 |
D.
|
Loại chè |
Chè thảo dược |
Chè xanh |
Chè đen |
|
Số tiền (tỉ đồng) |
2,4 |
19 |
3,6 |
Phần II. Tự luận (7 điểm):
Bài 1: (2,0 điểm )
Thực hiện phép tính:
a) \(\left( { - \dfrac{3}{4} + \dfrac{2}{3}} \right):\dfrac{5}{{11}} + \left( { - \dfrac{1}{4} + \dfrac{1}{3}} \right):\dfrac{5}{{11}}\)
b) \(\dfrac{{{{27}^{10}}{{.16}^{25}}}}{{{6^{30}}{{.32}^{15}}}}\)
c) \(\left| {\dfrac{3}{5} - \dfrac{1}{{10}}} \right| - \sqrt {\dfrac{{36}}{{25}}} + {\left( {\dfrac{3}{{10}}} \right)^5}:{\left( {\dfrac{3}{{10}}} \right)^4}\)
d) \(\sqrt {144} + \sqrt {49} - 10\sqrt {\dfrac{4}{{25}}} \)
Bài 2: (2,0 điểm)
Tìm \(x\), biết:
a) \(\left( { - \dfrac{1}{2}} \right) + \left( {\dfrac{4}{5} + x} \right) = 1\dfrac{1}{2}\)
b) \({\left( {x - \dfrac{1}{3}} \right)^2} = \dfrac{1}{9}\)
c) \(5.\sqrt x - \sqrt {\dfrac{1}{{25}}} = 0\)
d) \(\left| {0,3 - x} \right| = \dfrac{1}{3}\)
Bài 3: (1,0 điểm)
Tìm số đo của góc \(QRS\) trong hình vẽ bên dưới, biết \(aa'//bb'.\)
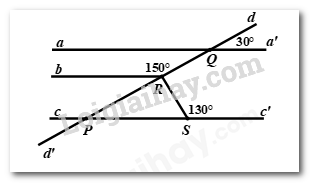
Bài 4: (1,5 điểm)
Phần bên trong của một cái khuôn làm bánh (không có nắp) có dạng hình hộp chữ nhật với đáy là hình vuông cạnh là \(20\,cm,\) chiều cao \(5\,cm.\) Người ta dự định sơn phần bên trong bằng loại sơn không dính. Hỏi với một lượng sơn đủ bao phủ được \(100\,{m^2}\) thì sơn được bao nhiêu cái khuôn làm bánh?
Bài 5: (0,5 điểm)
Tìm số thực \(x\), biết: \(\left| x \right| + \left| {x + 2} \right| = 0\).
Lời giải
Phần I: Trắc nghiệm
|
1.B |
2.A |
3.A |
4.B |
5.C |
6.A |
7.D |
8.D |
9.D |
10.B |
Câu 1
Phương pháp:
Đưa số thập phân về phân số.
Cách giải:
Ta có: \( - 0,125 = - \dfrac{{125}}{{1000}} = - \dfrac{1}{8}\)
Vậy phân số biểu diễn số hữu tỉ \( - 0,125\) là \( - \dfrac{1}{8}\).
Chọn B.
Câu 2
Phương pháp:
Vận dụng công thức tính lũy thừa của một tích bằng tích các lũy thừa: \({\left( {x.y} \right)^n} = {x^n}.{y^n}\)
\({\left( { - a} \right)^{2.k}} = {a^{2.k}}\left( {k \in N} \right)\)
Cách giải:
\({\left( { - 0,08} \right)^4}{.10^4} = {\left( { - 0,08.10} \right)^4} = {\left( { - 0,8} \right)^4} = 0,{8^4}\)
Chọn A.
Câu 3
Phương pháp:
So sánh từng số hạng của tổng.
Cách giải:
Ta có: \(2 = \sqrt {{2^2}} = \sqrt 4 \,\,;\,\,6 = \sqrt {{6^2}} = \sqrt {36} \)
Vì \(4 > 2\) nên \(\sqrt 4 > \sqrt 2 \) hay \(2 > \sqrt 2 \)
\(37 > 36\) nên \(\sqrt {37} > \sqrt {36} \) hay \(\sqrt {37} > 6\)
Do đó, \(2 + \sqrt {37} > 6 + \sqrt 2 \)
Chọn A.
Câu 4
Phương pháp:
Tính giá trị tuyệt đối của một số thực, tính căn bậc hai của một số thực.
Thực hiện so sánh các số để sắp xếp thứ tự các số.
Cách giải:
Ta có:
\(\begin{array}{l}\left| { - 3} \right| = - \left( { - 3} \right) = 3\\\left| {\dfrac{{ - 22}}{6}} \right| = - \left( {\dfrac{{ - 22}}{6}} \right) = \dfrac{{22}}{6} = \dfrac{{11}}{3}\\\sqrt {\dfrac{{128}}{2}} = \sqrt {64} = \sqrt {{8^2}} = 8\end{array}\)
Ta có: \(3 = \dfrac{9}{3}\,\,;\,\,8 = \dfrac{{24}}{3}\)
Vì \(9 < 11 < 24\) nên \(\dfrac{9}{3} < \dfrac{{11}}{3} < \dfrac{{24}}{3}\) hay \(3 < \dfrac{{11}}{3} < 8\)
Mặt khác, ta có: \(3 = \sqrt {{3^2}} = \sqrt 9 \)
Vì \(6 < 9\) nên \(\sqrt 6 < \sqrt 9 \) hay \(\sqrt 6 < 3\)
Do đó, \(\sqrt 6 < 3 < \dfrac{{11}}{3} < 8\)
Mà \( - \dfrac{7}{3} < 0\) nên ta có: \( - \dfrac{7}{3} < \sqrt 6 < 3 < \dfrac{{11}}{3} < 8\) hay \( - \dfrac{7}{3} < \sqrt 6 < \left| { - 3} \right| < \left| {\dfrac{{ - 22}}{6}} \right| < \sqrt {\dfrac{{128}}{2}} \)
Vậy thứ tự tăng dần của các số là: \( - \dfrac{7}{3}\,\,;\,\,\sqrt 6 \,;\,\,\left| { - 3} \right|\,\,\,;\,\,\left| {\dfrac{{ - 22}}{6}} \right|\,\,;\,\,\sqrt {\dfrac{{128}}{2}} \).
Chọn B.
Câu 5
Phương pháp:
\(Oz\) là tia phân giác của góc \(xOy\) thì ta có: \(\angle xOz = \angle zOy = \dfrac{{\angle xOy}}{2}\)
Cách giải:
Vì \(Om\) là tia phân giác của góc \(xOz\) nên \(\angle zOm = \dfrac{{\angle xOz}}{2}\) hay \(\angle xOz = 2.\angle zOm\)
Vì \(On\) là tia phân giác của góc \(zOy\) nên \(\angle nOz = \dfrac{{\angle zOy}}{2}\) hay \(\angle zOy = 2.\angle nOz\)
Vì \(\angle xOz\) và \(\angle zOy\) là hai góc kề bù nên \(\angle xOy + \angle zOy = {180^0}\)
\(\begin{array}{l} \Rightarrow 2.\angle zOm + 2.\angle nOz = {180^0}\\ \Rightarrow 2.\left( {\angle zOm + \angle nOz} \right) = {180^0}\\ \Rightarrow \angle zOm + \angle nOz = {180^0}:2\\ \Rightarrow \angle zOm + \angle nOz = {90^0}\end{array}\)
Vì \(Oz\) nằm giữa hai tia \(Om\) và \(On\) nên \(\angle zOm + \angle nOz = \angle mOn = {90^0}\)
Vậy \(\angle mOn = {90^0}\)
Chọn C.
Câu 6
Phương pháp:
|
|
Hình lăng trụ đứng tam giác |
Hình lăng trụ đứng tứ giác |
|
Số mặt |
5 |
6 |
|
Số đỉnh |
6 |
8 |
|
Số cạnh |
9 |
12 |
|
Số mặt đáy |
2 |
2 |
|
Số mặt bên |
3 |
4 |
Các mặt bên của hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác đều là các hình chữ nhật.
Diện tích xung quanh của hình năng trụ đứng tam giác (lăng trụ đứng tứ giác)là: \({S_{xq}} = C.h\) (trong đó \(C\) là chu vi đáy và \(h\) là chiều cao của hình lăng trụ)
Cách giải:
Hình lăng trụ đứng tam giác có 4 mặt, 6 đỉnh \( \Rightarrow \,\)Sai
Hình lăng trụ đứng tam giác có 5 mặt, 6 đỉnh \( \Rightarrow \,\)Đúng
Công thức tính diện tích xung quanh của hình lăng trụ đứng tứ giác và tam giác là \({S_{xq}} = C.h\) \( \Rightarrow \,\)Đúng
Hình lăng trụ đứng tứ giác là lăng trụ đứng tứ giác có các mặt bên là các hình chữ nhật \( \Rightarrow \,\)Đúng
Chọn A.
Câu 7
Phương pháp:
Áp dụng công thức tính thể tích của hình lập phương là \(V = {a^3}\) (trong đó \(a\) là 1 cạnh của hình lập phương)
Bước 1: Tính thể tích của 1 khối lập phương nhỏ có cạnh \(1cm.\)
Bước 2: Tính thể tích của khối hình đã cho (lấy tổng số khối lập phương cạnh \(1cm\)nhân với thể tích của một khối lập phương cạnh \(1cm\)).
Cách giải:
Thể tích của khối lập phương nhỏ cạnh \(1cm\) là: \({V_1} = {1^3} = 1\left( {c{m^3}} \right)\)
Thể tích của khối hình đã cho là: \(V = 14.{V_1} = 14.1 = 14\left( {c{m^3}} \right)\)
Chọn D.
Câu 8
Phương pháp:
Quan sát biểu đồ.
Cách giải:
Theo biểu đồ ta thấy:
Tốc độ tăng trưởng GDP Việt Năm năm 1991 là 6,2%
Tốc độ tăng trưởng GDP Việt Năm năm 1994 là 6,5%
Tốc độ tăng trưởng GDP Việt Năm năm 1995 là 6,3%
Tốc độ tăng trưởng GDP Việt Năm năm 1994 là 6,5% là điểm cao nhất trên biểu đồ nên tại năm 1994 có tốc độ tăng trưởng GPD Việt Nam lớn nhất.
Chọn D.
Câu 9
Phương pháp:
Vận dụng định nghĩa: Đường thẳng vuông góc với một đoạn thẳng tại trung điểm của nó được gọi là đường trung điểm của đoạn thẳng đó.
Cách giải:
Đường trung trực của đoạn thẳng \(AB\) là đường thẳng vuông góc với đoạn thẳng \(AB\) tại trung điểm của nó.
Chọn D.
Câu 10
Phương pháp:
Đọc và mô tả dữ liệu của biểu đồ hình quạt tròn.
Số tiền thu được tương ứng = % tương ứng . toàn bộ số tiền thu được
Cách giải:
Số tiền công ty Phú Minh thu được từ chè thảo dược là: \(10\% .25 = 2,5\) (tỉ đồng)
Số tiền công ty Phú Minh thu được từ chè xanh là: \(78\% .25 = 19,5\) (tỉ đồng)
Số tiền công ty Phú Minh thu được từ chè đen là: \(12\% .25 = 3\) (tỉ đồng)
Ta có bảng số liệu thống kê số tiền công ty chè Phú Minh thu được ở mỗi loại chè 2020:
|
Loại chè |
Chè thảo dược |
Chè xanh |
Chè đen |
|
Số tiền (tỉ đồng) |
2,5 |
19,5 |
3 |
Chọn B.
Phần II. Tự luận:
Bài 1
Phương pháp:
a) Thực hiện các phép toán với các số hữu tỉ
b) Vận dụng quy tắc tính lũy thừa của một lũy thừa: Khi tính lũy thừa của một lũy thừa, ta giữ nguyên cơ số và nhân hai số mũ: \({\left( {{x^m}} \right)^n} = {x^{m.n}}\).
Vận dụng quy tắc tính thương của hai lũy thừa cùng cơ số: Khi chia hai lũy thừa cùng cơ số (khác 0), ta giữ nguyên cơ số và lấy số mũ của lũy thừa bị chia trừ đi số mũ của lũy thừa chia: \({x^m}:{x^n} = {x^{m - n}}\,\left( {x \ne 0;m \ge n} \right)\).
c) Vận dụng kiến thức giá trị tuyệt đối của một số thực: \(\left| x \right| = \left\{ \begin{array}{l}x\,\,\,\,\,\,khi\,\,\,x > 0\\ - x\,\,\,khi\,\,x < 0\\0\,\,\,\,\,\,\,khi\,\,\,x = 0\end{array} \right.\)
Tính toán với căn bậc hai của một số thực
Vận dụng quy tắc tính thương của hai lũy thừa cùng cơ số: Khi chia hai lũy thừa cùng cơ số (khác 0), ta giữ nguyên cơ số và lấy số mũ của lũy thừa bị chia trừ đi số mũ của lũy thừa chia: \({x^m}:{x^n} = {x^{m - n}}\,\left( {x \ne 0;m \ge n} \right)\).
d) Tính toán với căn bậc hai của một số thực
Cách giải:
a) \(\left( { - \dfrac{3}{4} + \dfrac{2}{3}} \right):\dfrac{5}{{11}} + \left( { - \dfrac{1}{4} + \dfrac{1}{3}} \right):\dfrac{5}{{11}}\)
\(\begin{array}{l} = \left( { - \dfrac{3}{4} + \dfrac{2}{3}} \right).\dfrac{{11}}{5} + \left( { - \dfrac{1}{4} + \dfrac{1}{3}} \right).\dfrac{{11}}{5}\\ = \left( { - \dfrac{3}{4} + \dfrac{2}{3} + \dfrac{{ - 1}}{4} + \dfrac{1}{3}} \right).\dfrac{{11}}{5}\\ = \left[ {\left( { - \dfrac{3}{4} + \dfrac{{ - 1}}{4}} \right) + \left( {\dfrac{2}{3} + \dfrac{1}{3}} \right)} \right].\dfrac{{11}}{5}\\ = \left( {\dfrac{{ - 4}}{4} + \dfrac{3}{3}} \right).\dfrac{{11}}{5}\\ = \left( { - 1 + 1} \right).\dfrac{{11}}{5}\\ = 0.\dfrac{{11}}{5} = 0\end{array}\)
b) \(\dfrac{{{{27}^{10}}{{.16}^{25}}}}{{{6^{30}}{{.32}^{15}}}}\)
\(\begin{array}{l} = \dfrac{{{{\left( {{3^3}} \right)}^{10}}.{{\left( {{2^4}} \right)}^{25}}}}{{{{\left( {2.3} \right)}^{30}}.{{\left( {{2^5}} \right)}^{15}}}} = \dfrac{{{3^{3.10}}{{.2}^{4.25}}}}{{{2^{30}}{{.3}^{30}}{{.2}^{5.15}}}}\\ = \dfrac{{{3^{30}}{{.2}^{100}}}}{{{2^{30}}{{.3}^{30}}{{.2}^{75}}}} = \dfrac{{{2^{100}}}}{{{2^{30 + 75}}}}\\ = \dfrac{{{2^{100}}}}{{{2^{105}}}} = \dfrac{1}{{{2^5}}} = \dfrac{1}{{32}}\end{array}\)
c) \(\left| {\dfrac{3}{5} - \dfrac{1}{{10}}} \right| - \sqrt {\dfrac{{36}}{{25}}} + {\left( {\dfrac{3}{{10}}} \right)^5}:{\left( {\dfrac{3}{{10}}} \right)^4}\)
\(\begin{array}{l} = \left| {\dfrac{6}{{10}} - \dfrac{1}{{10}}} \right| - \dfrac{6}{5} + {\left( {\dfrac{3}{{10}}} \right)^{5 - 4}}\\ = \left| {\dfrac{5}{{10}}} \right| - \dfrac{6}{5} + {\left( {\dfrac{3}{{10}}} \right)^1}\\ = \dfrac{5}{{10}} - \dfrac{{12}}{{10}} + \dfrac{3}{{10}}\\ = \dfrac{{ - 4}}{{10}} = \dfrac{{ - 2}}{5}\end{array}\)
d) \(\sqrt {144} + \sqrt {49} - 10\sqrt {\dfrac{4}{{25}}} \)
\(\begin{array}{l} = 12 + 7 - 10.\dfrac{2}{5}\\ = 19 - 4\\ = 15\end{array}\)
Bài 2
Phương pháp:
a) Thực hiện các phép toán với số hữu tỉ, vận dụng quy tắc chuyển vế tìm \(x\)
b) Giải \({\left[ {A\left( x \right)} \right]^2} = {a^2} = {\left( { - a} \right)^2}\)
Trường hợp 1: \(A\left( x \right) = a\)
Trường hợp 2: \(A\left( x \right) = - a\)
c) Vận dụng kiến thức căn bậc hai số học của số thực, tìm \(x\)
d) \(\left| x \right| = a\)
Trường hợp \(a < 0\), khi đó phương trình không có nghiệm \(x\)
Trường hợp \(a > 0\), vận dụng kiến thức giá trị tuyệt đối của một số thực: \(\left| x \right| = \left\{ \begin{array}{l}x\,\,\,\,\,\,khi\,\,\,x > 0\\ - x\,\,\,khi\,\,x < 0\\0\,\,\,\,\,\,\,khi\,\,\,x = 0\end{array} \right.\)
Cách giải:
a) \(\left( { - \dfrac{1}{2}} \right) + \left( {\dfrac{4}{5} + x} \right) = 1\dfrac{1}{2}\)
\(\begin{array}{l} - \dfrac{1}{2} + \dfrac{4}{5} + x = \dfrac{3}{2}\\x = \dfrac{3}{2} - \left( { - \dfrac{1}{2}} \right) - \dfrac{4}{5}\\x = \dfrac{3}{2} + \dfrac{1}{2} - \dfrac{4}{5}\\x = \dfrac{4}{2} - \dfrac{4}{5}\\x = 2 - \dfrac{4}{5}\\x = \dfrac{{10}}{5} - \dfrac{4}{5}\\x = \dfrac{6}{5}\end{array}\)
Vậy \(x = \dfrac{6}{5}\)
b) \({\left( {x - \dfrac{1}{3}} \right)^2} = \dfrac{1}{9}\)
\({\left( {x - \dfrac{1}{3}} \right)^2} = {\left( {\dfrac{1}{3}} \right)^2} = {\left( { - \dfrac{1}{3}} \right)^2}\)
Trường hợp 1:
\(\begin{array}{l}x - \dfrac{1}{3} = \dfrac{1}{3}\\x = \dfrac{1}{3} + \dfrac{1}{3}\\x = \dfrac{2}{3}\end{array}\)
Trường hợp 2:
\(\begin{array}{l}x - \dfrac{1}{3} = - \dfrac{1}{3}\\x = \dfrac{{ - 1}}{3} + \dfrac{1}{3}\\x = 0\end{array}\)
Vậy \(x \in \left\{ {\dfrac{2}{3};0} \right\}\)
c) \(5.\sqrt x - \sqrt {\dfrac{1}{{25}}} = 0\)
\(\begin{array}{l}5.\sqrt x - \dfrac{1}{5} = 0\\5.\sqrt x = \dfrac{1}{5}\\\sqrt x = \dfrac{1}{5}:5 = \dfrac{1}{5}.\dfrac{1}{5} = \dfrac{1}{{25}}\end{array}\)
\(\begin{array}{l}\sqrt x = \sqrt {{{\left( {\dfrac{1}{{25}}} \right)}^2}} \\ \Rightarrow x = \dfrac{1}{{625}}\end{array}\)
Vậy \(x = \dfrac{1}{{625}}\)
d) \(\left| {0,3 - x} \right| = \dfrac{1}{3}\)
\(\left| {\dfrac{3}{{10}} - x} \right| = \dfrac{1}{3}\)
Trường hợp 1:
\(\begin{array}{l}\dfrac{3}{{10}} - x = \dfrac{1}{3}\\x = \dfrac{3}{{10}} - \dfrac{1}{3}\\x = \dfrac{9}{{30}} - \dfrac{{10}}{{30}}\\x = \dfrac{{ - 1}}{{30}}\end{array}\)
Vậy \(x \in \left\{ {\dfrac{{ - 1}}{{30}};\dfrac{{19}}{{30}}} \right\}\)
Trường hợp 2:
\(\begin{array}{l}\dfrac{3}{{10}} - x = \dfrac{{ - 1}}{3}\\x = \dfrac{3}{{10}} - \left( {\dfrac{{ - 1}}{3}} \right)\\x = \dfrac{9}{{30}} + \dfrac{{10}}{{30}}\\x = \dfrac{{19}}{{30}}\end{array}\)
Bài 3
Phương pháp:
Vận dụng dấu hiệu và tính chất của hai đường thẳng song song.
Vận dụng kiến thức của hai góc kề nhau.
Cách giải:
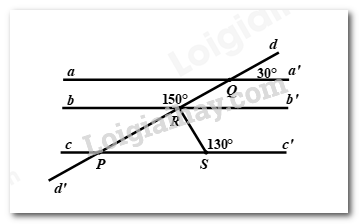
Kẻ \(Rb'\) là tia đối của tia \(Rb\)
Ta có: \(\angle QRb + \angle QRb' = {180^0}\) (hai góc kề bù) nên \(\angle QRb' = {180^0} - \angle QRb = {180^0} - {150^0} = {30^0}\)
Suy ra \(\angle dQa' = \angle QRb'\) (cùng bằng \({30^0}\)). Mà \(\angle dQa',\angle QRb'\) ở vị trí đồng bị nên \(aa'//bb'\).
Do \(aa'//bb'\) nên \(\angle dPc' = \angle dQa' = {30^0}\) (hai góc đồng vị). Vì vậy \(\angle dPc' = \angle QRb'\) (cùng bằng \({30^0}\)).
Mà \(\angle dPc',\angle QRb'\) ở vị trí đồng vị nên \(cc'//bb'\).
Suy ra \(\angle SRb' + \angle RSc' = {180^0}\) (hai góc trong cùng phía) hay \(\angle SRb' = {180^0} - \angle RSc' = {180^0} - {130^0} = {50^0}\)
Do hai góc \(QRb'\) và \(SRb'\) là hai góc kề nhau nên \(\angle QRS = \angle QRb' + \angle SRb' = {30^0} + {50^0} = {80^0}\)
Bài 4
Phương pháp:
Sử dụng công thức tính diện tích xung quanh của hình hộp chữ nhật.
Chú ý: Phải đưa về cùng đơn vị đo
Bước 1: Đổi \(100{m^2} = 1000000c{m^2}\)
Bước 2: Tính diện tích xung quanh của khuôn
Bước 3: Tính diện tích cần sơn của một khuôn
Bước 4: Tính số khuôn sơn được
Cách giải:
Đổi \(100{m^2} = 1000000c{m^2}\)
Diện tích xung quanh của chiếc khuôn là: \({S_{xq}} = 2.\left( {20 + 20} \right).5 = 400\left( {c{m^2}} \right)\)
Diện tích cần được sơn của một chiếc khuôn là: \(S' = {S_{xq}} + S = 400 + \left( {20.20} \right) = 800\left( {c{m^2}} \right)\)
Số chiếc khuôn được sơn là: \(1000000:800 = 1250\)(chiếc)
Bài 5
Phương pháp:
Vận dụng kiến thức về dấu giá trị tuyệt đối: \(\left| {A\left( x \right)} \right| \ge 0\) với mọi số thực \(x\).
Cách giải:
Do \(\left| x \right| \ge 0;\left| {x + 2} \right| \ge 0\) với mọi số thực \(x\) nên \(\left| x \right| + \left| {x + 2} \right| \ge 0\) với mọi số thực \(x\).
Do đó, \(\left| x \right| + \left| {x + 2} \right| = 0\) khi \(\left| x \right| = 0\) và \(\left| {x + 2} \right| = 0\).
Suy ra \(x\) đồng thời bằng \(0\) và bằng \( - 2\) (vô lí).
Vậy không có giá trị nào của \(x\) thỏa mãn yêu cầu của đề bài.
- Đề thi học kì 1 Toán 7 - Đề số 7 - Chân trời sáng tạo
- Đề thi học kì 1 Toán 7 - Đề số 8 - Chân trời sáng tạo
- Đề thi học kì 1 Toán 7 - Đề số 9 - Chân trời sáng tạo
- Đề thi học kì 1 Toán 7 - Đề số 10 - Chân trời sáng tạo
- Đề thi học kì 1 Toán 7 Chân trời sáng tạo - Đề số 11
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 7 - Chân trời sáng tạo - Xem ngay












Danh sách bình luận