Câu hỏi 2 trang 45 SGK Đại số 10
Vẽ parabol...
Đề bài
Vẽ parabol \(y = - 2{x^2} + x + 3\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Xác định đỉnh parabol, trục đối xứng và các giao điểm với hai trục tọa độ.
Lời giải chi tiết
Ta có: \(a = - 2,b = 1,c = 3\)
\(\Delta = {b^2} - 4ac = {1^2} - 4.\left( { - 2} \right).3 = 25\)
\(\begin{array}{l}
- \frac{b}{{2a}} = - \frac{1}{{2.\left( { - 2} \right)}} = \frac{1}{4}\\
- \frac{\Delta }{{4a}} = \frac{{25}}{4}
\end{array}\)
+) Đỉnh \(I\left( {\dfrac{1}{4};\dfrac{{25}}{8}} \right)\)
+) Trục đối xứng là đường thẳng \(x =\dfrac{1}{4}\)
+) Cho \(x=0\) thì \(y=3\).
Giao điểm với trục \(Oy\) là điểm \((0;3)\)
+) Cho \(y=0\) ta có:
\(- 2{x^2} + x + 3 = 0 \Leftrightarrow \left[ \begin{array}{l}
x = - 1\\
x = \frac{3}{2}
\end{array} \right.\)
Giao điểm với trục \(Ox\) là các điểm (\(\dfrac{3}{2}\);0) và \((-1;0)\)
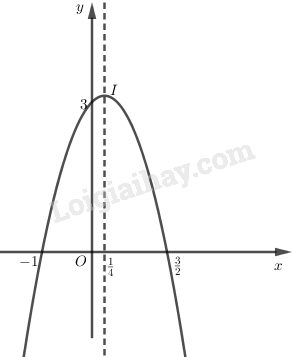
+) Vẽ đồ thị:
Đồ thị hàm số là Parabol có bề lõm hướng xuống dưới \((a = -2 < 0).\)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 1 trang 49 SGK Đại số 10
- Bài 2 trang 49 SGK Đại số 10
- Bài 3 trang 49 SGK Đại số 10
- Bài 4 trang 50 SGK Đại số 10
- Câu hỏi 1 trang 42 SGK Đại số 10
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
