Tích phân \(\int\limits_0^3 {x(x - 1) dx} \) có giá trị bằng với giá trị của tích phân nào trong các tích phân dưới đây ?
-
A.
$\int\limits_0^2 {\left( {{x^2} + x - 3} \right)dx} $.
-
B.
$3\int\limits_0^{3\pi } {\sin xdx} $.
-
C.
$\int\limits_0^{\ln \sqrt {10} } {{e^{2x}}dx} $.
-
D.
$\int\limits_0^\pi {\cos (3x + \pi )dx} $.
Tính rõ từng phép tính tích phân để tìm ra kết quả đúng (chỉ tính đến khi nhận được kết quả đúng thì dừng lại)
Ta có : \(\int\limits_0^3 {x(x - 1)dx} \)\( = \int\limits_0^3 {\left( {{x^2} - x} \right)dx} = \left. {\dfrac{{{x^3}}}{3} - \dfrac{{{x^2}}}{2}} \right|_0^3\) \( = 9 - \dfrac{9}{2} = \dfrac{9}{2}\)
+) $\int\limits_0^{\ln \sqrt {10} } {{e^{2x}}dx} = \left. {\dfrac{{{e^{2x}}}}{2}} \right|_0^{\ln \sqrt {10} } = \dfrac{{{e^{2\ln \sqrt {10} }} - 1}}{2} = \dfrac{9}{2}$,
+) $3\int\limits_0^{3\pi } {\sin xdx} = \left. { - 3\cos x} \right|_0^{3\pi } = 6$,
+) $\int\limits_0^2 {\left( {{x^2} + x - 3} \right)dx} = \left. {\left( {\dfrac{{{x^3}}}{3} + \dfrac{{{x^2}}}{2} - 3x} \right)} \right|_0^2 = \dfrac{8}{3} + 2 - 6 = - \dfrac{4}{3}$,
+) $\int\limits_0^\pi {\cos (3x + \pi )dx} = \dfrac{1}{3}\left. {\sin (3x + \pi )} \right|_0^\pi = \dfrac{1}{3}\left( {\sin 4\pi - \sin \pi } \right) = 0$.
Vậy chọn $\int\limits_0^{\ln \sqrt {10} } {{e^{2x}}dx} $
Đáp án : C
Nhập các phép tính sau vào máy tính để thu kết quả:
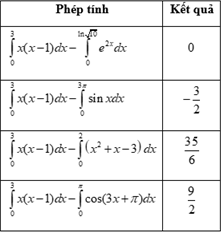
Vậy chọn\(\int\limits_0^{\ln \sqrt {10} } {{e^{2x}}dx} \).








Danh sách bình luận