Tích phân \(I = \int\limits_{\frac{\pi }{3}}^{\frac{\pi }{2}} {\dfrac{{dx}}{{\sin x}}} \) có giá trị bằng
-
A.
\(\dfrac{1}{2}\ln \dfrac{1}{3}\).
-
B.
\(2\ln 3\).
-
C.
\(\dfrac{1}{2}\ln 3\).
-
D.
\(2\ln \dfrac{1}{3}\).
Viết lại tử số \(1 = {\sin ^2}\dfrac{x}{2} + {\cos ^2}\dfrac{x}{2}\) và mẫu số \(\sin x = 2\sin \dfrac{x}{2}\cos \dfrac{x}{2}\) rồi tính tích phân, sử dụng công thức nguyên hàm hàm lượng giác.
Cách 1:
\(\begin{array}{l}I = \int\limits_{\frac{\pi }{3}}^{\frac{\pi }{2}} {\dfrac{{dx}}{{\sin x}}} \\= \int\limits_{\frac{\pi }{3}}^{\frac{\pi }{2}} {\dfrac{{\left( {{{\cos }^2}\dfrac{x}{2} + {{\sin }^2}\dfrac{x}{2}} \right)}}{{2\sin \dfrac{x}{2}\cos \dfrac{x}{2}}}dx} \\ = \dfrac{1}{2}\int\limits_{\frac{\pi }{3}}^{\frac{\pi }{2}} {\left( {\cot \dfrac{x}{2} + \tan \dfrac{x}{2}} \right)dx} \\ = \left. {\left[ {\ln \left| {\sin \dfrac{x}{2}} \right| - \ln \left| {\cos \dfrac{x}{2}} \right|} \right]} \right|_{\frac{\pi }{3}}^{\frac{\pi }{2}}\\ = \left[ {\ln \dfrac{{\sqrt 2 }}{2} - \ln \dfrac{{\sqrt 2 }}{2}} \right] - \left[ {\ln \dfrac{1}{2} - \ln \dfrac{{\sqrt 3 }}{2}} \right]\\ = \ln \sqrt 3 .\end{array}\)
Cách 2:
Bước 1: Dùng máy tính như hình dưới, thu được giá trị \(0,549306...\)
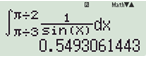
Bước 2: Lấy \({e^{0,549306...}}\) cho kết quả \(1,732050808... \approx \sqrt 3 \). Chọn \(\dfrac{1}{2}\ln 3\).
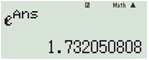
Cách 3:
Thực hiện các phép tính sau trên máy tính (đến khi thu được kết quả bằng \(0\) thì ngưng)
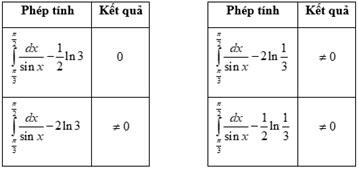
Chọn \(\dfrac{1}{2}\ln 3\).
Đáp án : C
Các bài tập cùng chuyên đề
Cho số thực \(a\) thỏa mãn \(\int\limits_{ - 1}^a {{e^{x + 1}}dx} = {e^2} - 1\), khi đó \(a\) có giá trị bằng
Trong các hàm số dưới đây, hàm số nào có tích phân trên đoạn \([0;\pi ]\) đạt giá trị bằng \(0\) ?
Trong các tích phân sau, tích phân nào có giá trị khác \(2\)?
Tích phân \(I = \int\limits_2^5 {\dfrac{{dx}}{x}} \) có giá trị bằng
Nếu \(\int\limits_{ - 2}^0 {\left( {4 - {e^{ -{\frac{x}{2}}}}} \right)dx} = K - 2e\) thì giá trị của \(K\) là
Tích phân \(I = \int\limits_0^1 {\dfrac{1}{{{x^2} - x - 2}}dx} \) có giá trị bằng
Tích phân \(\int\limits_0^3 {x(x - 1) dx} \) có giá trị bằng với giá trị của tích phân nào trong các tích phân dưới đây ?
Tích phân \(I = \int\limits_1^2 {{x^5}} dx\) có giá trị là:
Tích phân $I = \int\limits_0^1 {\dfrac{{xdx}}{{{{(x + 1)}^3}}}} $ bằng
Cho hai tích phân $I = \int\limits_0^2 {{x^3}dx} $, $J = \int\limits_0^2 {xdx} $. Tìm mối quan hệ giữa $I$ và $J$
Tích phân $I = \int_0^{\dfrac{\pi }{2}} {\dfrac{{4{{\sin }^3}x}}{{1 + \cos x}}} dx$ có giá trị bằng
Tích phân $I = \int\limits_0^{2\pi } {\sqrt {1 + \sin x} } dx$ có giá trị bằng
Tích phân $\int\limits_{ - 1}^5 {\left| {{x^2} - 2x - 3} \right|} dx$ có giá trị bằng:
Tích phân $\int\limits_2^3 {\dfrac{{{x^2} - x + 4}}{{x + 1}}} dx$ bằng
Giá trị của tích phân $I = \int\limits_0^{\frac{\pi }{2}} {\left( {{{\sin }^4}x + {{\cos }^4}x} \right)\left( {{{\sin }^6}x + {{\cos }^6}x} \right)dx} $ là:
Tìm hai số thực \(A,B\) sao cho $f(x) = A\sin \pi x + B$, biết rằng \(f'(1) = 2\) và \(\int\limits_0^2 {f(x)dx = 4} \).
Giá trị của a để đẳng thức \(\int\limits_1^2 {\left[ {{a^2} + (4 - 4a)x + 4{x^3}} \right]dx} = \int\limits_2^4 {2xdx} \) là đẳng thức đúng
Giá trị của tích phân$I = \int\limits_0^2 {\min \left\{ {1,{x^2}} \right\}dx} $ là
Giá trị của tích phân $\int\limits_0^{2017\pi } {\sqrt {1 - \cos 2x} dx} $ là
Biết rằng \(\int\limits_0^{\dfrac{\pi }{4}} {\dfrac{{\cos 2x}}{{{{\left( {\sin x - \cos x + 3} \right)}^2}}}dx = a + \ln b} \) với \(a,b\) là các số hữu tỉ. Giá trị của \(2a + 3b\) bằng
