Bài 4.17 trang 114 SGK Toán 11 tập 1 - Cùng khám phá
Cho hình chóp S.ABCD có đáy là hình thang ABCD với đáy lớn là AD, AD = 2BC. Gọi I, K, L lần lượt là trung điểm của đoạn AD, SA, SD. Chứng minh rằng (SAB) // (ILC) và (SCD) // (BIK).
Đề bài
Cho hình chóp S.ABCD có đáy là hình thang ABCD với đáy lớn là AD, AD = 2BC. Gọi I, K, L lần lượt là trung điểm của đoạn AD, SA, SD. Chứng minh rằng (SAB) // (ILC) và (SCD) // (BIK).
Phương pháp giải - Xem chi tiết
Nếu mặt phẳng (P) chứa 2 đường thẳng cắt nhau a, b và a, b cùng song song với mặt phẳng (Q) thì (P) song song với (Q).
Lời giải chi tiết
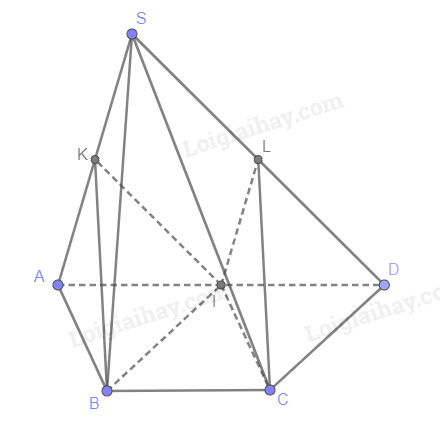
Xét tam giác SAD có I, L lần lượt là trung điểm của AD, SD nên IL // SA. Suy ra IL // (SAB) (1)
AD = 2BC mà I là trung điểm AD nên AI = BC, AI // BC (do ABCD là hình thang). Suy ra AICB là hình bình hành
\( \Rightarrow \)IC // AB \( \Rightarrow \)IC // (SAB) (2)
Từ (1) và (2) suy ra (ILC) // (SAB)
Xét tam giác SAD có I, K lần lượt là trung điểm của AD, SA nên IK // SD. Suy ra IK // (SCD) (3)
AD = 2BC mà I là trung điểm AD nên ID = BC, ID // BC (do ABCD là hình thang). Suy ra BIDC là hình bình hành
\( \Rightarrow \)BI // CD \( \Rightarrow \)BI // (SCD) (4)
Từ (3) và (4) nên (BIK) // (SCD).
Các bài khác cùng chuyên mục
- Bài 4.20 trang 114 SGK Toán 11 tập 1 - Cùng khám phá
- Lý thuyết Công thức nhân xác suất - SGK Toán 11 Cùng khám phá
- Lý thuyết Công thức cộng xác suất - SGK Toán 11 Cùng khám phá
- Lý thuyết Thể tích khối lăng trụ, khối chóp và khối chóp cụt đều - SGK Toán 11 Cùng khám phá
- Lý thuyết Khoảng cách - SGK Toán 11 Cùng khám phá
- Lý thuyết Công thức nhân xác suất - SGK Toán 11 Cùng khám phá
- Lý thuyết Công thức cộng xác suất - SGK Toán 11 Cùng khám phá
- Lý thuyết Thể tích khối lăng trụ, khối chóp và khối chóp cụt đều - SGK Toán 11 Cùng khám phá
- Lý thuyết Khoảng cách - SGK Toán 11 Cùng khám phá
- Lý thuyết Hai mặt phẳng vuông góc - SGK Toán 11 Cùng khám phá













Danh sách bình luận